ORB-SLAM策略思考之RANSAC

1. 初始化器的RANSAC

1. ORB-SLAM中的初始化器是一个端到端的地图初始化策略，即不需要人的参与
2. 双线程同时计算本质矩阵和单应性矩阵
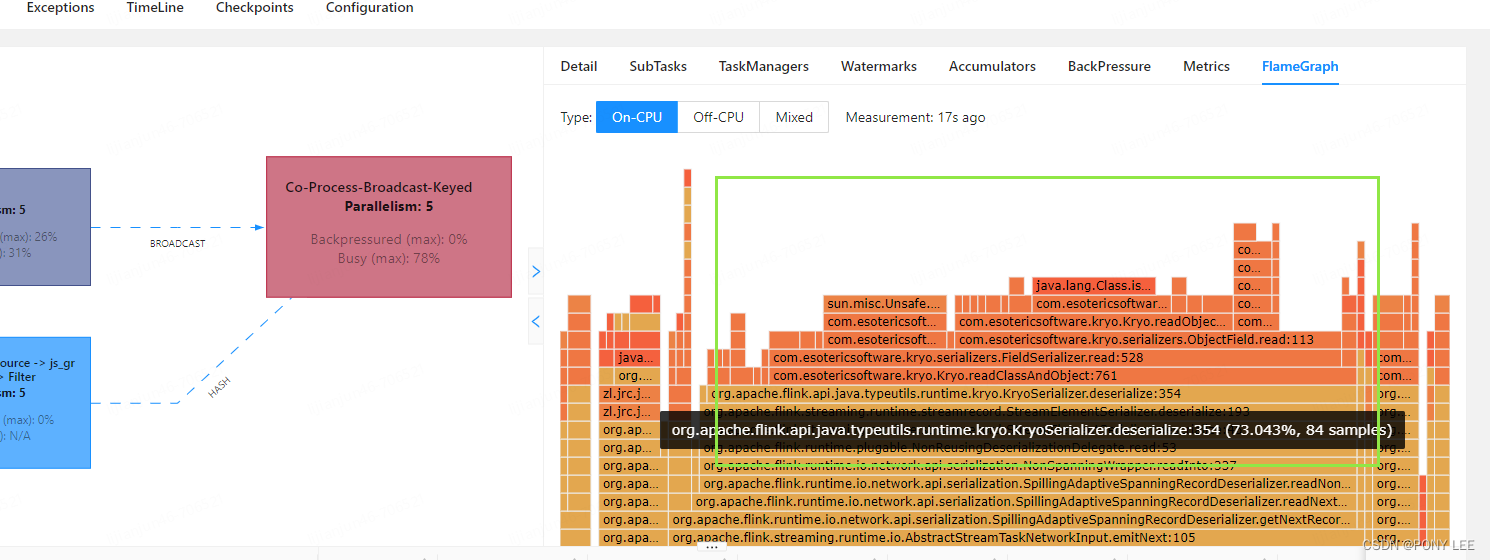
3. 使用基于RANSAC和卡方检验的评价方法
   1. 为了保证两种算法评价的一致性，计算本质矩阵F和单应性矩阵H都采用统一的8点法、5.991卡方值和相同的RANSAC迭代次数。
   2. 对每次RANSAC迭代，进行最佳得分对应的变换矩阵、内点位置进行统计。
   3. 这里的评级方法为：
      1. 使用8点法计算变换矩阵
      2. 计算出变换矩阵后，对所有匹配成功的点进行基于该变换矩阵的重投影，利用卡方检验值进行内点判断
         1. 计算H矩阵时，使用5.991作为内点判断阈值
         2. 计算F矩阵时，使用3.841作为内点的判断阈值
      3. 对判断为内点的匹配，以5.991-重投影距离作为该内点的得分，并进行累计统计
   4. 针对相同的RANSAC迭代算法后，H矩阵和F矩阵都得到了最优得分、对应的内点位置和对应的变换矩阵
4. 变换矩阵选择策略：
   1. 在ORB-SLAM中，并不会直接选择得分最高的匹配思路，而是通过一定的计算方法
   2. 计算H矩阵得分占总分数比例，如果大于0.4，选择H矩阵，否则选择F矩阵
5. 初始化器的最后，就是对选定的矩阵进行运动分解，获取旋转矩阵和平移向量。

2. PnP求解器的RANSAC

1. 在ORB-SLAM中，使用的PnP求解器是EPnP+RANSAC算法
2. 在ORB-SLAM设置RANSAC参数的时候，内点比例（$\omega$）并不是直接根据传入的参数设置的，而是根据一定的计算方式进行修正
   1. ORB-SLAM中不仅会接收内点比例（$\omega$）参数，还会根据最少能接受内点的数目minInlierNum
   2. 根据2d-3d匹配总数$K$和需要的模型估计参数$S_i$进行比较
      1. 当传入的内点比例$\omega$对应的内点数目$\omega K$小于minInlierNum时，以minInlierNum/K修正当前$\omega$
      2. 进行第一步的修正后，如果内点数目小于$S_i$，以$S_i/K$再次对$\omega$进行修正
3. 也就是说，当匹配的数目$K$较少，$\omega$发生第一种修正时，会产生比较大的内点比例，造成的结果就是迭代次数$N$非常小
4. 在跟踪线程的重定位过程中，就是根据迭代次数$N$是否大于5来确定这次的匹配的数目是否达到要求来判断是否丢弃这个重定位的匹配。在ORB-SLAM中会进行5次的迭代来判断迭代次数是否用完，我认为可以对这部分进行优化，根据要求的minInlierNum和匹配数目进行内点占比的求解，从而可以先求出迭代次数，直接进行判断要比迭代5次快的多

3. Sim3求解器的RANSAC

1. 在ORB-SLAM中，使用的Sim3求解器是根据一篇比较久远的论文和RANSAC结合的方式进行的，论文：Closed-form solution of absolute orientataion using unit quaternions
2. 在ORB-SLAM中，SIM3求解器的使用是在回环闭合线程中的计算当前关键帧和回环闭合候选关键帧之间的SIM3矩阵的。使用的策略和PnP求解器中相同
   1. 先进行RANSAC的5次迭代
   2. 如果没有了可用的迭代次数，丢弃这次匹配
3. 正常来讲，计算出来的迭代次数较少只有一个原因，就是内点比例设置的太高了，与PnP求解器类似的是，内点比例并不是通过给定的参数直接赋值的，而是根据最少能接受的内点数目确定的。当最少接受的内点数目要求的较大时，就会造成迭代次数较少的情况，也就是说产生的匹配并不够。
4. 因此，我的观点还是那样，并不需要进行5次迭代，因为这5次迭代过程中RANSAC算法的迭代次数并没有发生动态的更新，直接根据要求的最少的内点数目和匹配数目进行比较就可以直接确定迭代次数，速度会比较快。