MySQL知识点总结(一)——一条SQL的执行过程、索引底层数据结构、一级索引和二级索引、索引失效、索引覆盖、索引下推
- 一条SQL的执行过程
- 索引底层数据结构
- 为什么不使用二叉树?
- 为什么不使用红黑树?
- 为什么不使用hash表?
- 为什么不使用b-tree?
- 一级索引和二级索引
- 索引失效
- 索引覆盖
- 索引下推
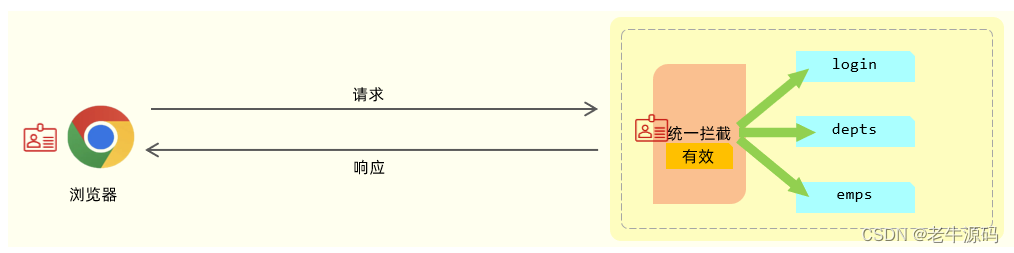
一条SQL的执行过程

- 客户端:用于向服务端发起sql查询或更新请求,MySQL自带的命令行客户端、MySQL的JDBC客户端等都是。
- 连接器:用于接收客户端的连接,并进行身份认证、查询当前账号拥有的权限。
- 查询缓存:MySQL服务端会将一条SQL的查询结果缓存缓存起来,下一次再执行相同的sql时,就可以直接从缓存中取。但是一旦对应的库表发生了更新,缓存将会被清空,因此只适用于更新频率不高的场景,MySQL8.0以上的版本已经将其去除。
- 分析器:对SQL进行词法分析和语法发现,就是分析我们的这个SQL要干啥。
- 优化器:对我们的SQL进行优化,选取使用的索引,生成执行计划。
- 执行器:调用执行引擎的接口进行SQL查询或更新。
索引底层数据结构
MySQL索引的底层数据结构是B+树。
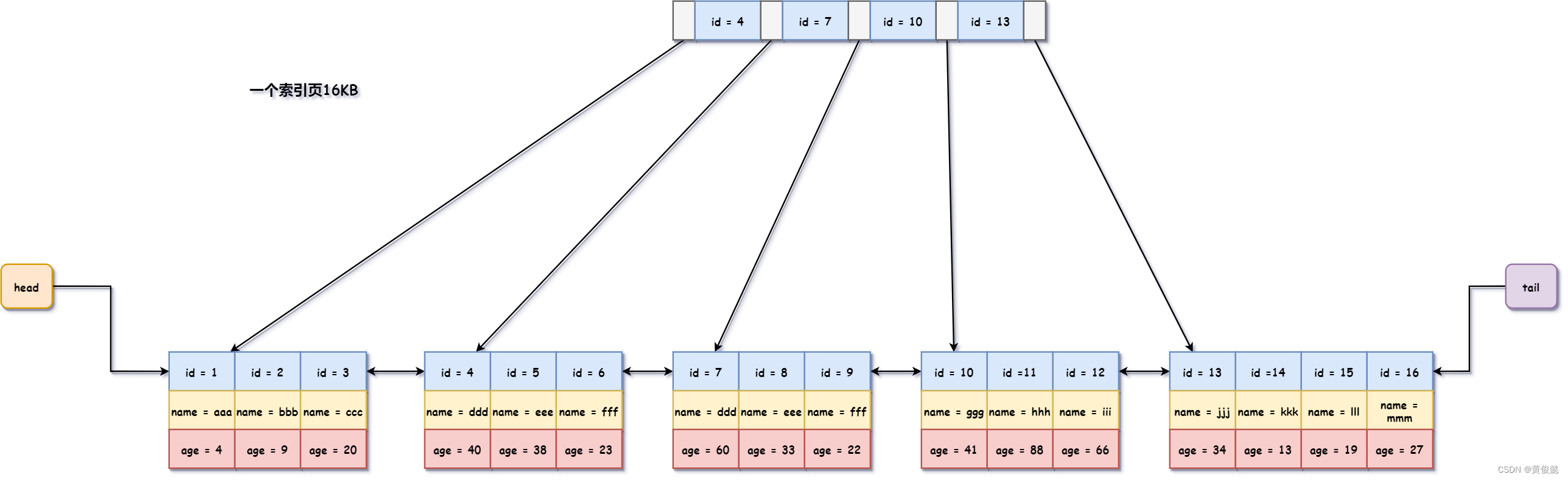
B+树是多路平衡树(B-tree)的一个变种,非叶子节点只存放主键和到下一级节点的指针,叶子节点存放主键和主键对应的数据行记录,叶子节点通过指针进行连接,形成一个双向链表,还有一个头指针和尾指针分别指向链表头节点和尾节点。在MySQL的b+tree中,一个索引页是16KB。
为什么不使用二叉树?
首先我们要明白一点,MySQL中的索引页是存储在磁盘中的,每次读取一个索引页,都是一次磁盘读取,会有磁盘寻址的开销,因此MySQL应该选取一种数据结构,可以让它尽量少的去读取磁盘,才适合作为存储索引的数据结构。
因为二叉树每个节点只有两个出路,树高较高,而B+树是多路平衡树,每个节点有多个出路,树高较矮,这意味着如果用二叉树作为索引的数据结构的话,磁盘寻址的次数会比使用B+树时多,性能不如B+树。
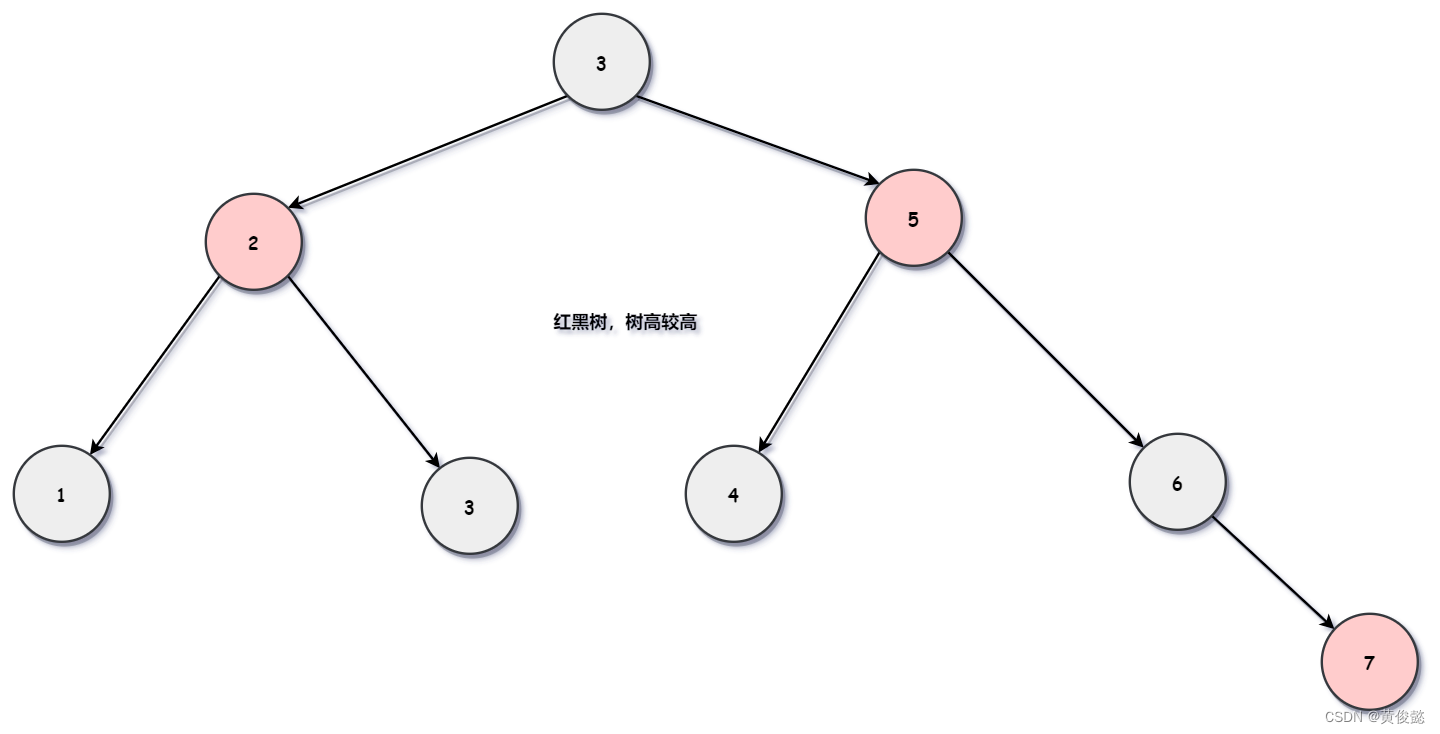
并且,在极端情况下,二叉树会退化成链表,比如id等于1、2、3、4、5、6、7的七条数据按顺序插入,最终二叉树的结果就变成了下图这个样子。
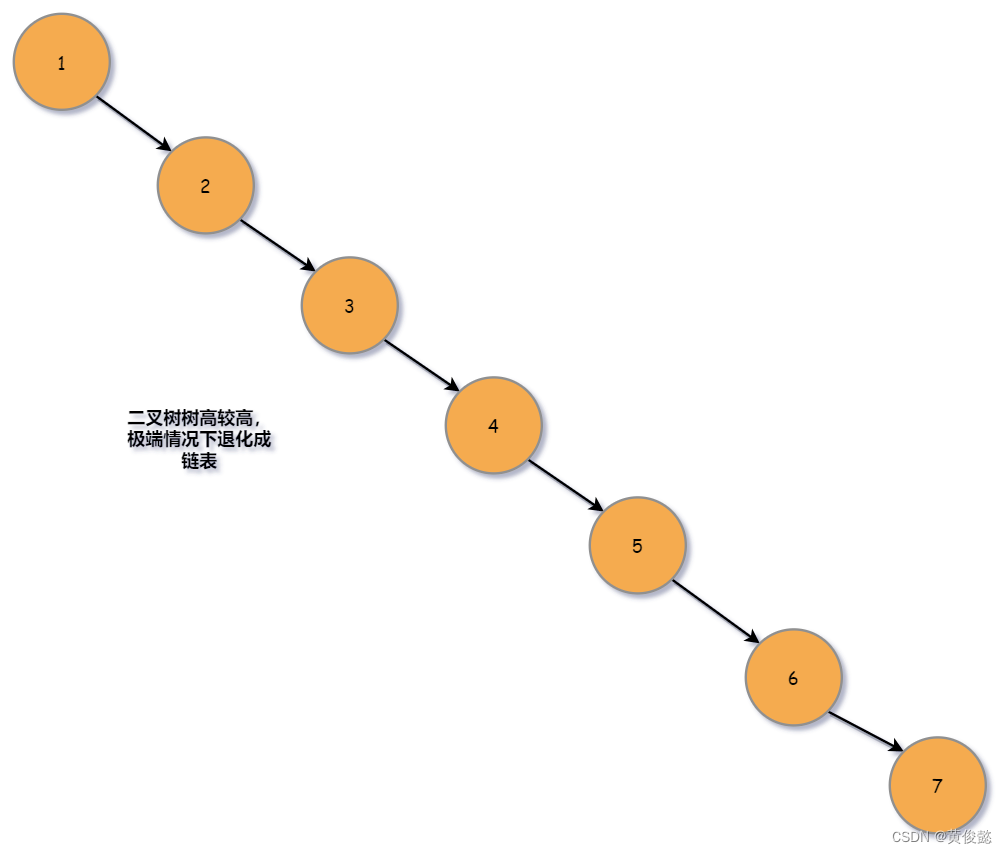
为什么不使用红黑树?
红黑树解决了二叉树极端情况退化成链表的问题,但是它没有解决树高较高的问题,因为红黑树也是一个二叉树的数据结构。
为什么不使用hash表?
hash表在插入和等值查询时非常快,可以做到O(1)的时间复杂度。但是hash表的原理是通过hash函数根据key算出一个hash值,然后通过hash值与hash表中的数组长度取模后,进行散列存储的,数据之间不存在顺序性,因此做索引范围查询时需要进行全表扫描,性能是比较低的。
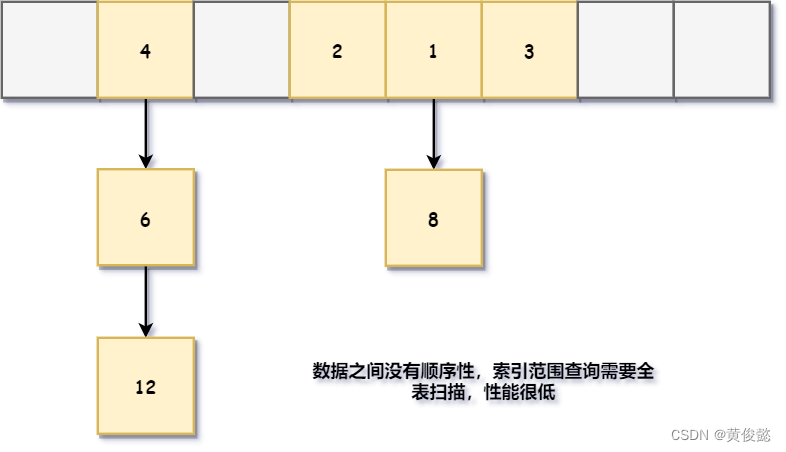
而B+树是按顺序排好序的,并且索引页之间有双向指针,还有头指针和尾指针,范围查询非常方便。
为什么不使用b-tree?
B树是多路平衡树,分叉比二叉树和红黑树多,因此树高会比二叉树和红黑树矮。但是B树的非叶子节点也存放数据,而MySQL的索引页又固定是16KB,因此节点分叉较B+树少,树高比B+树高。此外,B树的叶子节点是没有双向链表连接的,因此范围查询的性能不如B+树。
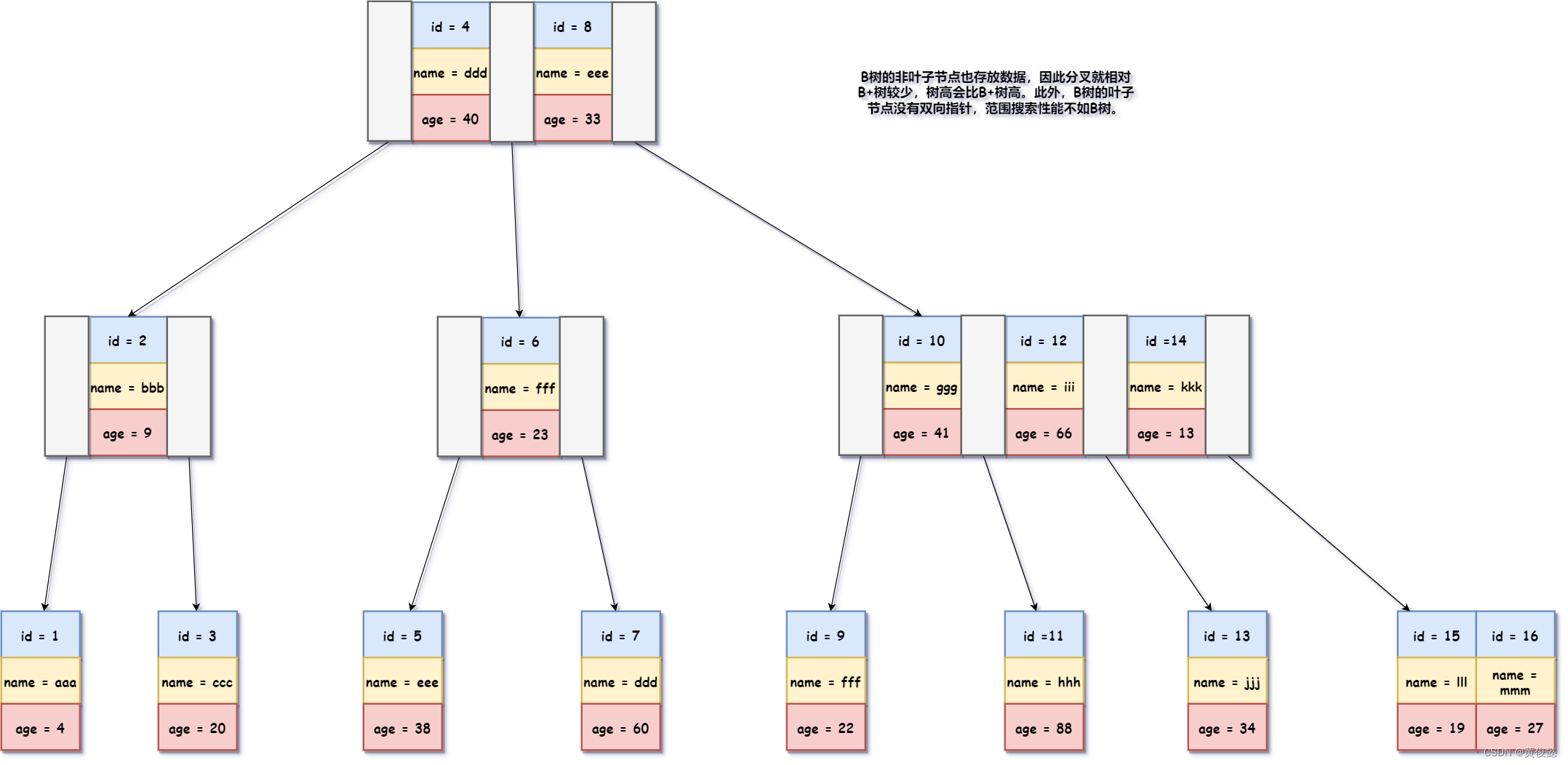
一级索引和二级索引
一级索引也叫主键索引,是以主键作为索引键的索引,在B+树中通过主键进行排序。

二级索引是非主键索引,是以非主键的字段作为索引键进行排序,比如我们以上面的表为例,在age字段上建立一个二级索引,则效果如下图。
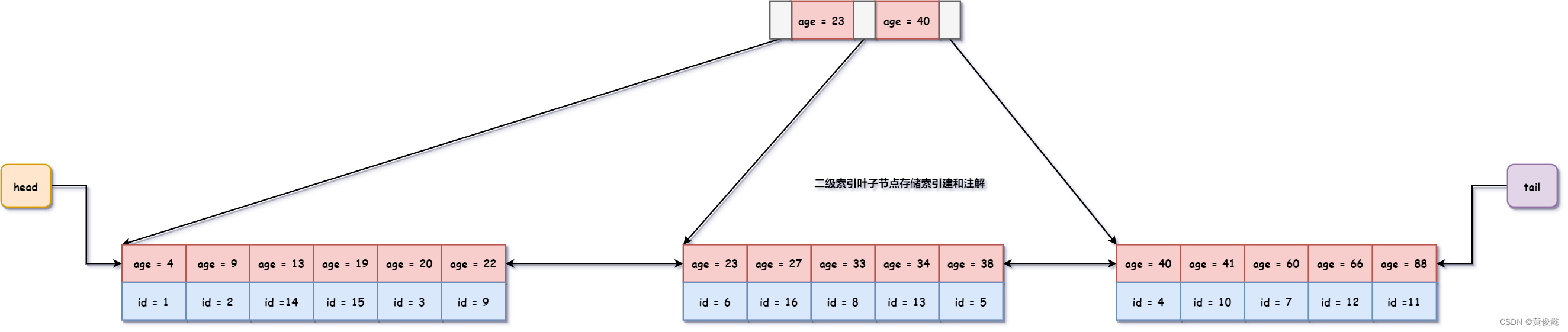
二级节点的叶子节点不存储行记录,而是存储索引建(age字段)和主键(id),当通过二级索引进行搜索时,会先从二级索引找到对应的主键,再通过主键在一级索引中进行查找,这个过程叫做回表。比如我们要通过二级索引查找age=60的这一条数据,则整个过程如下。
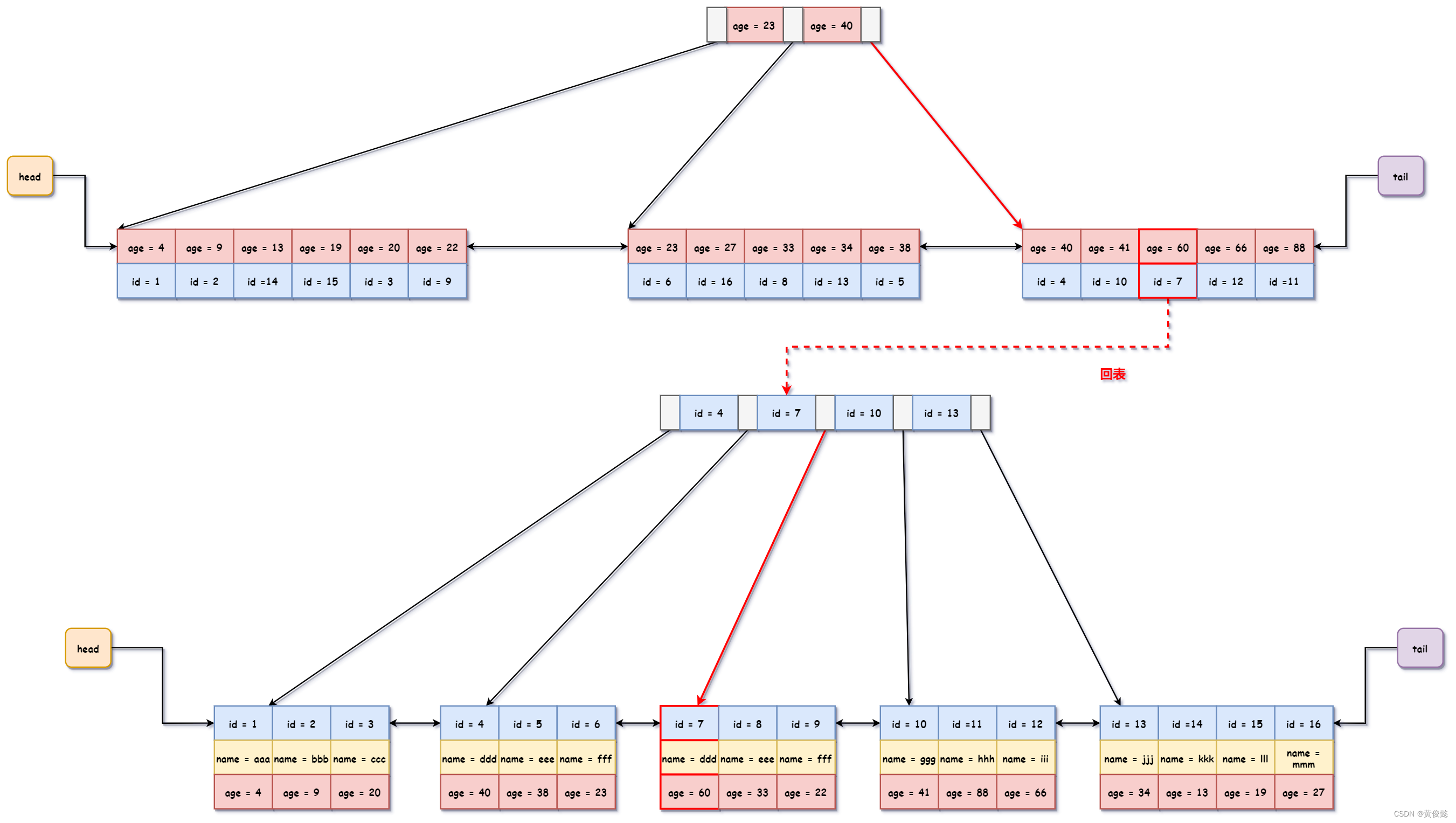
这个回表的过程是有性能开销的,如果MySQL判断走二级索引的代价比较大,不如全表扫描,就会放弃二级索引进行全表扫描。回表一般是因为我们建立二级索引时只包含一个索引键,没有包含要查询的其他字段,如果我们建立二级索引时,连同其他需要查询返回的字段一起建立一个二级联合索引,使得需要查询返回的字段在二级索引叶子节点中都有,MySQL就不会回表,这时候二级索引一般都会生效。
索引失效
索引失效是指由于SQL语句编写不规范(或其他原因)导致MySQL不走已经建立的索引进行查询,以下几种情况都会造成索引失效。
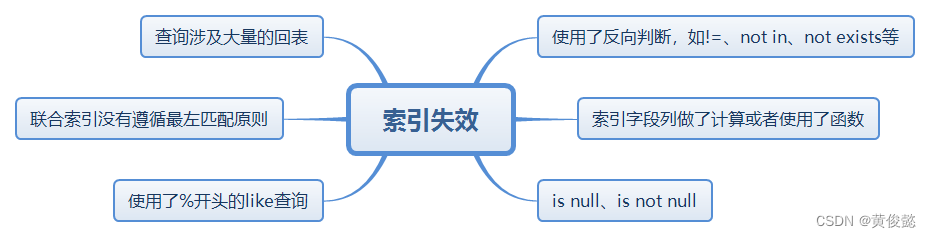
索引覆盖
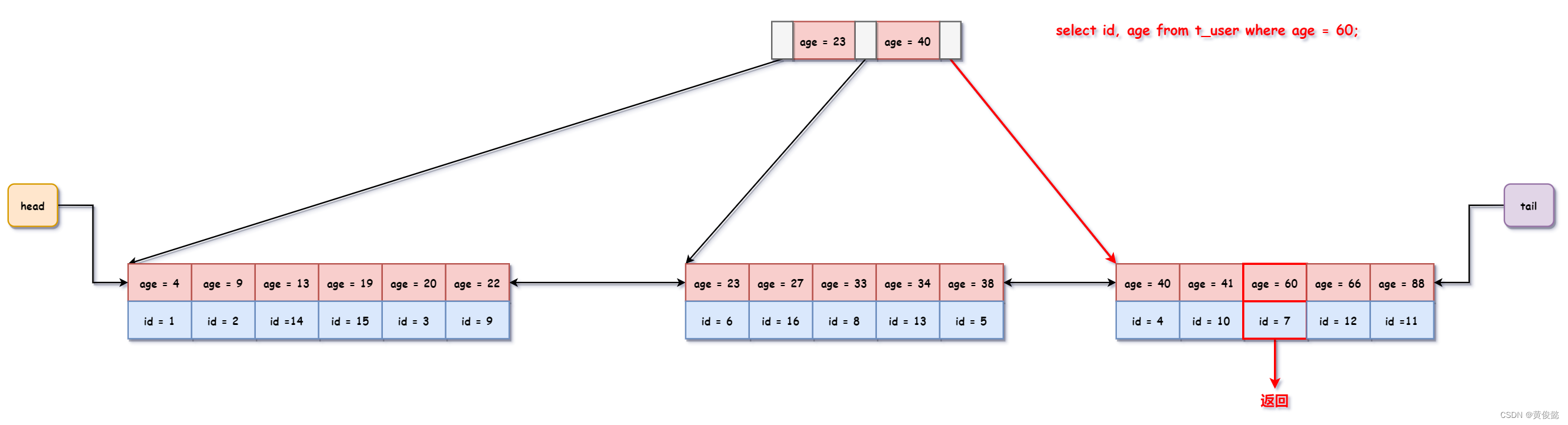
索引覆盖是一种优化二级索引回表查询的手段,在建立索引时,原先的索引键连同最终需要查询返回的字段一起组成一个联合索引。这样,MySQL通过二级索引进行查询时,发现二级索引的叶子节点已经包含了所有需要查询返回的字段,就不会再回表查询,这样查询性能就会大大提高,原本由于大量回表而导致二级索引失效,通过这种优化手段,会使得MySQL会选择这个二级索引进行查询。
索引下推
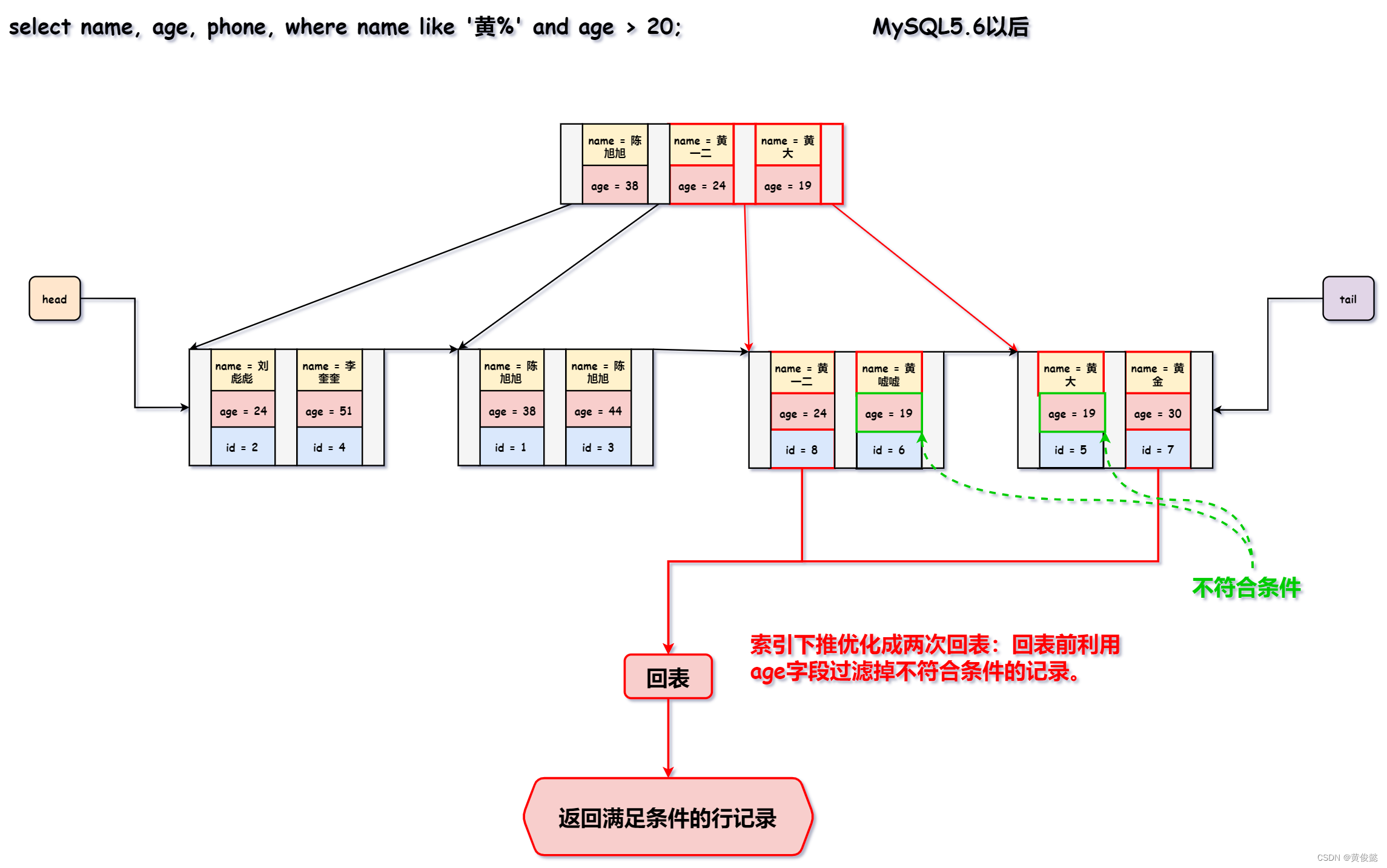
在老版本的MySQL中,如果联合索引查询使用了范围查询,会使得联合索引中范围查询的字段的后续字段失效。比如我们有一张t_user表,有四个字段:“id(主键)、name、age、phone”。现在我们有一个sql:“select name, age, phone, where name like ‘黄%’ and age > 20;”。我们建立了一个联合索引(name,age),如果MySQL查询走了这个索引,那么MySQL5.6以前的版本是这样的:
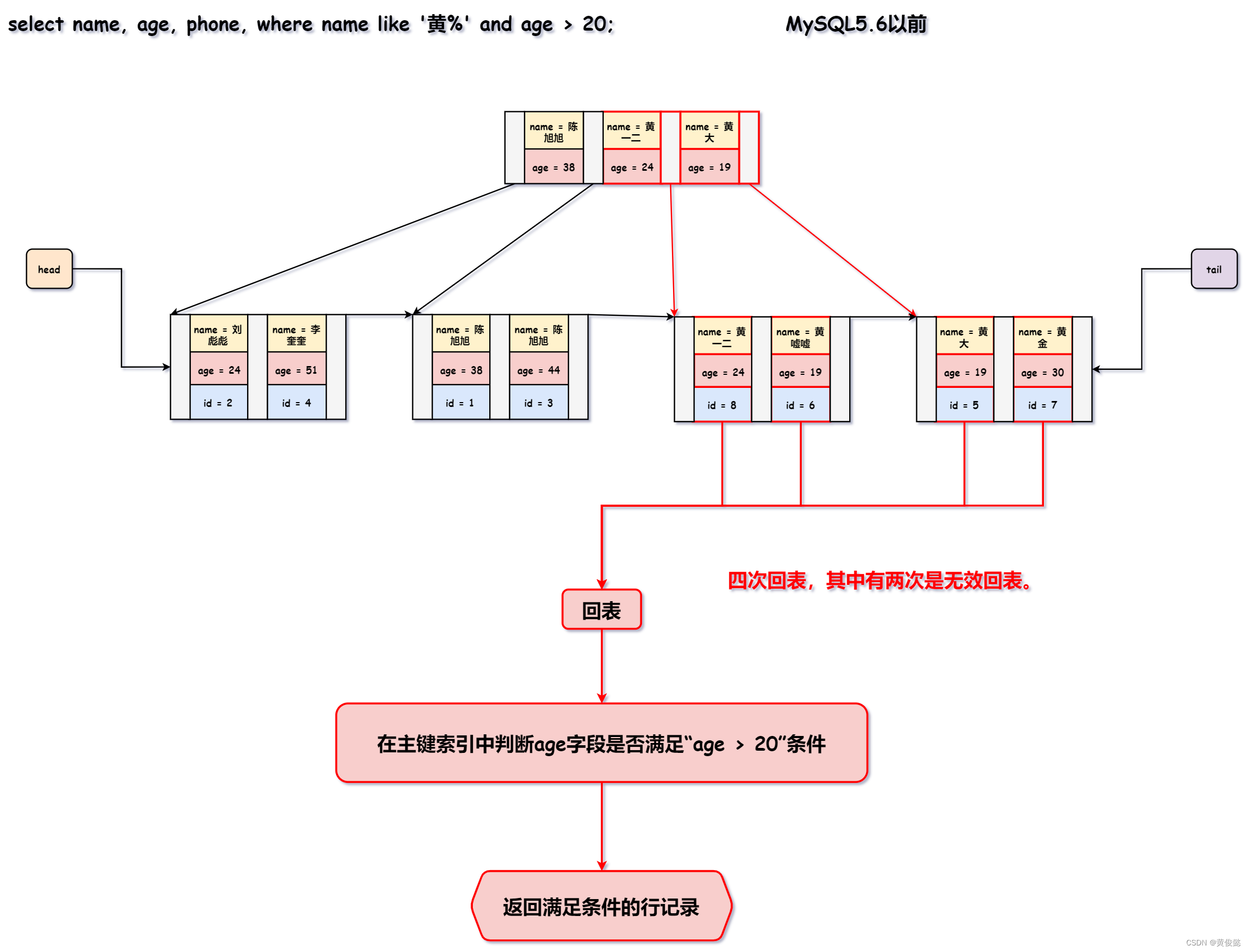
新版本(5.6之后)的MySQL则通过索引下推进行优化,MySQL在通过二级索引中的name字段进行模糊匹配查询后,会利用二级索引中的第二个字段age进行条件判断来做进一步的筛选过滤,过滤掉不满足“age > 20”这个条件的id,这样可以减少回表的次数提升查询性能。