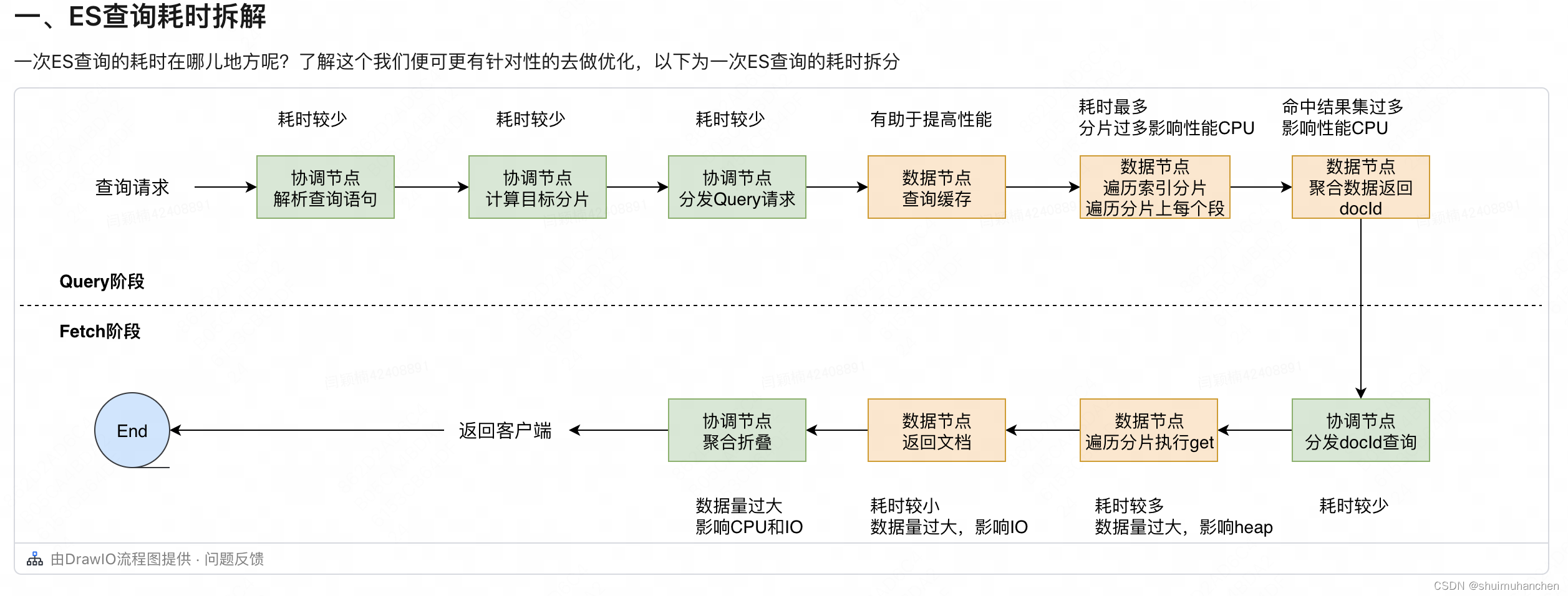
数据变换
- 对数变换
- 傅里叶变换
- Box-Cox 变换
对数变换
对数变换是一种常见的数据变换方法,它将原始数据取对数,常用的是自然对数(以 e 为底)或者以 10 为底的对数。对数变换的作用包括:
- 降低数据的尺度:对数变换可以将原始数据的幅度大幅缩小,使得数据更加集中在一个较小的范围内,有助于减小数据的波动性。
- 减小数据的偏度:对数变换可以有效地处理偏态分布的数据,特别是右偏分布(正偏态),将其转换为更接近于正态分布的形式。
- 稳定方差:对数变换可以减小数据的方差,使得数据的波动更加稳定,有利于后续的建模和分析。
举例来说,假设我们有一个包含房屋价格的数据集,通常情况下,房屋价格是右偏分布的,即大部分房价集中在较低的范围内,但存在少量极高的房价。这时可以对房价数据进行对数变换,将其转换为对数价格,这样可以使得价格的波动更加平缓,同时也使得模型更容易捕捉到价格之间的差异。
正态分布与偏态分布:
- 正态分布:平均数=中位数=众数
- 正偏态分布:平均数>中位数>众数
- 负偏态分布:平均数<中位数<众数
偏态分布的数据有时取对数后可以转化为正态分布,反映偏态分布的集中趋势往往用中位数。
正偏态与负偏态的形状如下图所示:

log 函数的曲线如下图所示:


傅里叶变换
傅里叶变换(Fourier Transform)是一种将一个信号从时域(时间域)转换到频域(频率域)的数学方法。它可以将一个信号表示为一些正弦波和余弦波的线性组合,这些正弦波和余弦波被称为频率分量或谐波。
傅里叶变换的定义是:
F
(
w
)
=
∫
−
∞
∞
f
(
t
)
e
−
j
w
t
d
t
F(w) = \int_{-\infty }^{\infty }f(t)e^{-jwt}dt
F(w)=∫−∞∞f(t)e−jwtdt
其中,
f
(
t
)
f(t)
f(t) 是输入信号,
F
(
w
)
F(w)
F(w) 是信号在频率域中的表示,
w
w
w 是角频率,
j
j
j 是虚数单位。
傅里叶变换将一个复杂的时域信号拆解成若干个简单的频域信号,每个频域信号都对应着输入信号中不同的频率成分,并给出了该频率成分的权重和相位信息。因此,傅里叶变换可以用于分析信号中的频率成分,并在频域中对信号进行滤波、降噪等处理。
傅里叶变换有两个常见的变种:离散傅里叶变换(DFT)和快速傅里叶变换(FFT)。离散傅里叶变换是傅里叶变换在离散时间下的表示形式,它是傅里叶变换在计算机上应用最为广泛的形式。快速傅里叶变换则是一种高效的算法,用于计算离散傅里叶变换,可以大幅提高计算效率。
傅里叶变换是一种重要的数学工具,广泛应用于信号处理、图像处理、通信、物理学、工程学等领域。
Box-Cox 变换
Box-Cox 变换是一种常用的数据变换方法,用于处理数据的非正态分布或异方差性。它通过对数据进行幂函数变换来使其满足正态分布或减小异方差性。
Box-Cox变换的一般形式为:
y
(
λ
)
=
{
(
x
λ
−
1
)
/
λ
λ
≠
0
l
o
g
(
x
)
λ
=
0
y(\lambda ) = \left\{\begin{matrix}(x^\lambda - 1) / \lambda & \lambda \neq 0 \\ log(x) & \lambda = 0 \end{matrix}\right.
y(λ)={(xλ−1)/λlog(x)λ=0λ=0
其中,
x
x
x 表示原始数据,
y
(
λ
)
y(\lambda )
y(λ) 表示经过 Box-Cox 变换后的数据,
λ
\lambda
λ 是控制变换程度的参数。
当 λ \lambda λ 的取值不同时,Box-Cox 变换可以实现不同的效果:
- 当 λ \lambda λ 等于 1 时,Box-Cox 变换退化为简单的线性变换。
- 当 λ \lambda λ 接近 0 时,Box-Cox 变换可近似为对数变换,适用于数据右偏且存在较大的正值。
- 当 λ \lambda λ 大于 1 时,Box-Cox 变换可将数据向左偏斜转换为正态分布。
- 当 λ \lambda λ 小于 1 时,Box-Cox 变换可将数据向右偏斜转换为正态分布。
举例来说,假设我们有一个包含正值和负值收入的数据集,我们希望将其转换为正态分布,那么可以使用 Box-Cox 变换来实现这个目标。首先,我们选择合适的 λ \lambda λ 值,例如 λ = 0 \lambda=0 λ=0;然后应用 Box-Cox 变换公式,对数据集中的每个值进行变换;经过变换后的数据将更接近正态分布。
另一个例子是在回归分析中使用 Box-Cox 变换来处理异方差性。当回归模型中存在异方差时,我们可以通过应用 Box-Cox 变换来减小误差的方差,从而提高模型的拟合效果。
异方差性(Heteroscedasticity)是指在回归分析中,随着自变量的变化,因变量的方差不是常数,而是具有一定的变化趋势。也就是说,不同的观测值对应的误差方差不同。
异方差性通常会导致回归模型不准确,不可靠甚至是无效的。因为回归模型的基本假设之一是误差项的方差是恒定的,如果出现异方差性,那么这个假设就不再成立了。
异方差性在回归模型中出现的原因可能有多种,包括:
- 数据采集过程中存在系统误差,例如测量误差、观测误差等。
- 因变量的方差与自变量之间存在某些联系,例如经济学中研究收入与支出的关系,高收入人群的支出方差可能比低收入人群更大。
- 模型本身的限制和假设不足,例如使用线性模型描述非线性关系、忽略未知的重要解释变量等。




![[BUUCTF 2018]Online Tool(特详解)](https://img-blog.csdnimg.cn/img_convert/77e34e7e79cd1578ee5a5c64480b4e76.png)