P11 PyTorch Momentum

news2025/11/1 6:36:38

参考：

关于梯度下降与Momentum通俗易懂的解释_ssswill的博客-CSDN博客_梯度 momentum

前言：

P9讲梯度的时候，讲到过这种算法的梯度更新方法

这边重点讲解一下原理

Momentum算法又叫做冲量算法，其迭代更新公式如下：

$v_t= \beta v_{t-1}+(1-\beta)\bigtriangledown w$

$w_{t}=w_{t}-\alpha v_{t}$

实验表明，相比于标准梯度下降算法，Momentum算法具有更快的收敛速度

1：标准的梯度下降问题(w维度为1）

2：标准的梯度下降问题(W维度为2）

3： Momentum

一标准的梯度下降问题(w维度为1）

$w_t=w_t-\alpha \bigtriangledown w$

# -*- coding: utf-8 -*-
"""
Created on Tue Jan  3 21:48:15 2023

@author: cxf
"""

import numpy as np
import matplotlib.pyplot as plt


#计算梯度
def gradient(x):
    return 2*x


'''
a: 搜索的起始点
step: 步伐
epoch: 迭代次数
'''
def gradient_descent(a, step, epoch):
    
     x = a
     for i in range(epoch):
         
         grad = gradient(x)
         x = x-step*grad
         
         print('epoch:{},x= {},gradient={}'.format(i,round(x,3),round(grad,3)))
         
         if abs(grad)<1e-6 :
             return x
     return x

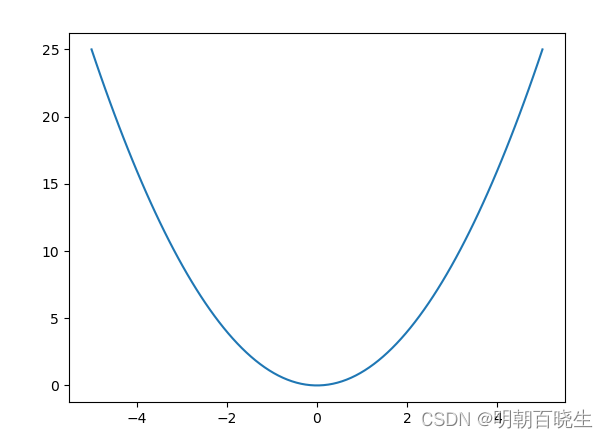
if __name__ == "__main__":
    x = np.linspace(-5,5,100)
    y = x**2 #损失函数
    
    plt.plot(x,y)
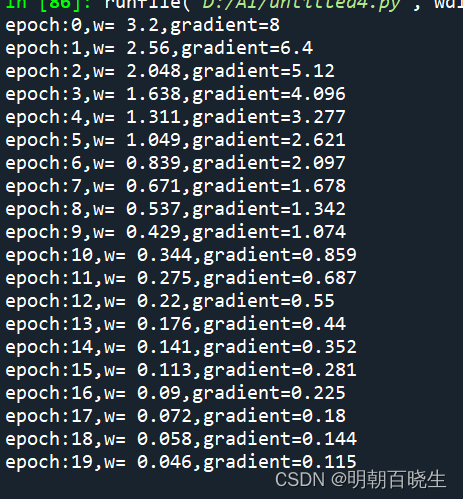
    gradient_descent(4, 1.0,20)

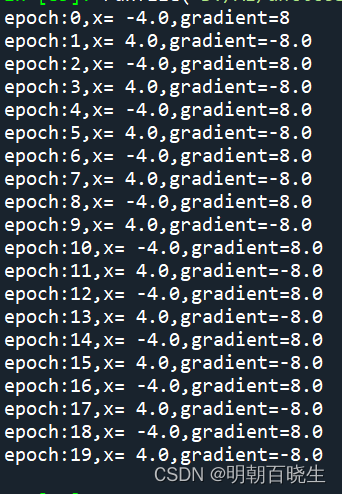
1.1 学习率过小, 却使得学习过程过于缓慢

gradient_descent(4, 0.1,20)

1.2 学习率过大,无法收敛,发散

gradient_descent(4, 1.0,20)

二标准的梯度下降问题(W维度为2）

假设权重系数为

$w=[w_0,w_1]$

假设损失函数

$l=w_0^2+50*w_1^2$

则

$\triangledown w= [2*w_0,100*w_1]$

SGD 更新过程

$w=w-\alpha \bigtriangledown w$

问题：

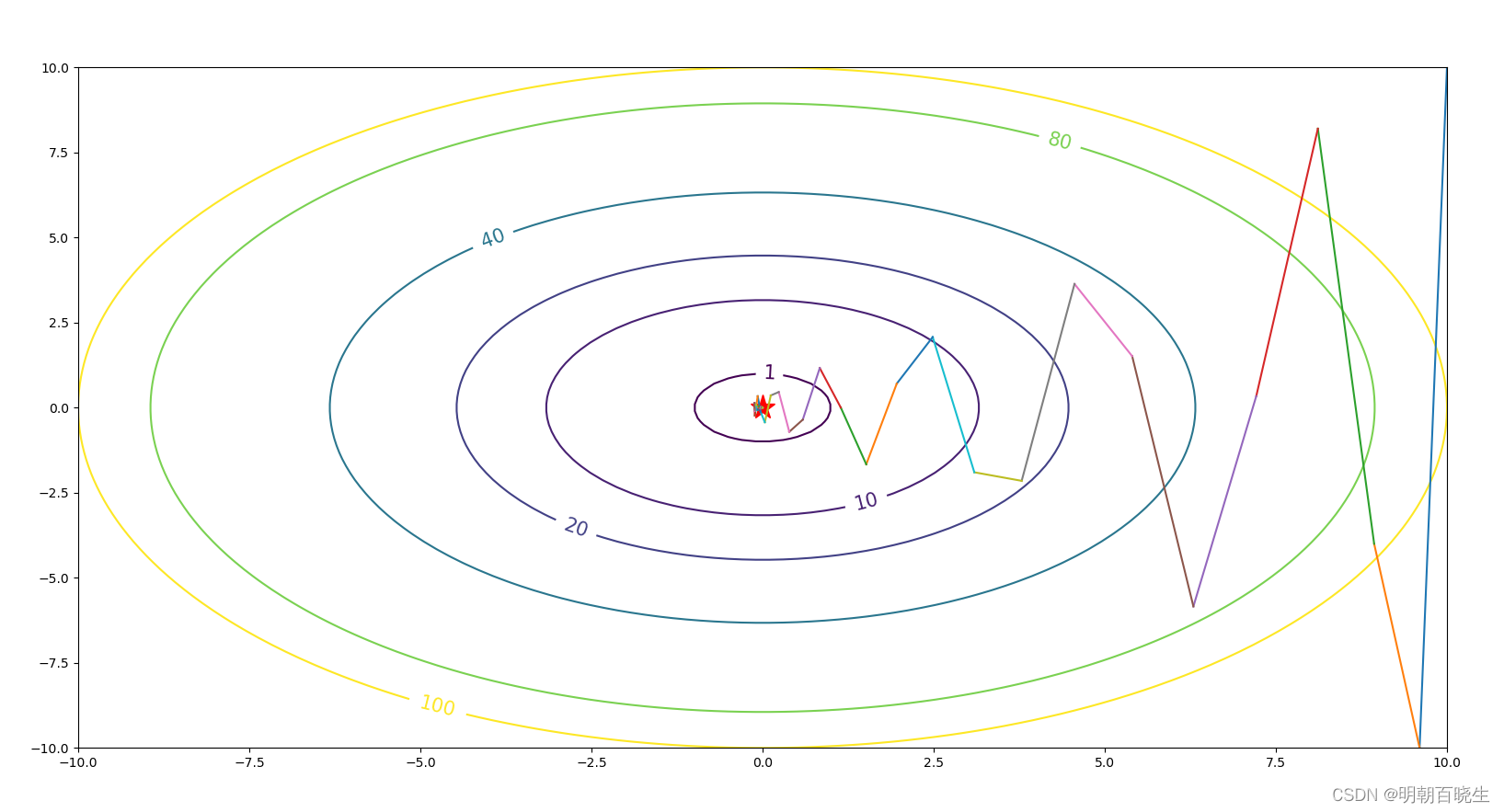
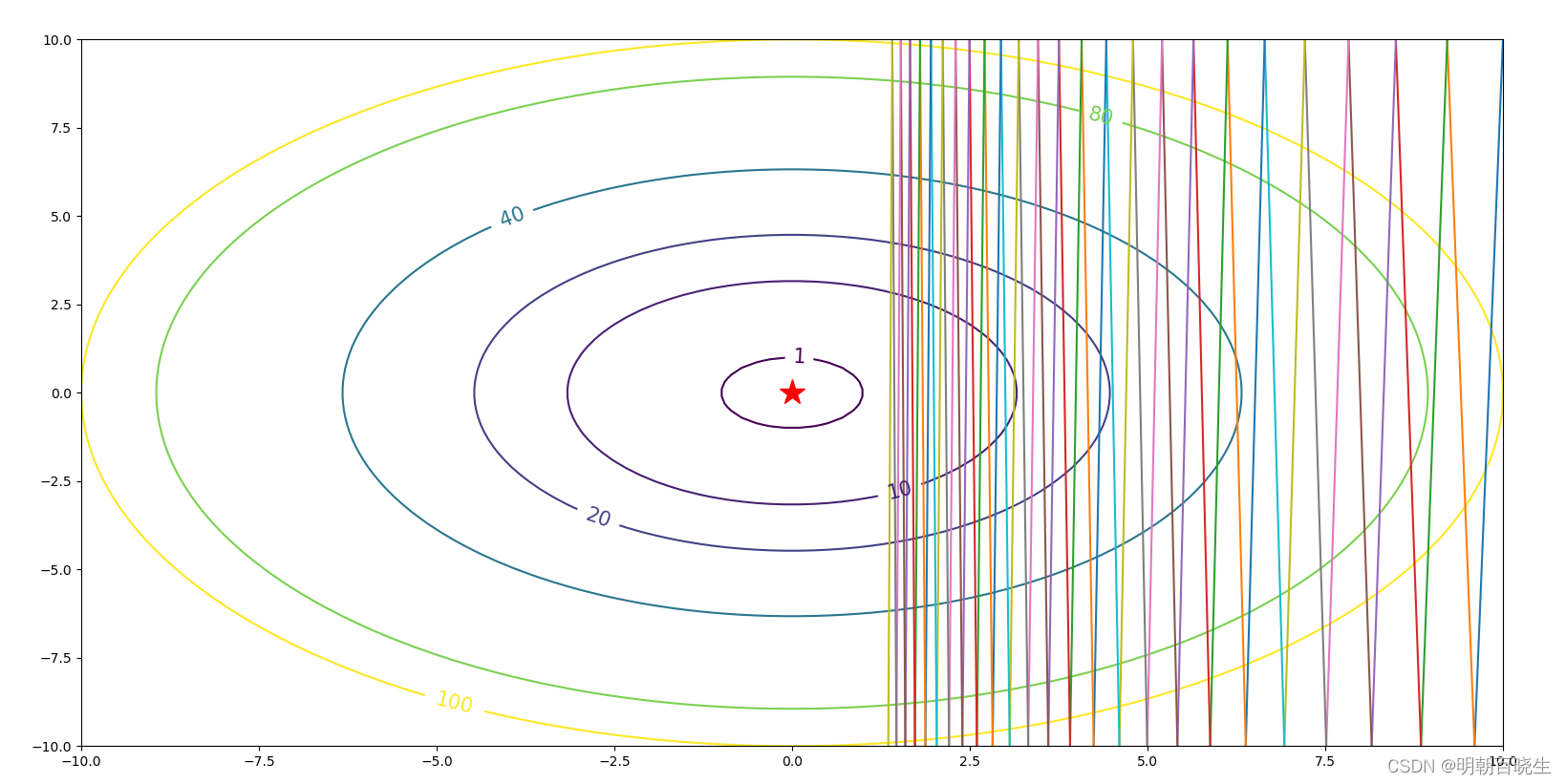
红线是标准梯度下降法，可以看到收敛过程中产生了一些震荡。这些震荡在纵轴方向上( $w_1$ )是均匀的，几乎可以相互抵消，也就是说如果直接沿着横轴方向迭代，收敛速度可以加快

对应的代码

# -*- coding: utf-8 -*-
"""
Created on Wed Jan  4 20:41:03 2023

@author: cxf
"""

import numpy as np
import pylab as plt



'''
显示等高线
'''
def  get_contour():
      w0 = np.linspace(-10, 10,100)
      w1 = np.linspace(-10, 10,100)
      X,Y = np.meshgrid(w0,w1)
      Z = X**2+Y**2
      
      return X,Y,Z
      
      
      
'''
计算梯度
'''
def gradient(w):
    
    w = np.array(w)
    w0 = w[0]
    w1 = w[1]
    grad = np.array([2*w0,100*w1])
    return grad



'''
w: 相当于权重系数
step: 步伐
epoch: 迭代次数
'''
def SGD(w,step,epoch):
    
    w = np.array(w,dtype='float64')
    w_list=[]
    
    for i in range(epoch):

        t = w.copy()
        w_list.append(t)
        grad = gradient(w)
        
        
        print('epoch: %d  权重系数x: [%5.3f   %5.3f]  梯度 [%5.3f  %5.3f ] '%(i,w[0],w[1],grad[0],grad[1]))
        w= w- step*grad
        if sum(abs(grad))<=1e-6:
            return w
    return w,w_list

'''
'''
def momentum(w0, step,mu, epoch):

     w = np.array(w0)
     w_list = []
     
     pre_gd = np.array([0,0])
     for i in range(epoch):
         
         t = w.copy()
         w_list.append(t)
         grad = gradient(w)
         pre_gd = mu*pre_gd+grad
         
         w = w- step*pre_gd
      
         print('epoch: %d  权重系数x: [%5.3f   %5.3f]  梯度 [%5.3f  %5.3f ] '%(i,w[0],w[1],grad[0],grad[1]))
         if sum(abs(grad))<=1e-6:
             return w
     return w,w_list
         
         
     
      
'''
模拟SGD梯度下降训练的过程
'''
def  main():
    
    X,Y,Z = get_contour()
    plt.figure(figsize=(15,7))
    C= plt.contour(X,Y,Z,[1,10,20,40,80,100])#find_grad
    plt.clabel(C, inline=True, fontsize=15)
    plt.plot(0,0,marker='*',markersize=20,color='r')
    
    mu =0.7
    step = 0.02 #步伐
    epoch = 50 #迭代次数
    w =[10,10] #初始化的权重系数
    #x, x_list = SGD(w, step,epoch)
    x, x_list =  momentum(w, step,mu, epoch)
    N = len(x_list)
    print("\n N",np.shape(x_list))
    for i in range(N-1):
        #print(i)
        plt.plot([x_list[i][0],x_list[i+1][0]],[x_list[i][1],x_list[i+1][1]])
        
      
    
    
if __name__ == "__main__":
    

  
    main()

问题1：steps = 0.015 #步伐 epoch = 50 #迭代次数 w =[10,10] #初始化的权重系数

发现收敛速度很慢

问题2：增大 steps = 0.02

步伐 epoch = 50 #迭代次数
w =[10,10] #初始化的权重系数

$w_1$ 参数震荡，无法收敛