深度强化学习(DRL)
本文是学习笔记,如有侵权,请联系删除。本文在ChatGPT辅助下完成。
参考链接
Deep Reinforcement Learning官方链接:https://github.com/wangshusen/DRL
源代码链接:https://github.com/DeepRLChinese/DeepRL-Chinese
B站视频:【王树森】深度强化学习(DRL)
豆瓣: 深度强化学习
文章目录
- 深度强化学习(DRL)
- ALPHAGO
- High level Ideas
- Initialize Policy Network by Behavior Cloning
- Train Policy Network Using Policy Gradient
- Train the Value Network
- Monte Carlo Tree Search(MCST)
- 第一步——选择(Selection)
- 第二步——扩展 (Expansion)
- 第三步一一求值 (Evaluation)
- 第四步一一回溯 (Backup)
- Decision Making after MCTS
- MCTS: Summary
- Summary
- AlphaGo Zero
- 后记
ALPHAGO
围棋游戏介绍
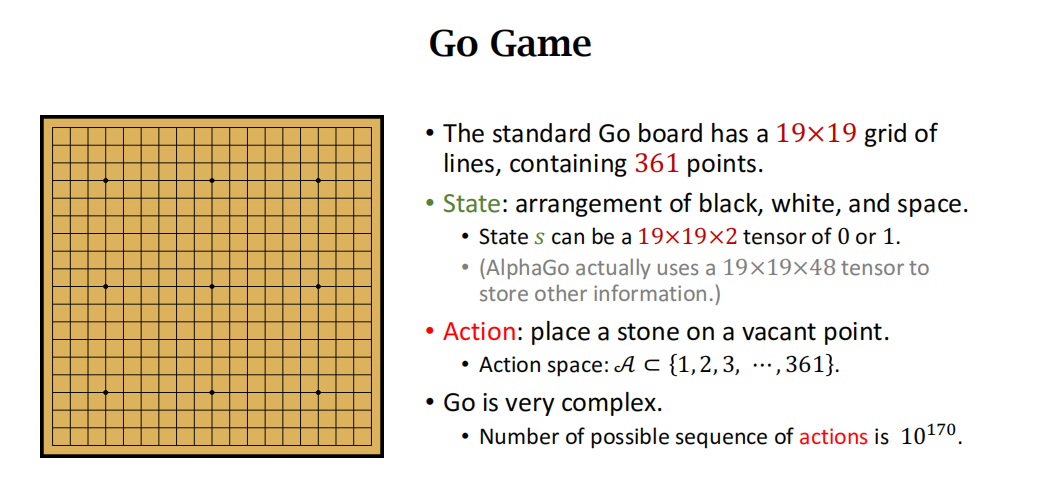
High level Ideas
训练包含3步:
1.用behavior cloning初始化策略网络
2.用策略梯度训练策略网络
3.策略网络训练完之后,用它来训练价值网络。
ChatGPT介绍什么是Behavior cloning:
Behavior cloning(行为克隆)是一种强化学习中的学习方法,其中一个模型(通常是神经网络)被训练来模仿从专家或经验数据中收集的行为,而不是通过试错和奖励信号的方式学习。
具体来说,Behavior Cloning 的步骤通常包括:
-
数据收集: 从一个经验丰富的策略(通常是人类专家)中收集行为数据。这些数据包括状态和相应的行为。
-
模型训练: 使用这些收集到的专家数据来训练一个模型,通常是一个神经网络。模型的目标是学习输入状态与相应的动作之间的映射,以最大程度地模仿专家的行为。
-
评估和部署: 对训练好的模型进行评估,看它在模仿专家行为方面的表现。如果表现良好,可以将该模型部署到实际环境中,让它执行相似的任务。
Behavior Cloning 的优势在于它可以通过直接模仿专家的行为,快速学习复杂的任务,而不需要通过强化学习中的奖励信号进行调整。然而,它的局限性在于如果专家的行为在某些情况下是不完美的,模型也会模仿这些不完美的行为。此外,对于某些复杂的任务,仅仅通过行为克隆可能无法获得鲁棒且高效的策略。
执行(真正和人下棋)的时候:用策略网络和价值网络进行蒙特卡洛树搜索(MCTS)
CahtGPT介绍什么是MCTS:
蒙特卡洛树搜索(Monte Carlo Tree Search,MCTS)是一种用于决策树搜索的概率模型,主要用于解决不确定性和部分可观察性问题。它最初是为解决棋类游戏的人工智能问题而提出的,但后来被扩展应用到各种领域。
MCTS 的核心思想是通过模拟随机采样的方式来估计每个决策节点的值,从而构建一个搜索树,帮助在决策时找到最优的路径。整个搜索过程包括以下四个阶段:
-
选择(Selection): 从树的根节点开始,根据一定的策略选择一个节点,直到达到一个未被完全扩展的节点。
-
扩展(Expansion): 对于选择的节点,根据可行的动作扩展一层节点,选择一个未被访问的子节点。
-
模拟(Simulation): 从扩展的节点开始,使用随机策略或启发式方法模拟若干步,直到达到某个终止状态,得到一个模拟的结果。
-
反向传播(Backpropagation): 将模拟结果反向传播到选择的路径上的所有节点,更新它们的统计信息(例如,访问次数和累积奖励),以帮助更好地估计节点的价值。
这四个阶段不断迭代执行,直到分配给搜索的计算时间达到预定的限制。最终,根据节点的统计信息选择一个最有希望的决策。
MCTS 的一个典型应用是在棋类游戏中,如AlphaGo就使用了变种的 MCTS 算法。然而,MCTS 也可以应用于其他领域,如规划问题和决策问题。

AlphaGo zero的状态
19 x 19 x 17 stack
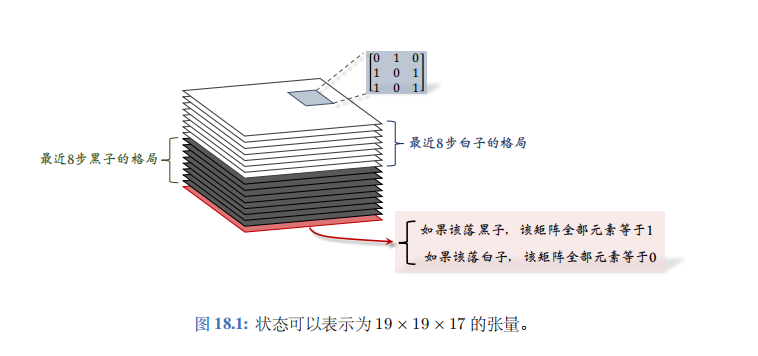
AlphaGo 2016 版本使用 19 × 19 × 48 19\times19\times48 19×19×48 的张量 (tensor) 表示一个状态。AlphaGo Zero 使用 19 × 19 × 17 19\times19\times17 19×19×17 的张量表示一个状态。本书只解释后者;见图 18.1。下面解释 19 × 19 × 17 19\times19\times17 19×19×17 的状态张量的意义。
- 张量每个切片(slice)是 19×19 的矩阵,对应 1 9 × 19 9\times19 9×19 的棋盘。一个 19×19 的矩阵可以表示棋盘上所有黑子的位置。如果一个位置上有黑子,矩阵对应的元素就是1, 否则就是 0。同样的道理,用一个 19×19 的矩阵来表示 当前棋盘上所有白子的位置。
- 张量中一共有 17 个这样的矩阵;17 是这样得来的。记录最近8 步棋盘上黑子的位置,需要 8 个矩阵。同理,还需要 8 个矩阵记录白子的位置。还另外需要一个矩阵表示该哪一方下棋;如果该下黑子,那么该矩阵元素全部等于1;如果该下白子, 那么该矩阵的元素全都等于0。
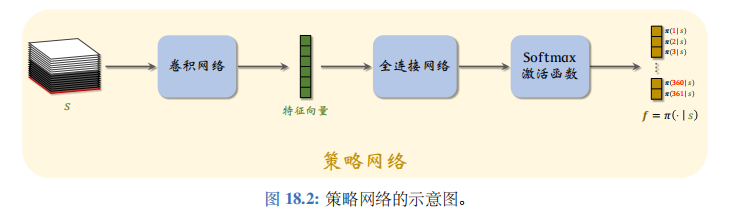
策略网络 π ( a ∣ s ; θ ) \pi(a|s;\boldsymbol{\theta}) π(a∣s;θ) 的结构如图 18.2 所示。策略网络的输入是 1 9 × 19 × 17 9\times19\times17 9×19×17 的状态 s s s。 策略网络的输出是 361 维的向量 f f f, 它的每个元素对应一个动作 (即在棋盘上一个位置放棋子)。向量 f f f 所有元素都是正数,而且相加等于 1。
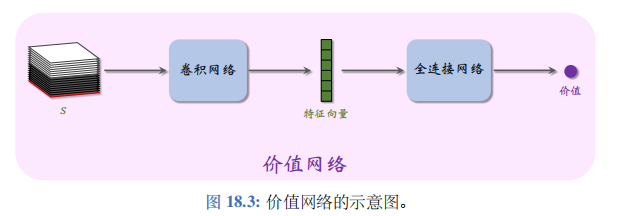
AlphaGo 还有一个价值网络 v ( s ; w ) v(s;w) v(s;w), 它是对状态价值函数 V π ( s ) V_\pi(s) Vπ(s) 的近似。价值网络的结构如图 18.3 所示。价值网络的输入是 19× 19× 17 的状态 s s s。价值网络的输出是一个实数,它的大小评价当前状态 s s s 的好坏
策略网络和价值的输入相同,都是状态 s s s。它们都用多个卷积层把 s s s 映射到特征向量。因此可以让策略网络和价值网络共用卷积层。训练策略网络和价值网络的方法在之后解释。
Initialize Policy Network by Behavior Cloning
从人的记录中学习

用到的是behavior cloning,这不是强化学习,这是模仿学习。模仿学习没有reward。

用棋盘上的动作来看behavior cloning:就是多分类(361个分类,具体指的是下在棋盘的哪个位置),把人类玩家的动作看作是ground truth(真实的标签)
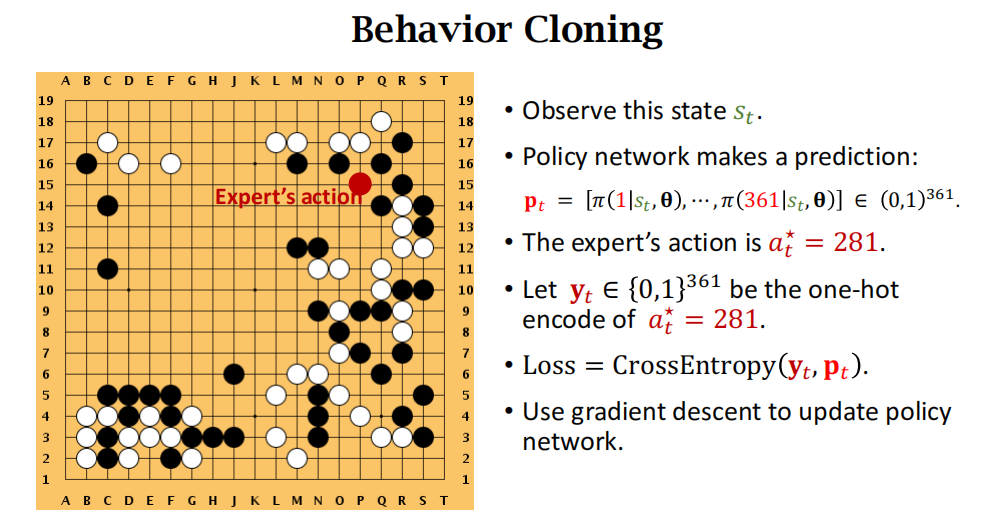
但是behavior cloning存在缺陷,它的效果不如强化学习。
下面是ChatGPT给出的答案:
是的,行为克隆(Behavior Cloning)虽然在某些情境下表现得很好,但也存在一些缺陷和限制:
-
数据分布偏差: 行为克隆是基于专家示范数据的学习方法,如果专家示范的数据不能充分覆盖所有可能的情况,模型在未见过的情况下可能表现不佳。模型只能复制示范的行为,而不一定能够泛化到未知情况。
-
错误传递: 如果专家示范中存在错误的决策或不良策略,行为克隆模型也会学到这些错误。模型无法纠正示范数据中的错误,而是简单地复制了这些错误的决策。
-
缺乏探索: 行为克隆不具备主动探索新的策略的能力。它仅仅复制了专家的行为,而无法在未知环境中进行探索和发现更好的策略。
-
分布变化敏感: 如果环境的分布发生变化,行为克隆模型可能会失效。它对训练时的数据分布敏感,而无法适应新的分布。
-
缺乏理解: 行为克隆模型通常是一个黑盒,无法理解其内部决策过程。这在需要解释和理解模型行为的场景中可能是一个问题。
-
需要大量专家示范数据: 在某些情况下,行为克隆需要大量的专家示范数据才能学到鲁棒的模型。这可能对于一些复杂任务来说是一个挑战,因为获取专家示范数据可能很昂贵或困难。
为了解决这些问题,研究者们提出了许多改进方法,如结合强化学习和自我对弈来引入探索、使用逆强化学习来更好地理解任务目标等。在实际应用中,选择合适的学习方法取决于具体问题的特性和需求。

Train Policy Network Using Policy Gradient
具体怎么用强化学习来训练策略网络呢?AlphaGo让两个策略网络进行博弈,一个叫做Player,另一个叫做Opponent。
Player是agent,它是由策略网络来控制的,用的是策略网络最新的模型参数(每下完一局围棋把胜负作为奖励,靠奖励来更新player的参数)
Opponent相当于environment,它负责陪玩(player下一步棋,opponent跟着下一步),它也是用策略网络来控制的,但是opponent的参数无需学习,随机从旧的策略网络的参数中随机选择一个即可。

让“玩家”和“对手”博弈,将一局游戏进行到底,假设走了 n n n 步。游戏没结束的时候,奖励全都是零:
r 1 = r 2 = ⋯ = r n − 1 = 0. r_{1}\:=\:r_{2}\:=\:\cdots\:=\:r_{n-1}\:=\:0. r1=r2=⋯=rn−1=0.
游戏结束的时候,如果“玩家”赢了,奖励是 r n = + 1 r_n=+1 rn=+1,那么所有的回报都是 +1: 1
u
1
=
u
2
=
⋯
=
u
n
=
+
1.
u_{1}\:=\:u_{2}\:=\:\cdots\:=\:u_{n}\:=\:+1.
u1=u2=⋯=un=+1.
如果“玩家”输了,奖励是
r
n
=
−
1
r_n=-1
rn=−1, 那么所有的回报都是 -1:
u 1 = u 2 = ⋯ = u n = − 1. u_{1}\:=\:u_{2}\:=\:\cdots\:=\:u_{n}\:=\:-1. u1=u2=⋯=un=−1.
所有 n n n 步都用同样的回报,这相当于不区分哪一步棋走得好,哪一步走得烂;只要赢了, 每一步都被视为“好棋”, 假如输了,每一步都被看成“臭棋”。

回顾策略梯度:策略梯度是状态价值函数V关于 θ \theta θ的导数

两个策略网络玩游戏到终局,得到每个时刻的回报return,然后用近似策略梯度更新策略网络。
这里只更新策略网络player的参数,无需更新策略网络opponent的参数。

策略网络的方法还不够好,需要用到后面的蒙特卡洛树搜索。

为了介绍蒙特卡洛树搜索,先介绍价值网络。
Train the Value Network
这里的价值网络是对状态价值函数V的近似,不是Q的近似
用神经网络近似状态价值函数,用来评估当前形势的好坏,胜算有多大。

AlphaGo Zero中让策略网络 π \pi π和价值网络 v v v共享前面的卷积层。
策略网络的输出是361个概率值,每个值代表一个动作。策略网络的输出说明下一步该如何走动。
价值网络的输出是1个标量,是对当前状态s的打分,反映出当前状态的胜算有多大。
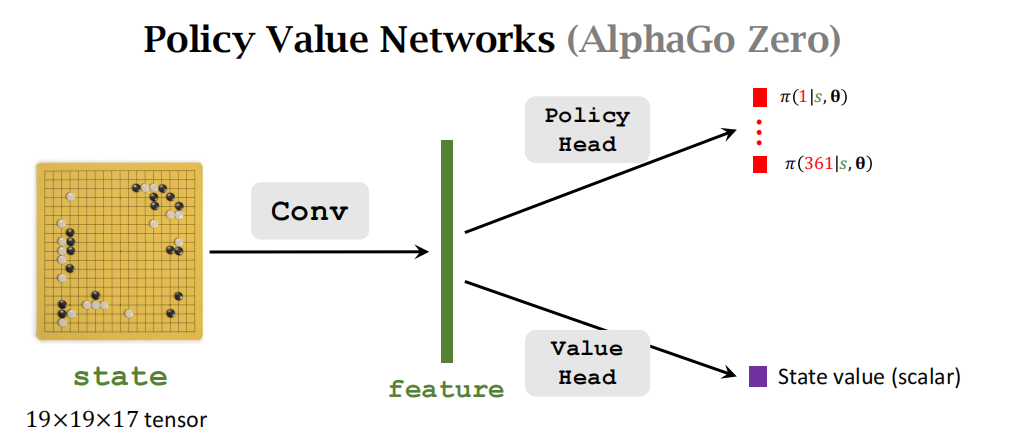
策略网络和价值网络是分别训练的,不是同时训练的。首先训练策略网络 π \pi π,然后训练价值网络 v v v。后者需要前者的帮助。这不算actor-critic方法,因为ac方法是同时训练策略网络和价值网络。
价值网络是这样训练的:让两个策略网络博弈,每下完一局,更新一次价值网络。价值网络的学习是一个回归问题,让预测值v和观测值 u t u_t ut尽可能接近,用随机梯度下降更新价值网络的参数。

Monte Carlo Tree Search(MCST)
之前训练策略网络和价值网络的目的是帮助蒙特卡洛树搜索
回忆一下高手下围棋,需要向前看好多步,看看各种可能的结果,然后做决策。

搜索未来可能发生的状态,从中选出一个胜算最大的。
蒙特卡洛树搜索的主要思想:选择一个动作a(按照动作的好坏程度选择,基于策略函数排除不好的动作),然后让策略网络自我博弈一直到游戏结束,看是否胜利,然后根据胜负和价值函数两个因素来给动作a打分。重复上述过程很多次,所以每个动作都有很多分数,选择一个分数最高的动作。
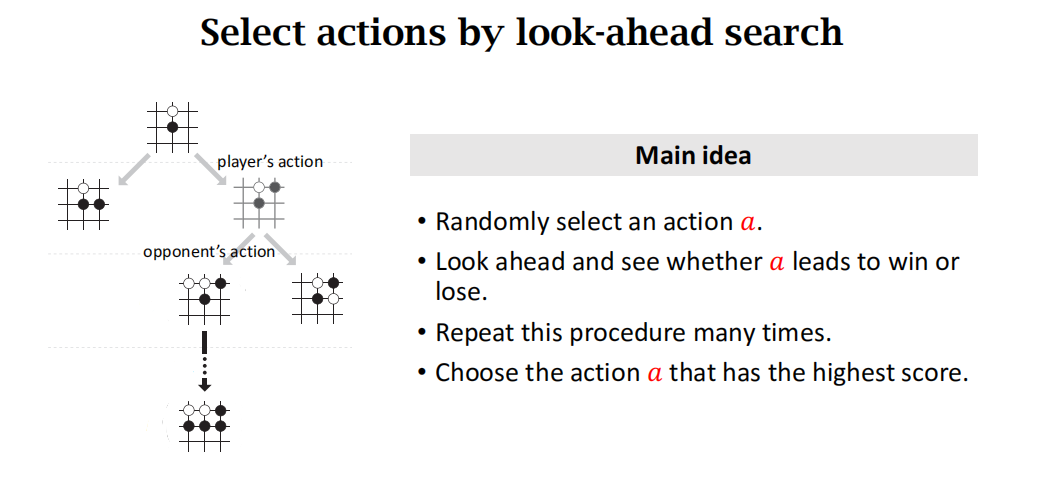
蒙特卡洛树搜索有如下4步:selection,expansion,evaluation,backup
AlphaGo每下一个棋子,都要把这四步重复很多次。
selection:player执行动作a,这是假想动作,不会实际执行。
expansion:opponent也执行一个动作,此时状态更新。这里也是假想动作。使用策略网络作为假想对手,不是真正的实际的对手。
evaluation:给上述选择的动作a打分,分数有两部分构成:一是价值网络的打分v,另一个是游戏的结果(策略网络自我博弈到游戏结束)获得奖励r。两者的平均值作为分数。
backup:反向传播,用上述打分来更新动作的分数。

MCTS的每一次模拟选出一个动作a,执行这个动作,然后把一局游戏进行到底,用胜负来评价这个动作的好坏。MCTS的每一次模拟分为四个步骤:选择(selection)、扩 展(expansion)、求值(evaluation)、回溯(backup)。
第一步——选择(Selection)
观测棋盘上当前的格局,找出所有空位,然后判断其中哪些位置符合围棋规则;每个符合规则的位置对应一个可行的动作。每一步至少有几十、甚至上百个可行的动作;假如挨个搜索和评估所有可行动作,计算量会大到无法承受。虽然有几十、上百个可行动作,好在只有少数几个动作有较高的胜算。第一步—— 选择——的目的就是找出胜算较高的动作,只搜索这些好的动作,忽略掉其他的动作。
如何判断动作a的好坏呢?有两个指标:第一,动作a的胜率;第二,策略网络给动作a的评分(概率值)。用下面这个分值评价a的好坏:
s c o r e ( a ) ≜ Q ( a ) + η 1 + N ( a ) ⋅ π ( a ∣ s ; θ ) . ( 18.1 ) \mathrm{score}(a)\quad\triangleq\quad Q(a)+\frac{\eta}{1+N(a)}\cdot\pi(a|s;\boldsymbol{\theta}). \quad{(18.1)} score(a)≜Q(a)+1+N(a)η⋅π(a∣s;θ).(18.1)
此处的 η \eta η 是个需要调的超参数。公式中 N ( a ) N(a) N(a)、 Q ( a ) Q(a) Q(a) 的定义如下:
- N ( a ) N(a) N(a) 是动作 a a a 已经被访问过的次数。初始的时候,对于所有的 a a a,令 N ( a ) ← 0 N(a)\gets0 N(a)←0。动作 a a a 每被选中一次,我们就把 N ( a ) N(a) N(a) 加一: N ( a ) ← N ( a ) + 1 N(a)\gets N(a)+1 N(a)←N(a)+1。
- Q ( a ) Q(a) Q(a) 是之前 N ( a ) N(a) N(a) 次模拟算出来的动作价值,主要由胜率和价值函数决定。 Q ( a ) Q(a) Q(a) 的初始值是 0; 动作 a a a 每被选中一次,就会更新一次 Q ( a ) Q(a) Q(a); 后面会详解。
可以这样理解公式 (18.1):
- 如果动作 a a a 还没被选中过,那么 Q ( a ) Q(a) Q(a) 和 N ( a ) N(a) N(a) 都等于零,因此可得
score ( a ) ∝ π ( a ∣ s ; θ ) , \operatorname{score}(a)\quad\propto\quad\pi(a|s;\boldsymbol{\theta}), score(a)∝π(a∣s;θ),
也就是说完全由策略网络评价动作 a a a 的好坏。
- 如果动作 a a a 已经被选中过很多次,那么 N ( a ) N(a) N(a) 就很大,导致策略网络在 score ( a ) (a) (a) 中的权重降低。当 N ( a ) N(a) N(a) 很大的时候,有
score ( a ) ≈ Q ( a ) , \begin{matrix}\text{score}(a)&\approx&Q(a),\end{matrix} score(a)≈Q(a),
此时主要基于 Q ( a ) Q(a) Q(a) 判断 a a a 的好坏,而策略网络已经无关紧要。
- 系数 1 1 + N ( a ) \frac1{1+N(a)} 1+N(a)1 的另一个作用是鼓励探索,也就是让被选中次数少的动作有更多的机会被选中。假如两个动作有相近的 Q Q Q 分数和 π 分数,那么被选中次数少的动作的score 会更高。
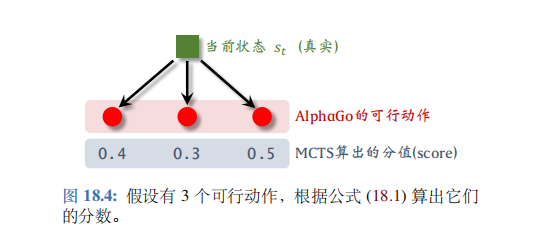
MCTS 根据公式 (18.1) 算出所有动作的分数 score ( a ) , ∀ a (a),\:\forall a (a),∀a。MCTS 选择分数最高的动作。图18.4 的例子中有3 个可行动作,分数分别为0.4、0.3、0.5。第三个动作分数最高,会被选中,这一轮模拟会执行这个动作。(只是在模拟中执行而已,不是 AlphaGo 真的走一步棋)。

第二步——扩展 (Expansion)
把第一步选中的动作记作 a t a_t at, 它只是个假想的动作,只在“模拟器”中执行,而不是 AlphaGo 真正执行的动作。
AlphaGo 需要考虑这样一个问题:假如它执行动作
a
t
a_t
at,那么对手会执行什么动作呢?对手肯定不会把自己的想法告诉 AlphaGo, 那么 AlphaGo 只能自己猜测对手的动作。AlphaGo 可以“推已及人”: 如果 AlphaGo 认为几个动作很好,对手也会这么认为。所以 AlphaGo 用策略网络模拟对手, 根据策略网络随机抽样一个动作:
a
t
′
∼
π
(
⋅
∣
s
t
′
;
θ
)
.
a_{t}^{\prime}\:\sim\:\pi(\:\cdot\:|\:s_{t}^{\prime};\:\boldsymbol{\theta})\:.
at′∼π(⋅∣st′;θ).
此处的状态 s ′ s^{\prime} s′ 是站在对手的角度观测到的棋盘上的格局,动作 a t ′ a_t^{\prime} at′ 是 (假想) 对手选择的动作。
图 18.5 的例子中对手有四种可行动作,AlphaGo 用策略网络算出每个动作的概率值,然后根据概率值随机抽样一个对手的动作,记作 a t ′ a_t^{\prime} at′。
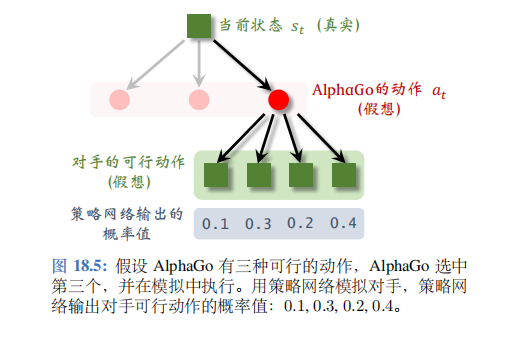
假设根据概率值 0.1,0.3,0.2, 0.4 做随机抽样,选中第二种动作;见图 18.6。从 AlphaGo 的角度来看,对手的动作就是AlphaGo 新的状态。
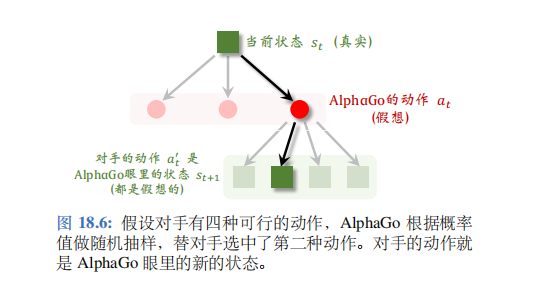
AlphaGo 需要在模拟中跟对手将一局游戏进行下去,所以需要一个模拟器(即环境)。在模拟器中,AlphaGo 每执行一个动作 a k a_k ak, 模拟器就会返回一个新的状态 s k + 1 s_{k+1} sk+1。想要搭建一个好的模拟器,关键在于使用正确的状态转移函数 p ( s k + 1 ∣ s k , a k ) ; p(s_{k+1}|s_k,a_k); p(sk+1∣sk,ak); 如果状态转移函数与事实偏离太远,那么用模拟器做 MCTS 是毫无意义的。
AlphaGo 模拟器利用了围棋游戏的对称性:AlphaGo 的策略, 在对手看来是状态转移函数;对手的策略,在 AlphaGo 看来是状态转移函数。最理想的情况下,模拟器的状态转移函数是对手的真实策略;然而 AlphaGo 并不知道对手的真实策略。AlphaGo 退而求其次,用 AlphaGo 自己训练出的策略网络 π \pi π 代替对手的策略,作为模拟器的状态转移函数。
想要用 MCTS 做决策,必须要有模拟器,而搭建模拟器的关键在于构造正确的状态转移函数 p ( s k + 1 ∣ s k , a k ) p(s_{k+1}|s_k,a_k) p(sk+1∣sk,ak)。从搭建模拟器的角度来看,围棋是非常简单的问题:由于围棋的对称性,可以用策略网络作为状态转移函数。但是对于大多数的实际问题,构造状态转移函数是非常困难的。比如机器人、无人车等应用,状态转移的构造需要物理模型,要考虑到力、运动、以及外部世界的干扰。如果物理模型不够准确,导致状态转移函数偏 离事实太远,那么 MCTS 的模拟结果就不可靠。

第三步一一求值 (Evaluation)
从状态
s
t
+
1
s_{t+1}
st+1 开始,双方都用策略网络
π
\pi
π 做决策,在模拟器中交替落子,直到分出胜负;见图 18.7。AlphaGo 基于状态
s
k
s_k
sk,根据策略网络抽样得到动作
a
k
∼
π
(
⋅
∣
s
k
;
θ
)
.
a_k\:\sim\:\pi(\:\cdot\:|\:s_k;\:\boldsymbol{\theta}).
ak∼π(⋅∣sk;θ).
对手基于状态 s k ′ s_k^{\prime} sk′(从对手角度观测到的棋盘上的格局), 根据策略网络抽样得到动作
a k ′ ∼ π ( ⋅ ∣ s k ′ ; θ ) . a_k'\sim\pi(\cdot|s_k';\theta). ak′∼π(⋅∣sk′;θ).
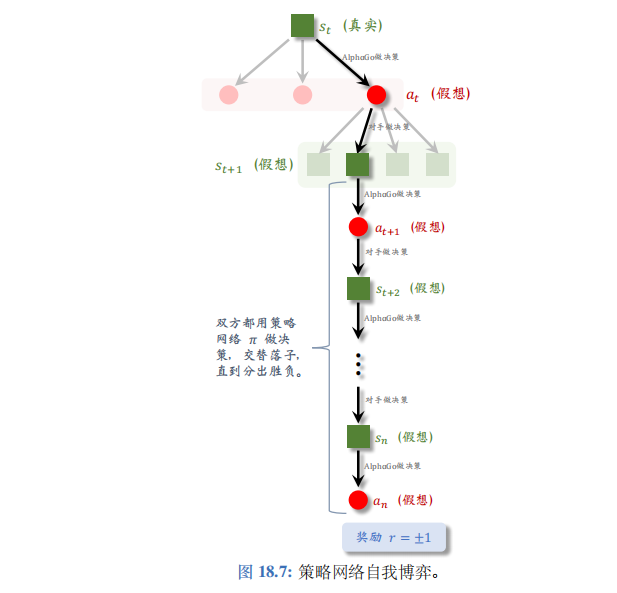
当这局游戏结束时,可以观测到奖励。如果 AlphaGo 胜利,则 r = + 1 r=+1 r=+1,否则 r = − 1 r=-1 r=−1。
回顾一下,棋盘上真实的状态是 s t s_t st, AlphaGo 在模拟器中执行动作 a t a_t at,然后模拟器中的对手执行动作 a t ′ a_t^{\prime} at′,带来新的状态 s t + 1 s_{t+1} st+1。状态 s t + 1 s_{t+1} st+1 越好,则这局游戏胜算越大。
- 如果 AlphaGo 赢得这局模拟 ( r = + 1 ) (r=+1) (r=+1),则说明 s t + 1 s_{t+1} st+1 可能很好;如果输了 ( r = − 1 ) (r=-1) (r=−1),以反映出 s t + 1 s_{t+1} st+1 的好坏。
- 此外,还可以用价值网络 v v v 评价状态 s t + 1 s_{t+1} st+1的好坏。价值 v ( s t + 1 ; w ) v(s_{t+1};w) v(st+1;w) 越大,则说明状态 s t + 1 s_{t+1} st+1越好。
奖励 r 是模拟获得的胜负,是对 s t + 1 s_{t+1} st+1 很可靠的评价,但是随机性太大。价值网络的评估 v ( s t + 1 ; w ) v(s_{t+1};\boldsymbol{w}) v(st+1;w) 没有 r r r 可靠,但是价值网络更稳定、 随机性小。AlphaGo 的解决方案是把奖励 r r r 与价值网络的输出 v ( s t + 1 ; w ) v(s_{t+1};w) v(st+1;w) 取平均,记作:
V ( s t + 1 ) ≜ r + v ( s t + 1 ; w ) 2 , V(s_{t+1})\:\triangleq\:\frac{r\:+\:v(s_{t+1};\boldsymbol{w})}{2}, V(st+1)≜2r+v(st+1;w),
把它记录下来,作为对状态 s t + 1 s_{t+1} st+1 的评价。
实际实现的时候,AlphaGo 还训练了一个更小的神经网络,它做决策更快。MCTS 在第一步和第二步用大的策略网络,第三步用小的策略网络。读者可能好奇,为什么在且仅在第三步用小的策略网络呢?第三步两个策略网络交替落子,通常要走一两百步, 导致第三步成为 MCTS 的瓶颈。用小的策略网络代替大的策略网络,可以大幅加速 MCTS。
自己和对方交替做决策下棋的过程称为fast rollout。
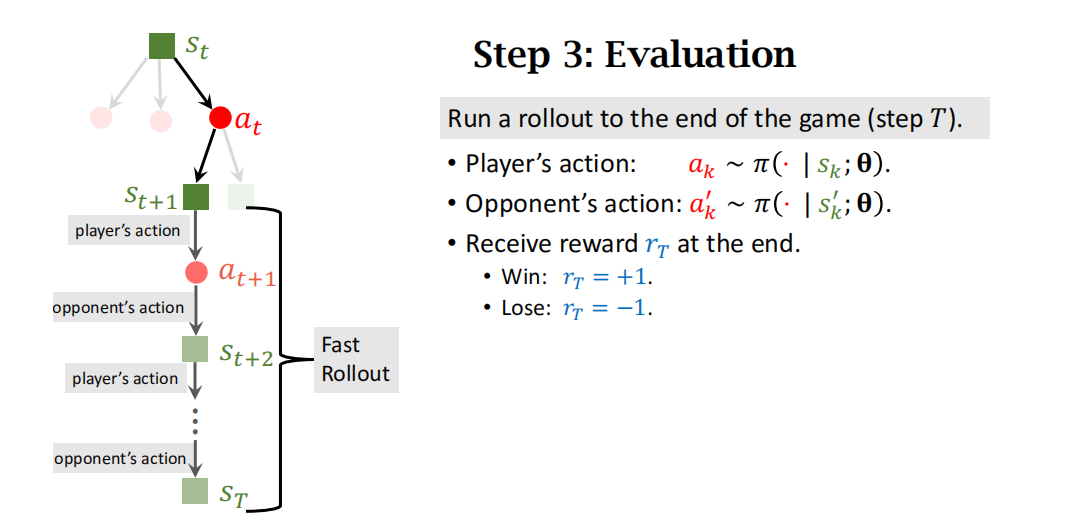
除了用奖励r来评价状态 s t + 1 s_{t+1} st+1,AlphaGo还用价值网络v来评价状态 s t + 1 s_{t+1} st+1
两者取平均,作为 s t + 1 s_{t+1} st+1的分数。

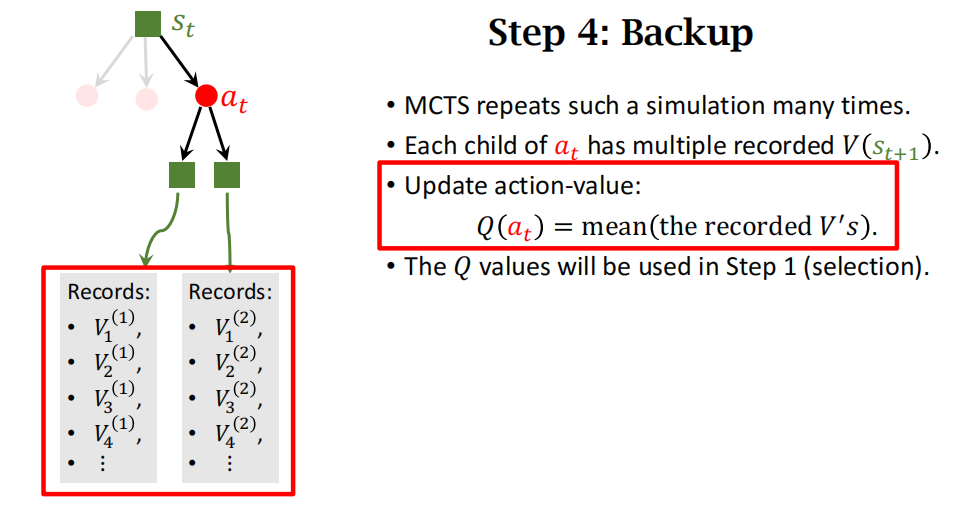
第四步一一回溯 (Backup)
第三步一一求值——算出了第 t + 1 t+1 t+1步某一个状态的价值,记作 V ( s t + 1 ) V(s_{t+1}) V(st+1); 每一次模拟都会得出这样一个价值,并且记录下来。模拟会重复很多次,于是第 t + 1 t+1 t+1 步每一种状态下面可以有多条记录;如图 18.8 所示。第 t t t 步的动作 a t a_t at 下面有多个可能的状态(子节点),每个状态下面有若干条记录。把 a t a_t at 下面所有的记录取平均,记作价值 Q ( a t ) Q(a_t) Q(at),它可以反映出动作 a t a_t at 的好坏。
在图 18.8 中, a t a_t at 下面一共有 12 条记录, Q ( a t ) Q(a_t) Q(at) 是 12 条记录的均值。
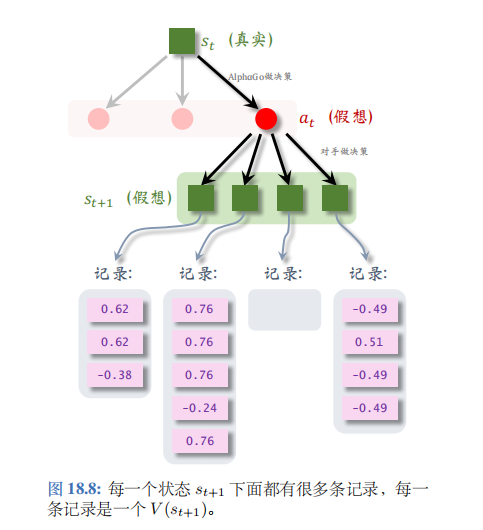
给定棋盘上的真实状态 s t s_t st,有多个动作 a a a 可供选择。对于所有的 a a a,价值 Q ( a ) Q(a) Q(a) 的初始值是零。动作 a a a 每被选中一次 (成为 a t a_t at),它下面就会多一条记录,我们就对 Q ( a ) Q(a) Q(a) 做一次更新。
回顾第一步——选择 (Selection): 基于棋盘上真实的状态 s t s_t st, MCTS 需要从可行的动作中选出一个,作为 a t a_t at。MCTS 计算每一个动作 a a a 的分数:
s c o r e ( a ) ≜ Q ( a ) + η 1 + N ( a ) ⋅ π ( a ∣ s ; θ ) , ∀ a , \mathrm{score}(a)\quad\triangleq\quad Q(a)\:+\:\frac{\eta}{1+N(a)}\:\cdot\:\pi(a|s;\boldsymbol{\theta}),\quad\forall\:a, score(a)≜Q(a)+1+N(a)η⋅π(a∣s;θ),∀a,
然后选择分数最高的 a a a。MCTS 算出的 Q ( a ) Q(a) Q(a) 的用途就是这里。
第四步:
MCTS会重复上述模拟很多次,所以每个状态下都有很多条记录,每个动作 a t a_t at下面有很多子节点,所以 a t a_t at对应很多记录,将 a t a_t at下面的所有记录做平均作为 a t a_t at新的价值 Q ( a t ) Q(a_t) Q(at)。
Decision Making after MCTS
MCTS 的决策
上面讲解了单次模拟的四个步骤,注意,这只是单次模拟而已。MCTS 想要真正做出一个决策 (即往真正的棋盘上落一个棋子), 需要做成千上万次模拟。在做了无数次模拟之后,MCTS 做出真正的决策:
a
t
=
argmax
a
N
(
a
)
.
a_{t}\:=\:\operatorname*{argmax}_{a}\:N(a).
at=aargmaxN(a).
此时 AlphaGo 才会真正往棋盘上放一个棋子。
为什么要依据 N ( a ) N(a) N(a) 来做决策呢?在每一次模拟中,MCTS 找出所有可行的动作 { a } \{a\} {a} 计算它们的分数 score$( a) $,然后选择其中分数最高的动作,然后在模拟器里执行。如果某个动作 a a a 在模拟中胜率很大,那么它的价值 Q ( a ) Q(a) Q(a) 就会很大,它的分数 score$( a) $ 会很高: 于是它被选中的几率就大。也就是说如果某个动作 a a a 很好,它被选中的次数 N ( a ) N(a) N(a) 就会大。
观测到棋盘上当前状态 s t s_t st, MCTS 做成千上万次模拟,记录每个动作 a a a 被选中的次数 N ( a ) N(a) N(a),最终做出决策 a t = argmax a N ( a ) a_t=\operatorname{argmax}_aN(a) at=argmaxaN(a)。到了下一时刻,状态变成了 s t + 1 s_{t+1} st+1, MCTS 把所有动作 a a a 的 Q ( a ) Q(a) Q(a)、 N ( a ) N(a) N(a) 全都初始化为零,然后从头开始做模拟,而不能利用上一次的结果。
AlphaGo 下棋非常“暴力” 每走一步棋之前,它先在“脑海里”模拟几千、几万局、它可以预知它每一种动作带来的后果,对手最有可能做出的反应都在 AlphaGo 的算计之内。由于计算量差距悬殊,人类面对 AlphaGo 时不太可能有胜算。这样的比赛对人来说是不公平的;假如李世石下每一颗棋子之前,先跟柯洁模拟一千局,或许李世石的胜算会大于 AlphaGo。

MCTS: Summary
MCTS 4步:
第一,selection,根据动作的分数,选出分数最高的动作。
第二,expansion,用策略网络来模拟对手的动作,产生新的状态。
第三,evaluation,通过自我博弈和价值网络这两个途径算出两个分数,记录它们的平均值。
第四,backup,用第三步算出来的分数来更新这个动作的分数。
AlphaGo每走一步,都要进行成千上万次模拟。每次模拟都要重复以上四步。

Summary
AlphaGo的训练分三步:
第一步:用behavior cloning初步训练一个策略网络,这一步训练用的是16万局游戏的棋谱,让策略网络来模仿人类玩家的动作。这一步之后策略网络可以打败业余玩家。
第二步:用策略梯度进一步训练策略网络,AlphaGo让策略网络做自我博弈,用游戏胜负这个信息来更新策略网络,经过这个步骤,策略网络的能力变得更强。
第三步:训练一个价值网络,用来评估状态的好坏。这一步让策略网络做自我博弈,用胜负结果作为target,让价值网络来拟合这个target。训练价值网络,实际上就是做回归(regression)。
虽然可以用策略网络来下棋,但是更好的办法是用蒙特卡洛树搜索。AlphaGo每走一步都要做成千上万次搜索,计算每一个动作的胜算有多大,给每个动作打分,最终AlphaGo会执行分数最高的动作。

AlphaGo Zero
AlphaGo Zero完胜AlphaGo,它俩的区别有两个:
-
AlphaGo Zero没有做behavior cloning。
-
AlphaGo Zero在训练策略网络的时候就用了蒙特卡洛树搜索,让策略网络来模仿搜索做出来的动作。
AlphaGo是模仿人类玩家,AlphaGo Zero是模仿蒙特卡洛树搜索。

在围棋游戏中,人类经验(behavior cloning)是有害的(或者说性能有限)。
但是behavior cloning还是有用的尤其是物理世界的实体,比如手术机器人、无人驾驶汽车。先学习人类经验再做强化学习。

AlphaGo Zero是如何训练策略网络的:使用MCTS。

后记
截至2024年1月28日16点32分,完成第五个视频的学习。学习了AlphaGo和更强的AlphaGo Zero的原理,主要是蒙特卡洛树搜索MCST。