目录
0-1背包理论基础
0-1背包问题
二维dp数组01背包
算法实现
一维dp数组01背包
编辑算法实现
416. 分割等和子集
前言
思路
算法实现
总结
0-1背包理论基础
0-1背包问题
题目链接
https://kamacoder.com/problempage.php?pid=1046 有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。
这是一道标准的背包问题，如果利用暴力求解，每一件物品其实只有两个状态，取或者不取，所以可以使用回溯法搜索出所有的情况，那么时间复杂度就是$o(2^n)$，这里的n表示物品数量。
所以暴力的解法是指数级别的时间复杂度。进而才需要动态规划的解法来进行优化！
举一个例子：背包最大重量为4。
物品为：
| 重量 | 价值 | |
|---|---|---|
| 物品0 | 1 | 15 |
| 物品1 | 3 | 20 |
| 物品2 | 4 | 30 |
问背包能背的物品最大价值是多少？
二维dp数组01背包
依然使用动态规划五部曲进行分析：
1.确定dp数组以及下标的含义：
对于背包问题，有一种写法， 是使用二维数组，dp[i][j] 表示从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少。仅看二维数组不太容易理解，结合表格图来进行分析下比较容易理解。
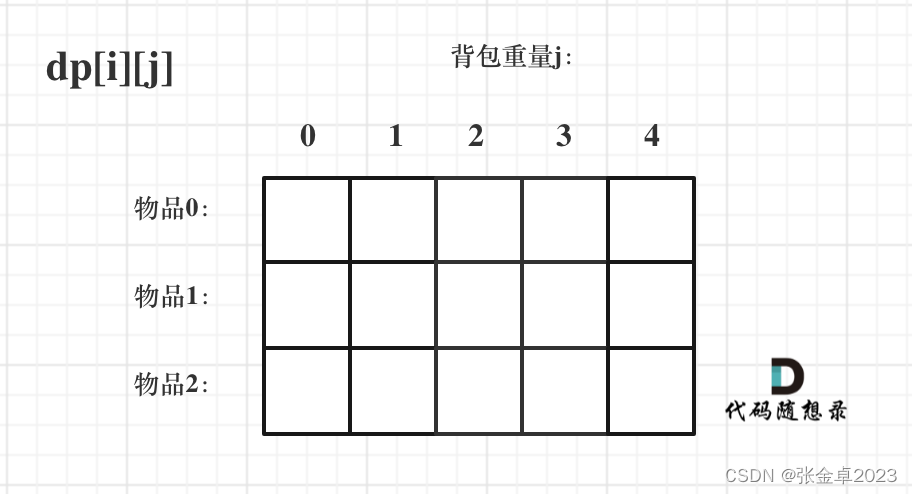
2.确定递推公式：
有两个方向可以推出dp[i][j]：
- 不放物品i：由dp[i - 1][j]推出里面不放物品i的最大价值，此时dp[i][j]就是dp[i - 1][j]。(其实就是当物品i的重量大于背包j的重量时，物品i无法放进背包中，所以背包内的价值依然和前面相同。)；
- 放物品i：dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值，那么dp[i - 1][j - weight[i]] + value[i] （物品i的价值），就是背包放物品i得到的最大价值 。
所以递归公式： dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])；
3.初始化dp数组
关于初始化，一定要和dp数组的定义吻合，否则到递推公式的时候就会越来越乱。
如果背包容量j为0的话，即dp[i][0]，无论是选取哪些物品，背包价值总和一定为0。如图：
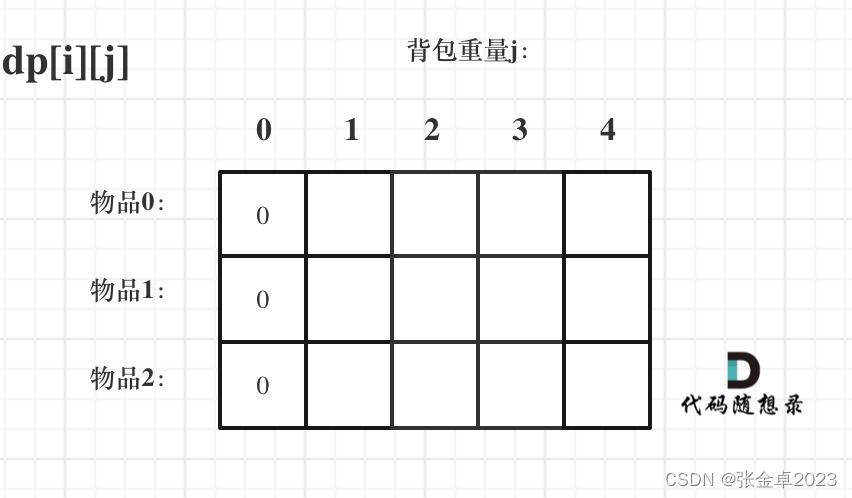
状态转移方程 dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 可以看出i 是由 i-1 推导出来，那么i为0的时候就一定要初始化。dp[0][j]，即：i为0，存放编号0的物品的时候，各个容量的背包所能存放的最大价值。那么很明显当 j < weight[0]的时候，dp[0][j] 应该是 0，因为背包容量比编号0的物品重量还小。当j >= weight[0]时，dp[0][j] 应该是value[0]，因为背包容量放足够放编号0物品。
此时dp数组初始化情况如图所示：
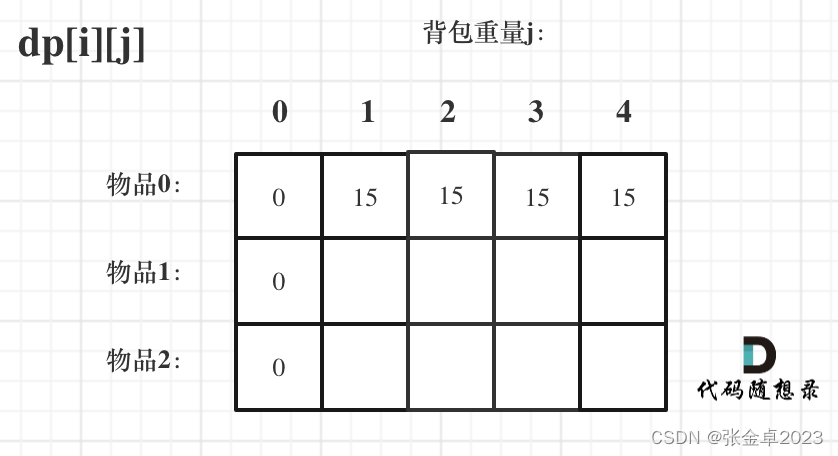
dp[0][j] 和 dp[i][0] 都已经初始化了，那么其他下标应该初始化多少呢？
其实从递归公式： dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 可以看出dp[i][j] 是由左上方数值推导出来了，那么 其他下标初始为什么数值都可以，因为都会被覆盖。因此初始化为任何值都可以，但只不过一开始就统一把dp数组统一初始为0，更方便一些，如图：
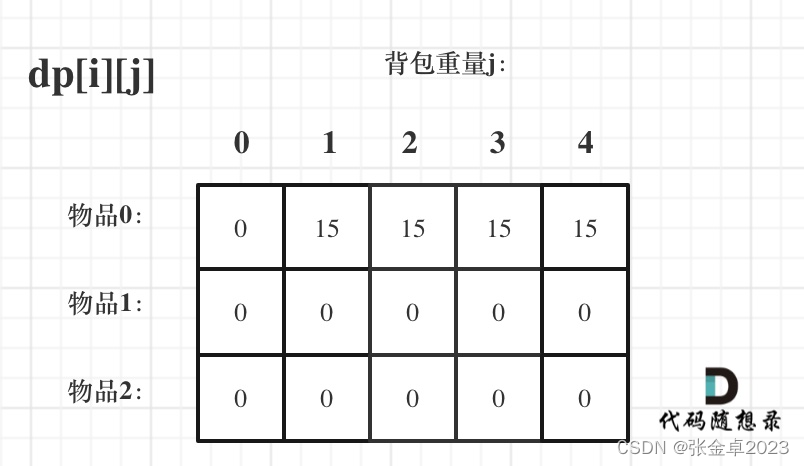
4.确定遍历顺序：
有两个遍历的维度：物品与背包重量。先遍历物品还是先遍历背包其实都可以，但是先遍历物品更好理解，并且可以和一维dp数组01背包问题的实现保持一致。
其实背包问题里，两个for循环的先后循序是非常有讲究的，理解遍历顺序其实比理解推导公式难多了。
5.举例推导dp数组
来看一下对应的dp数组的数值，如图：
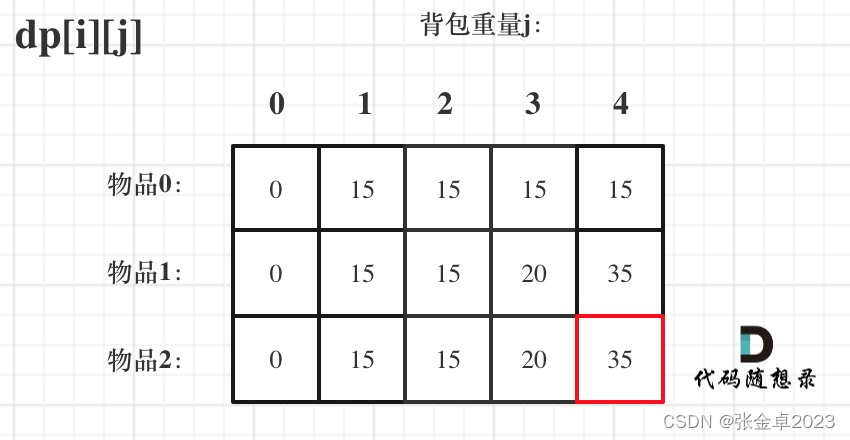
算法实现
#include <bits/stdc++.h>
using namespace std;
int n, bagweight;
void solve(){
vector<int> weight(n, 0);
vector<int> value(n, 0);
for (int i = 0; i < n; i++){
cin >> weight[i];
}
for (int j = 0; j < n; j++){
cin >> value[j];
}
// 创建dp数组并部分初始化
vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));
// 初始化dp数组
for (int j = weight[0]; j <= bagweight; j++){
dp[0][j] = value[0];
}
for (int i = 1; i < weight.size(); i++){
for (int j = 0; j <= bagweight; j++){
if (j < weight[i]) dp[i][j] = dp[i - 1][j];
else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
}
cout << dp[weight.size() - 1][bagweight] << endl;
}
int main(){
while (cin >> n >> bagweight) {
solve();
}
return 0;
}一维dp数组01背包
对于背包问题其实状态都是可以压缩的。
在使用二维数组的时候，递推公式：dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
其实可以发现如果把dp[i - 1]那一层拷贝到dp[i]上，并且只用一个一维数组表示，只用dp[j]（一维数组，也可以理解是一个滚动数组）。
这就是滚动数组的由来，需要满足的条件是上一层可以重复利用，直接拷贝到当前层。
利用动态规划五部曲来进行分析：
1.确定dp数组及其下标的含义：
在一维dp数组中，dp[j]表示：容量为j的背包，所背的物品价值可以最大为dp[j]。
2.一维dp数组递推公式：
dp[j]可以通过dp[j - weight[i]]推导出来，dp[j - weight[i]]表示容量为j - weight[i]的背包所背的最大价值。dp[j - weight[i]] + value[i] 表示 容量为 j - 物品i重量 的背包 加上 物品i的价值。（也就是容量为j的背包，放入物品i了之后的价值即：dp[j]）。
此时dp[j]有两个选择，一个是取自己dp[j] 相当于 二维dp数组中的dp[i-1][j]，即不放物品i，一个是取dp[j - weight[i]] + value[i]，即放物品i，指定是取最大的，毕竟是求最大价值。
所以递推公式为：dp[j] = max(dp[j], dp[j - weight[i]] + value[i])。可以看出相对于二维dp数组的写法，就是把dp[i][j]中i的维度去掉了。
3.一维dp数组初始化：
dp[j]表示：容量为j的背包，所背的物品价值可以最大为dp[j]，那么dp[0]就应该是0，因为背包容量为0所背的物品的最大价值就是0。dp数组在推导的时候一定是取价值最大的数，如果题目给的价值都是正整数那么非0下标都初始化为0就可以了。
这样才能让dp数组在递归公式的过程中取的最大的价值，而不是被初始值覆盖了。
那么我假设物品价值都是大于0的，所以dp数组初始化的时候，都初始为0就可以了。
4.一维dp数组遍历顺序：
for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}二维dp遍历的时候，背包容量是从小到大，而一维dp遍历的时候，背包是从大到小。因为倒序遍历是为了保证物品i只被放入一次！。但如果一旦正序遍历了，那么物品0就会被重复加入多次！因为当前层拷贝的是上一层的值，前面的数值不能先被更改。
为什么二维dp数组遍历的时候不用倒序呢？
因为对于二维dp，dp[i][j]都是通过上一层即dp[i - 1][j]计算而来，本层的dp[i][j]并不会被覆盖！
还要注意for循环的遍历顺序，一维dp的写法，背包容量一定是要倒序遍历，如果遍历背包容量放在上一层，那么每个dp[j]就只会放入一个物品，即：背包里只放入了一个物品。
5.举例推导dp数组：
一维dp，分别用物品0，物品1，物品2 来遍历背包，最终得到结果如下：
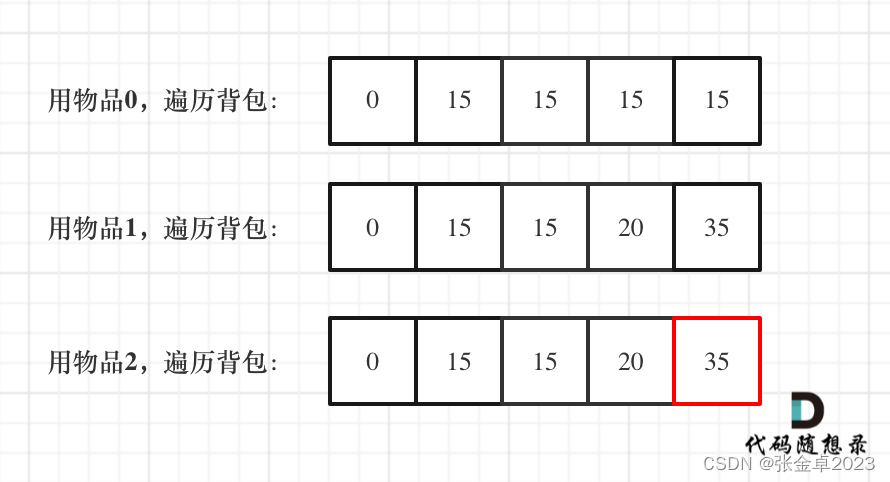算法实现
include <bits/stdc++.h>
using namespace std;
int n, bagweight;
void solve(){
vector<int> weight(n, 0);
vector<int> value(n, 0);
for (int i = 0; i < n; i++) {
cin >> weight[i];
}
for (int j = 0; j < n; j++) {
cin >> value[j];
}
vector<int> dp(bagweight + 1, 0);
for (int i = 0; i < weight.size(); i++){
for (int j = bagweight; j >= weight[i]; j--){
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
cout << dp[bagweight] << endl;
}
int main(){
while (cin >> n >> bagweight) {
solve();
}
return 0;
}416. 分割等和子集
题目链接
文章链接
前言
这道题目是要找是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。那么只要找到集合里能够出现 sum / 2 的子集总和，就算是可以分割成两个相同元素和子集了。本题的难点主要在于如何将题目条件转换为我们知道的01背包条件。
思路
背包问题有多种背包方式，常见的有：01背包、完全背包、多重背包、分组背包和混合背包等等。
要注意题目描述中商品是不是可以重复放入。即一个商品如果可以重复多次放入是完全背包，而只能放入一次是01背包。
首先，本题要求集合里能否出现总和为 sum / 2 的子集。只有确定了如下四点，才能把01背包问题套到本题上来。
- 背包的体积为sum / 2
- 背包要放入的商品（集合里的元素）重量为 元素的数值，价值也为元素的数值
- 背包如果正好装满，说明找到了总和为 sum / 2 的子集。
- 背包中每一个元素是不可重复放入。
以上分析完，我们就可以套用01背包，来解决这个问题了。还是使用动态规划五部曲来进行。
1.确定dp数组及下标含义
dp[j] 表示： 容量为j的背包，所背的物品价值最大可以为dp[j]。而本题中每一个元素的数值既是重量，也是价值。dp[j]表示 背包总容量（所能装的总重量）是j，放进物品后，背的最大重量为dp[j]。
那么如果背包容量为target， dp[target]就是装满 背包之后的重量，所以 当 dp[target] == target 的时候，背包就装满了。
2.确定递推公式：
一维01背包的递推公式为：dp[j] = max(dp[j], dp[j - weight[i]] + value[i])；本题，相当于背包里放入数值，那么物品i的重量是nums[i]，其价值也是nums[i]。
所以递推公式：dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
3.dp数组的初始化：
从dp[j]的定义来看，首先dp[0]一定是0。其他数值要尽量小，尽量在后面的比价中不要覆盖掉要替换的值，为了方便可以都初始化为0。
4.确定遍历顺序：
在上面的理论基础中讲到过如果使用一维dp数组，物品遍历的for循环放在外层，遍历背包的for循环放在内层，且内层for循环倒序遍历！
5.举例推导dp数组：
dp[j]的数值一定是小于等于j的。如果dp[j] == j 说明，集合中的子集总和正好可以凑成总和j，理解这一点很重要。以例1为例：
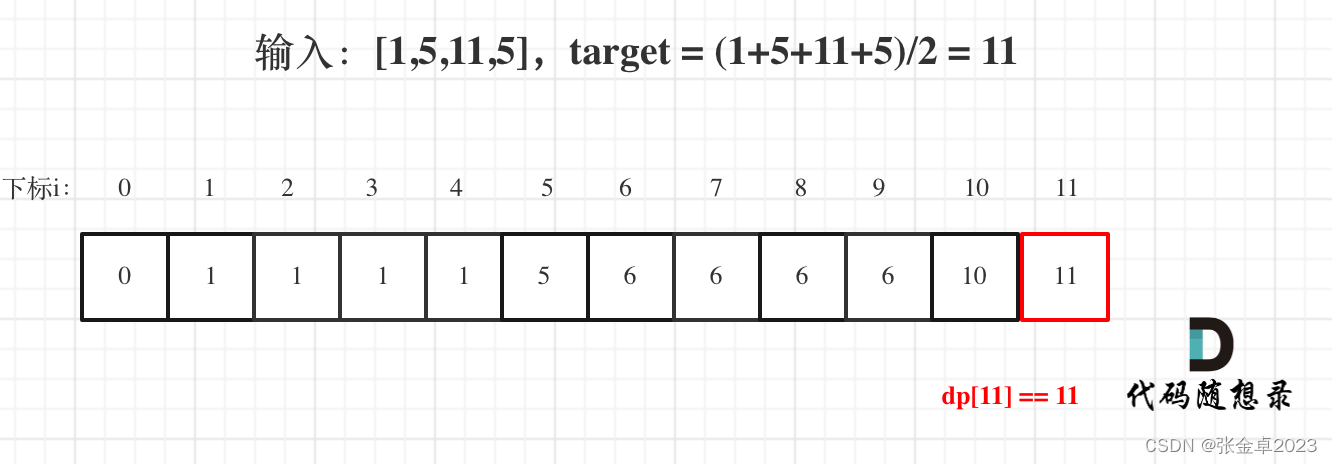
最后dp[11] == 11，说明可以将这个数组分割成两个子集，使得两个子集的元素和相等。
算法实现
class Solution {
public:
bool canPartition(vector<int>& nums) {
vector<int> dp(10001, 0);
// int sum = 0;
// for (int i = 0; i < nums.size(); i++) {
// sum += nums[i];
// }
int sum = accumulate(nums.begin(), nums.end(),0);
if (sum % 2 == 1) return false;
int target = sum / 2;
for (int i = 0; i < nums.size(); i++) { // 遍历物品
for (int j = target; j >= nums[i]; j--){ // 遍历背包
dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
}
}
if (dp[target] == target) return true;
return false;
}
};总结
今天了解了背包问题中的0-1背包问题，对于二维dp数组和一维dp数组的原理和实现有了一定了解，并对其进行了简单的初步应用。
