文章目录
- 前言
- 方差分析
- 方差分析的原理
- 什么是方差分析
- 误差分解
- 单因子方差分析
- 数学模型
- 效应检验
- 练习
前言
本片开始介绍有关方差分析的知识。
方差分析
方差分析的基本原理是在20世纪20年代由英国统计学家Ronald A.Fisher在进行实验设计时为解释实验数据而首先引入的。方差分析是一种统计方法。目前,方差分析方法广泛应用于分析心理学、生物学、工程和医药的实验数据。本章首先介绍方差分析的基本原理,然后介绍只涉及一个因变量的单因子独立样本和双因子独立样本的方差分析方法
方差分析的原理
什么是方差分析
方差分析(analysis of variance,ANOVA) 是分析类别自变量对数值因变量影响的一种统计方法 。自变量对因变量的影响也称为自变量效应(effect)。由于影响效应的大小表现在因变量的误差里有多少是由自变量造成的,因此,方差分析是通过对数据误差的分析来检验这种效应是否显著。
研究分类型自变量对数值型因变量的影响
一个或多个分类型自变量
两个或多个 (k 个) 处理水平或分类
一个数值型因变量
有单因子方差分析和双因子方差分析
单因子方差分析:涉及一个分类的自变量
双因子方差分析:涉及两个分类的自变量
例题:
(数据:example8_1.RData)为分析小麦品种对产量的影响,一家研究机构挑选了3个小麦品种:品种1、品种2、品种3,然后选择条件和面积相同的30个地块,每个品种在10个地块上试种,实验获得的产量数据如下表所示。

分析“小麦品种” 对“产量”的影响
在上表中,“小麦品种”是类别变量,称为实验的因子(factor),品种1、品种2、品种3是因子的3个不同取值,称为处理(treatment)或水平(level)
这里的“地块”就是接受处理的对象或实体,称为实验单元(experiment unit)
产量则是因变量,每个地块上获得的产量是样本观察值。分析小麦品种对产量影响的统计方法就是方差分析。
如果只分析品种一个因子对产量的影响,则称为单因子方差分析(one-way analysis of variance)
如果两个因子对产量的单独影响,但不考虑它们对产量的交互效应(interaction),则称为只考虑主效应(main effect)的双因子方差分析,或称为无重复双因子分析(two-factor without replication)
如果除了考虑两个因子对产量的单独影响外,还考虑二者对产量的交互效应,则称为考虑交互效应的双因子方差分析,或称为可重复双因子分析(two-factor with replication)
误差分解
怎样分析小麦品种对产量是否有显著影响呢?由于品种对产量的影响效应体现在产量数值的误差里,因此,分析时首先应从数据误差的分析入手。方差分析的原理就是通过对数据误差的分析来判断类别自变量(小麦品种)对数值因变量(产量)的影响效应是否显著。
怎样分析数据的误差呢?从上表可以看出,每个品种(每种处理)各有10个实验数据,这些数据实际上是从每个品种的产量总体中抽出来的样本量为10的随机样本,共获得3个样本的30个实验数据.可以看出,这30个产量数据是不同的。
因此有如下定义
总误差(total error)
反映全部观测数据的误差
所抽取的全部30个地块的产量之间的误差
总误差可能是由于不同处理(小麦的不同品种)造成的,也可能是由于其他随机因素造成的。
处理误差(treatment error)—组间误差(between-group error)(处理误差来自不同的处理之间)
由于不同处理造成的误差,它反映了处理(品种)对观测数据(产量)的影响,因此称为处理效应(treatment effect)
随机误差(random error)—组内误差(within-group error)
由于随机因子造成的误差,也简称为误差(error)
由其他随机因素对观测数据造成的误差称为随机误差(random error),也简称为误差(error)。本例中,随机误差反映了除品种外其他随机因素对产量的影响。
由于随机误差主要存在于每种处理的内部,因此,有时也称为组内误差(within-group error)。
随机误差(random error)—组内误差(within-group error)
由于随机因子造成的误差,也简称为误差(error)
数据的误差用平方和(sum of squares)表示,记为SS
总平方和(sum of squares for total),记为SST
反映全部数据总误差大小的平方和
例如,全部30个地块的产量之间的误差平方和就是总平方和,它反映了全部产量的总离散程度。
处理平方和(treatment sum of squares),记为SSA
反映处理误差大小的平方和。(例如,不同品种之间产量的误差平方和就是处理平方和)
也称为组间平方和(between-group sum of squares)
误差平方和(sum of squares of error),记为SSE
反映随机误差大小的平方和称为误差平方和
也称为组内平方和(within-group sum of squares)
全部数据的总误差平方和被分解成两部分一部分是处理平方和SSA,另一部分是误差平方和SSE。很显然,这三个误差平方和的关系为:SST=SSA+SSE。
数据误差的来源及其分解过程可用下面的图来表示:
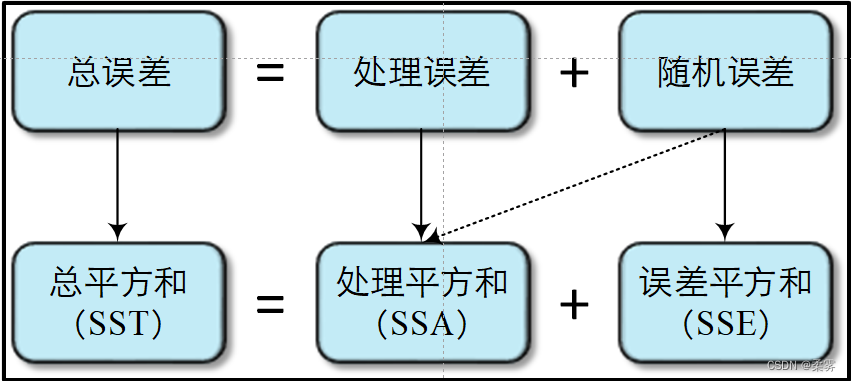
方差分析的基本原理就是要分析数据的总误差中处理误差是否显著存在。如果处理(小麦品种)对观测数据(产量)没有显著影响,意味着处理误差不显著。这时,每种处理所对应的总体均值(i)应该相等。
如果存在处理误差,每种处理所对应的总体均值(i)至少有一对不相等
就本例而言,在只考虑品种一个因子的情况下,方差分析也就是要检验下面的假设

单因子方差分析
数学模型
设因子A有I种处理比如品种有(“品种1”、“品种2”、“品种3”)3种处理,单因子方差分析可用下面的线性模型来表示
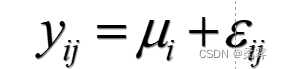




效应检验
设因子A有I种处理,单因子方差分析要检验的假设为:
H0 :ai = 0 (i=1,2,…,I)
没有处理效应
H1 :ai 至少有一个不等于0
有处理效应
为获得上述检验的统计量,首先需要计算处理平方和SSA、误差平方和SSE,然后将各平方和除以相应的自由度df,以消除观测数据多少对平方和大小的影响,其结果称为均方(mean square),也称为方差。
最后,将处理均方(MSA)除以误差均方(MSE),即得到用于检验处理效应的统计量F。这一计算过程可以用方差分析表的形式来表示。下表显示了单因子方差分析表的一般形式:
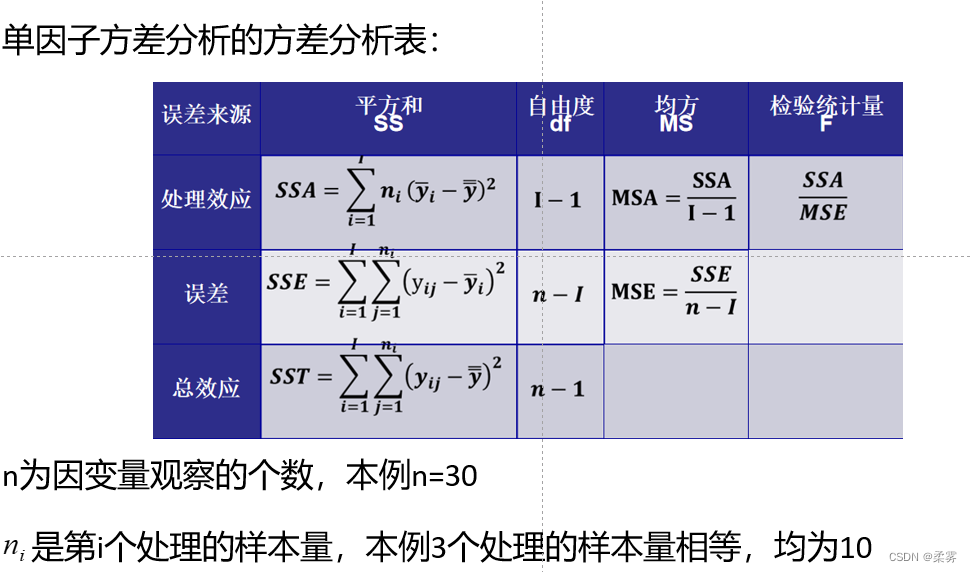

有了统计量,就可以根据P值做出决策:若P<α,拒绝H0,αi不全为0,表示处理效应显著(因子对观察值有显著影响)。
例题:
(数据:example8_2. RData)沿用例7-1。检验小麦品种对产量的影响是否显著(α=0.05)
解:设小麦品种对产量的影响效应分别为a1(品种1)、a2(品种2)、a3(品种3)

为使用R做方差分析,需要将短格式数据(example8_1)转为长格式数据,并存为 example8_2。R代码和结果如下所示
# 将表8-1的短格式数据转为长格式数据
load("C:/example/ch8/example8_1.RData")
example8_1<-cbind(example8_1,id=factor(1:10))
library(reshape)
example8_2<-melt(example8_1,id.vars=c("id"), variable_name="品种")
example8_2<-rename(example8_2,c(id="地块",value="产量"))
save(example8_2,file="C:/example/ch8/example8_2.RData")
example8_2

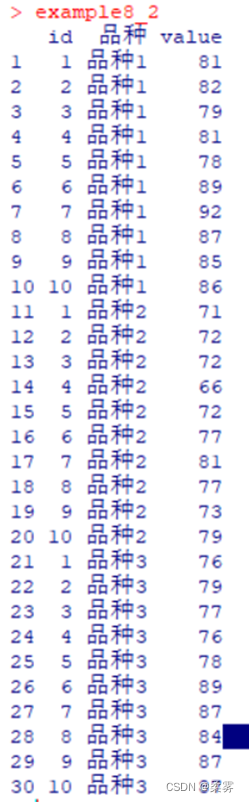
melt()函数用法:把数据转变成长格式数据
melt(data,id.vars,measure.vars,variable.name,value.name)
id.vars:标识变量(依旧在列上,位置保持不变的变量)
measure.vars:度量变量(需要放进同一列的变量)
variable.name:为新列变量取名
value.name:对应值所在的变量名
为便于理解方差分析的结果,可以先对样本数据做一些描述性分析。首先绘制3个品种产量的箱线图,并计算各样本的均值和标准差,观察不同品种产量之间的差异。R代码和结果如下所示
#绘制3个品种数据产量的箱线图
load("C:/example/ch8/example8_2.RData")
attach(example8_2)
boxplot(产量~品种,data=example8_2,col="gold",main="",ylab="产量", xlab="品种")
#计算描述统计量
my_summary<-function(x){with(x,data.frame("均值"=mean(产量),"标准差"=sd(产量),n=length(产量)))}
library(plyr)
ddply(example8_2,.(品种),my_summary)
#ddply()函数用于对data.frame进行分组统计
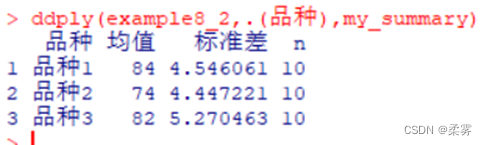
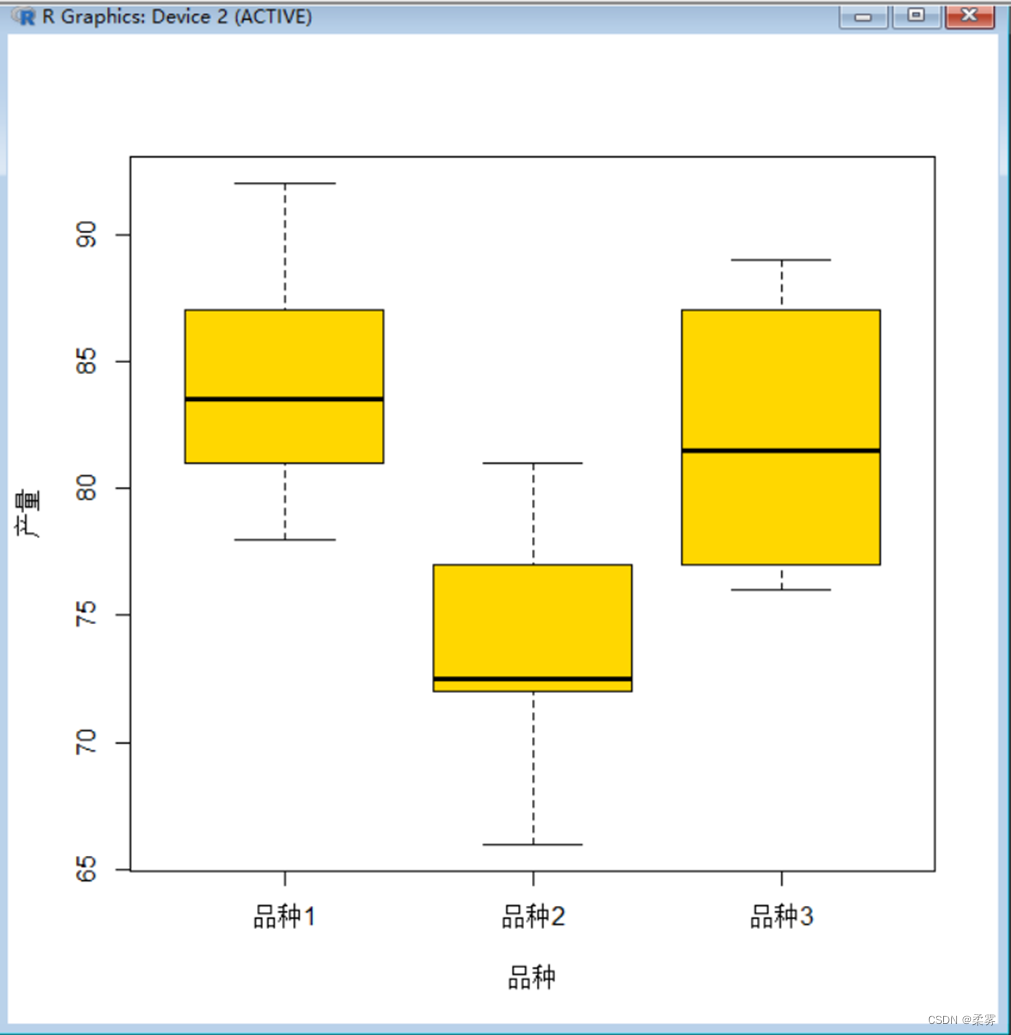
从箱线图中可以看出,品种2的产量明显低于品种1和品种3,而品种1和品种3的产量差异似乎不大。从3个品种产量的均值也可见其差异。但要想知道不同品种之间的产量差异是否显著,还需要做方差分析。R代码和结果如下所示:
#方差分析表
attach(example8_2)
model_1w<-aov(产量~品种)
summary(model_1w)

#方差分析模型的参数估计
model_1w$coefficients

注:函数aov( formula,data=NULL,)用于拟合方差分析模型。参数 formula用于指定模型形式;data为数据框。单因子方差分析模型的R表达式为:y~A,其中y为因变量,A为因子。
方差分析表显示了品种效应和随机效应的平方和(Sum Sq)、自由度(Df)、均方(Mean Sq)、检验统计量值(F value)、检验的P值(Pr(>F))。由于P=0.000158<0.05,拒绝原假设,表示αi(i=1,2,3)至少有一个不等于0,这意味着品种对产量的影响效应显著。

练习
1、一家牛奶公司有4台机器装填牛奶,每桶的容量为4L。下面是从4台机器中抽取的装填量样本数据。
检验机器对装填量是否有显著差异?
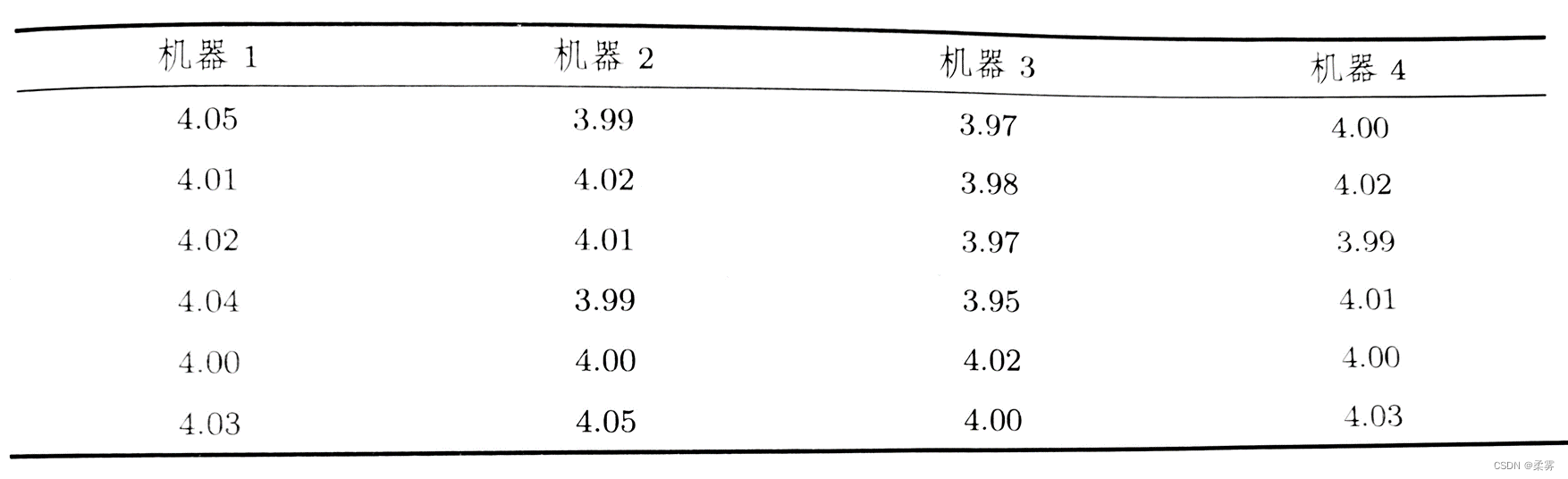
解:提出假设:
H0: 机器对装填量的影响不显著
H1:机器对装填量的影响显著
#绘制出箱线图
load("C:/example/ch8/exercise8_1.RData")
exercise8_1
attach(exercise8_1)
boxplot(填装量~机器,data=exercise8_1,col="gold",main="",ylab="填装量", xlab="机器")
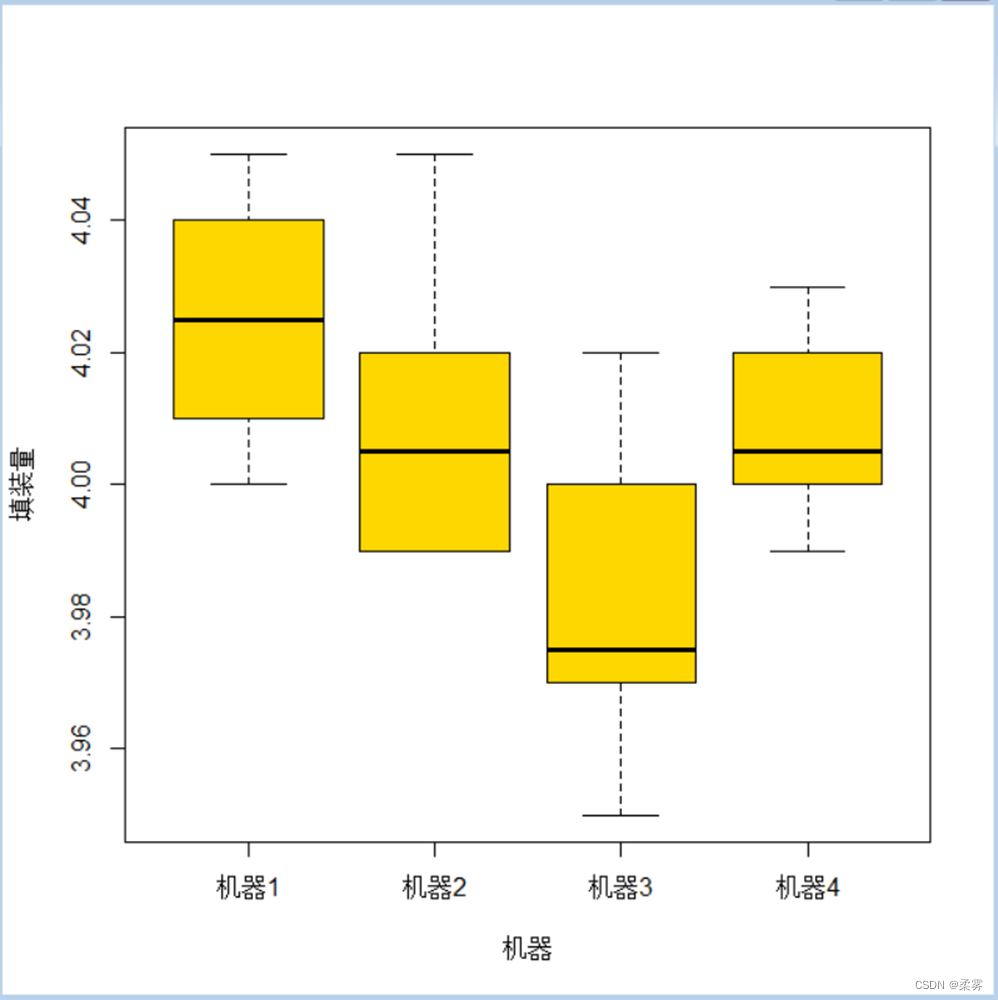
#方差分析表
attach(example8_2)
model_1w<-aov(填装量~机器)
summary(model_1w)
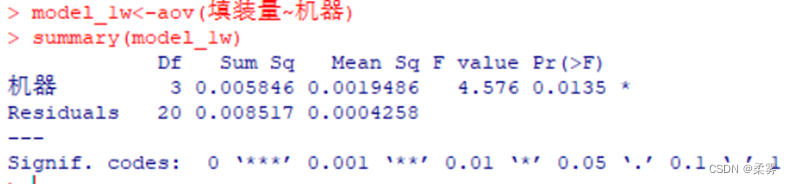
方差分析表显示了机器效应和随机效应的平方和(Sum Sq)、自由度(Df)、均方(Mean Sq)、检验统计量值(F value)、检验的P值(Pr(>F))。由于P=0.0135<0.05,拒绝原假设,机器对填装量的影响效应显著。
#方差分析模型的参数估计
model_1w$coefficients