Vue-Router是Vue.js官方的路由管理器，它可以帮助我们快速构建单页应用程序（SPA）。除了常见的路由功能外，Vue-Router还支持使用路由元信息来管理和控制路由。路由元信息是可以附加到路由上的自定义属性，它可以帮助我们实现一些特殊的逻辑或者权限控制。

一、什么是路由元信息？
路由元信息是指附加在每个路由上的属性和值。我们可以根据这些元信息来控制路由的行为。比如，我们可以在路由元信息中添加一个属性用来控制是否需要登录才能访问该路由。

二、如何使用路由元信息？

1，声明路由元信息
在定义路由时，可以通过meta字段添加路由元信息。例如：

 

在上述代码中，我们为了'/home'路由添加了一个含有requiresAuth属性的meta字段，这意味着/home页面需要进行身份验证才能访问，而/about页面不需要。

2，判断路由元信息并做出相应处理
我们可以在路由导航守卫中根据路由元信息来判断是否需要进行某些操作。导航守卫是在路由跳转时触发的钩子函数。例如，在全局前置守卫中我们可以进行权限验证，判断用户是否有访问某个路由的权限：

 

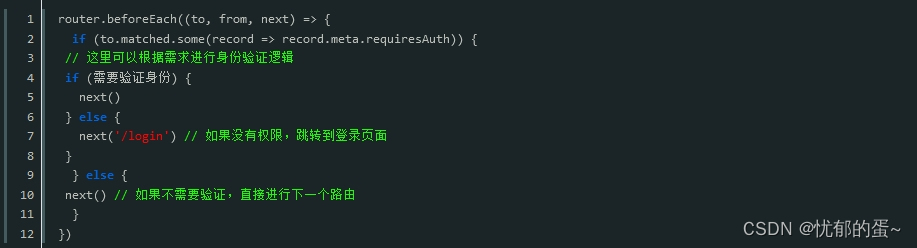
在上述代码中，我们首先判断当前路由的元信息中是否有requiresAuth属性，如果有，则进行身份验证逻辑，如果没有，则直接进行下一个路由。

3，在组件中获取路由元信息
一旦设置了路由元信息，我们可以通过$route.meta来获取它。例如，在组件中我们可以通过以下方式来获取/about路由的元信息：

在上述代码中，我们使用this.$route来获取当前路由信息，并通过$route.meta.requiresAuth来获取requiresAuth属性的值。

总结：
通过使用路由元信息，我们可以很方便地控制路由的行为和进行权限控制。无论是全局导航守卫还是在局部组件中，我们都可以根据路由元信息来决定是否允许用户访问某个页面。使用Vue-Router的路由元信息功能，可以使我们的应用程序更加灵活和安全