Python Kdtree 使用示例

一、关于 KDTree

• 点云数据主要是， 表征 目标表面 的海量点集合， 并不具备传统实体网格数据的几何拓扑结构。
• 点云数据处理中最为核心的问题就是， 建立离散点间的拓扑关系， 实现基于邻域关系的快速查找。
• KDTree，即k-dimensional tree，是一种高维索引树形数据结构，常用于在大规模的高维数据空间进行最近邻查找(Nearest Neighbor)和近似最近邻查找(Approximate Nearest Neighbor)，例如图像检索和识别中的高维图像特征向量的K近邻查找与匹配。
• KDTree的每一级(level)在指定维度上分开所有的子节点。在树的根部，所有的子节点在第一个维度上被分开(第一维坐标小于根节点的点将被分在左边的子树中，大于根节点的点将被分在右边的子树中)。树的每一级都在下一个维度上分开，所有其他的维度用完之后就回到第一个维度，直到你准备分类的最后一个树仅仅由有一个元素组成。

二、关于最近邻搜索

给定点p，查询数据集中与其距离最近点的过程即为最近邻搜索。

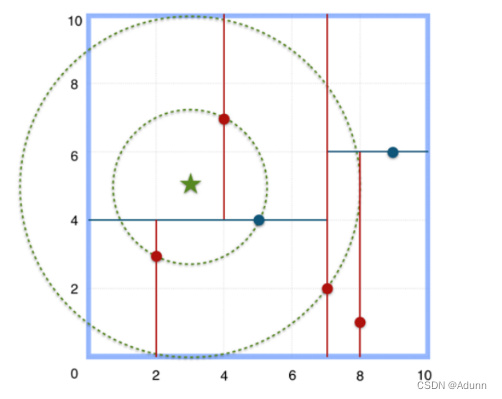
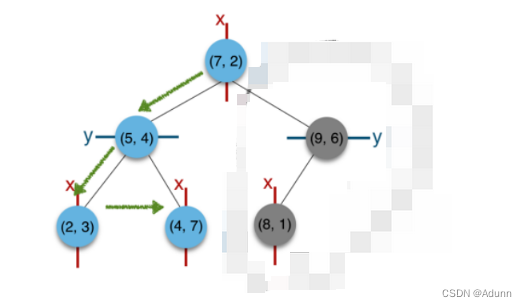
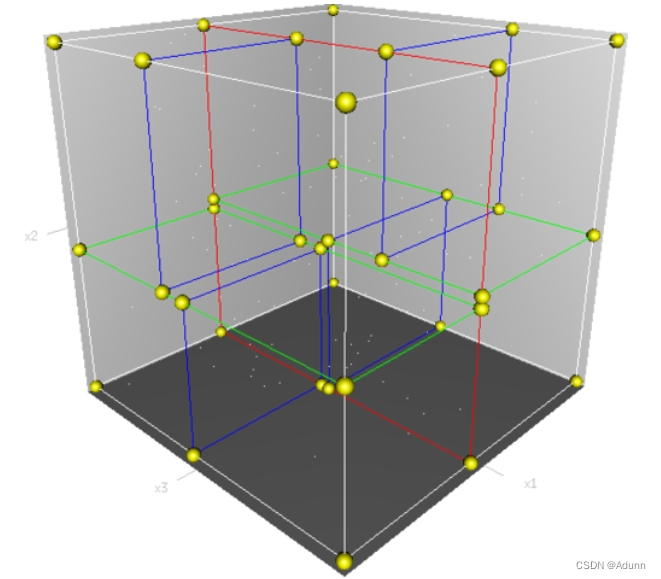
如在构建好的k-d tree上搜索(3,5)的最近邻时：

（1）首先从根节点(7,2)出发，将当前最近邻设为(7,2)，对该k-d tree作深度优先遍历。以(3,5)为圆心，其到(7,2)的距离为半径画圆（多维空间为超球面），可以看出(8,1)右侧的区域与该圆不相交，所以(8,1)的右子树全部忽略。

（2） 接着走到(7,2)左子树根节点(5,4)，与原最近邻对比距离后，更新当前最近邻为(5,4)。以(3,5)为圆心，其到(5,4)的距离为半径画圆，发现(7,2)右侧的区域与该圆不相交，忽略该侧所有节点，这样(7,2)的整个右子树被标记为已忽略。

（3） 遍历完(5,4)的左右叶子节点，发现与当前最优距离相等，不更新最近邻。所以(3,5)的最近邻为(5,4)。

三、复杂度分析

• 新增节点：平均复杂度为O(logn)，最坏复杂度O(n)；
• 删除节点：平均复杂度为O(logn)，最坏复杂度O(n)；
• 最近邻搜索： 平均复杂度为O(logn) ，最坏复杂度O(n)；

四、python实现的简化版构建k-d tree（k=2）

# -*- coding:utf-8 -*-

import numpy as np


class KdNode:
    """kd tree中的一个点，属性包括
    x:这个点的x值
    y:这个点的y值
    level:第几级树
    right:右节点
    left：左节点"""
    def __init__(self, x, y, level):
        self.x = x
        self.y = y
        self.level = level
        self.right = None
        self.left = None


class KdTree:
    def __init__(self):
        self._node = None
        # 初始化一个节点为None

    def insert(self, x, y):
        if self._node is None:
            self.add(x, y, node=self._node, level=1)
            # 添加根节点
        else:
            self.add(x, y, node=self._node, level=2)
            # 其他节点

    def add(self, x, y, node, level):
        if node is None:
            # 如果是添加根节点
            print('所创建的k-d树还未创建根节点，将自动把(%.4f,%.4f)设为根节点' % (x, y))
            self._node = KdNode(x, y, level)

        elif level % 2 == 1:
            if node.y < y:
                if node.right is None:
                    node.right = KdNode(x, y, level)
                else:
                    self.add(x, y, node.right, level + 1)
            elif node.y >= y:
                if node.left is None:
                    node.left = KdNode(x, y, level)
                else:
                    self.add(x, y, node.left, level + 1)

        elif level % 2 == 0:
            if node.x < x:
                # 大的放在右边
                if node.right is None:
                    # 如果右边还没有节点
                    node.right = KdNode(x, y, level)
                else:
                    # 如果右边有节点了，以已经存在了的这个结点为父节点，向下一级划分
                    self.add(x, y, node.right, level + 1)
            elif node.x >= x:
                # 小的或者等的放在左边
                if node.left is None:
                    node.left = KdNode(x, y, level)
                else:
                    self.add(x, y, node.left, level + 1)

    def append_infix(self, node, x, y, level):
        """中序遍历
        若树非空，则依次执行如下操作：
        ⑴遍历左子树；
        ⑵访问根结点；
        ⑶遍历右子树。"""
        if node is None:
            return

        self.append_infix(node.left, x, y, level)
        x.append(node.x)
        y.append(node.y)
        level.append(node.level)
        self.append_infix(node.right, x, y, level)

    def append_pre(self, node, x, y, level):
        """先序遍历
        若二叉树非空，则依次执行如下操作：
        ⑴ 访问根结点；
        ⑵ 遍历左子树；
        ⑶ 遍历右子树。"""
        if node is None:
            return

        x.append(node.x)
        y.append(node.y)
        level.append(node.level)
        self.append_pre(node.left, x, y, level)
        self.append_pre(node.right, x, y, level)

    def append_post(self, node, x, y, level):
        """后序遍历
        若二叉树非空，则依次执行如下操作：
        ⑴遍历左子树；
        ⑵遍历右子树；
        ⑶访问根结点。"""
        if node is None:
            return

        self.append_post(node.left, x, y, level)
        self.append_post(node.right, x, y, level)
        x.append(node.x)
        y.append(node.y)
        level.append(node.level)

    def print_kd_tree(self, traversal):
        x = []
        y = []
        level = []

        if traversal == "infix":
            self.append_infix(self._node, x, y, level)
        elif traversal == "pre":
            self.append_pre(self._node, x, y, level)
        elif traversal == "post":
            self.append_post(self._node, x, y, level)
        else:
            print("Parameter error")

        for each in range(len(x)):
            print("(%.4f, " % x[each] + "%.4f, " % y[each] + "%.d)" % level[each])


if __name__ == "__main__":
    my_kd_tree = KdTree()

    x_list = np.random.uniform(0, 10, 10)
    # 随机生成10个（0, 10）的浮点数
    y_list = np.random.uniform(0, 10, 10)

    for i in range(len(x_list)):
        my_kd_tree.insert(x_list[i], y_list[i])
        # 每来一个新的结点，都是从根节点开始，顺着向下找自己的位置
    my_kd_tree.print_kd_tree("infix")