题目描述:
小明有一个数组,他想从数组任意元素开始向后遍历,找出所有上升子序列,并计算出最长的上升子序列的长度。
数据范围:
每组数据长度满足 1≤n≤200 1≤n≤200 , 数据大小满足 1≤val≤350 1≤val≤350
输入描述:
数据共2行,第1行先输入数组的个数,第2行再输入梅花桩的高度
输出描述:
输出一个结果
示例:
假设数组为:6,2,3,7,9,0,10
若选择第一个元素6作为起点,则最长的上升子序列为:6,7,9,10;长度为4
若选择第二个元素2作为起点,则最长的上升子序列为:2,3,7,9,10;长度为5
若选择第三个元素3作为起点,则最长的上升子序列为:3,7,9,10;长度为4
若选择第四个元素7作为起点,则最长的上升子序列为:7,9,10;长度为3
若选择第五个元素9作为起点,则最长的上升子序列为:9,10;长度为2
若选择第六个元素0作为起点,则最长的上升子序列为:0,10;长度为2
若选择第七个元素10作为起点,则最长的上升子序列为:10;长度为1
用一个矩阵表示上述示例信息:
6,2,3,7,9,0,10
6,x,x,7,9,x,10
x,2,3,7,9,x,10
x,x,3,7,9,x,10
x,x,x,7,9,x,10
x,x,x,x,9,x,10
x,x,x,x,x,0,10
x,x,x,x,x,x,10
x,x,x,x,x,x,x
站在每一个元素的位置考虑,若当前位置的元素比其前边的元素要大,则形成了一种升序的关系。
如:
站在元素6的位置考虑,它前边没有元素,所以它本身就构成了一个上升子序列。
站在元素2的位置考虑,它前边有一个元素,但是前边的元素6比它本身要大,所以它也只能用元素本身构成一个升序子序列。
站在元素3的位置考虑,元素6肯定无法与元素3构成升序的关系,但是元素2可以。所以站在元素3的位置考虑,升序子序列为2,3。以此类推。
我们考虑一个位置的元素是否与之前的元素构成升序关系,那么直接从下标0遍历到当前元素位置-1的位置,用当前位置元素与过往元素逐一比较就能辨别出是否含有升序关系。如下图,可以明显的发现,考虑第n个位置的元素是否与0~n-1位置的元素构成升序子序列时,有多个重复的子过程。
即考虑6的时候,前方无元素
考虑2的时候,要考虑前方的6
考虑3的时候,要考虑前方的6和2…
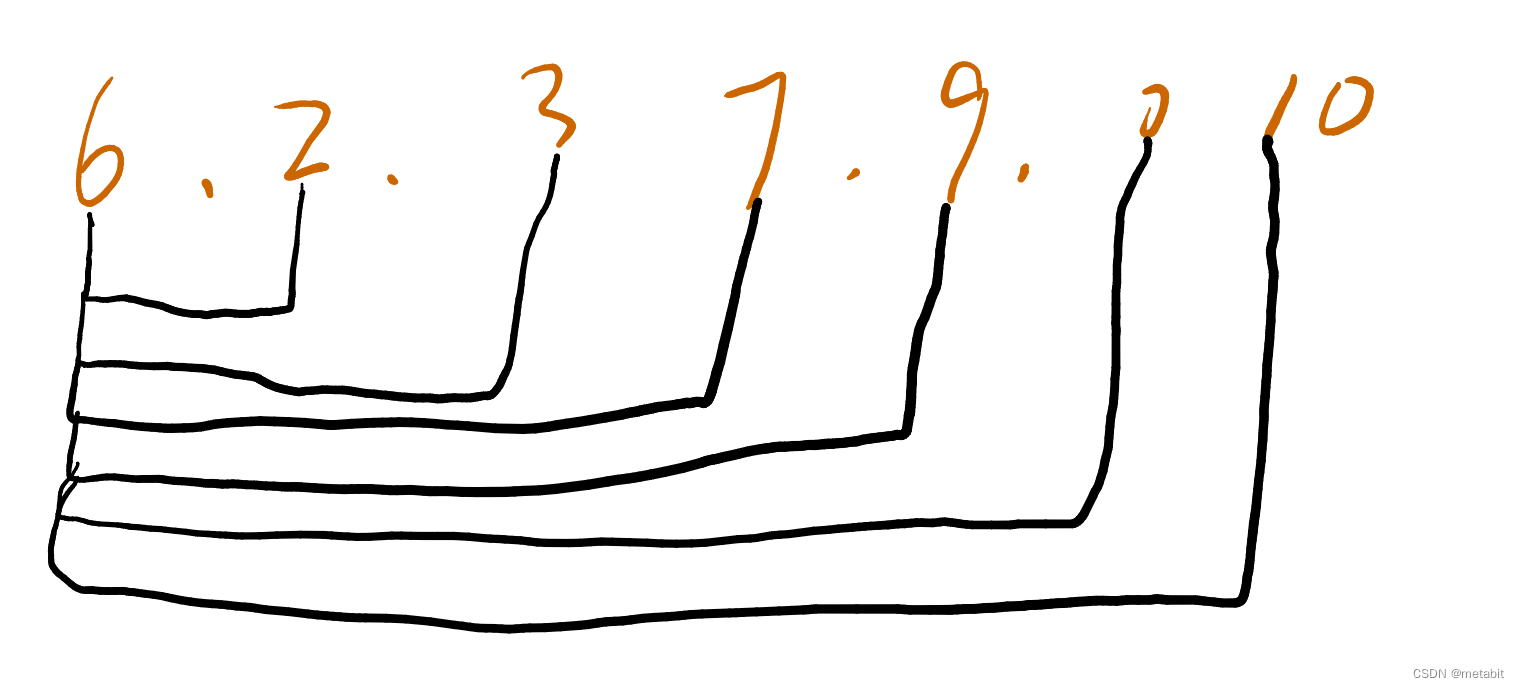 那么现在使用递归设计一套流程,计算以每个位置为结尾的子数组包含多少个上升子序列的元素,并取最大的元素个数。
那么现在使用递归设计一套流程,计算以每个位置为结尾的子数组包含多少个上升子序列的元素,并取最大的元素个数。
package main
import (
"fmt"
)
func main() {
n := 0
fmt.Scan(&n)
arr := make([]int, 0, n)
tmp := 0
for i := 0; i < n; i++ {
fmt.Scan(&tmp)
arr = append(arr, tmp)
}
result := -0x3f3f3f3f
for i := 0; i < len(arr); i++ {
tmp := process(arr, i)
if tmp > result {
result = tmp
}
}
fmt.Println(result)
}
func process(arr []int, index int) (result int) {
if index == 0 {
return 1
}
for i := 0; i < index; i++ {
if arr[index] > arr[i] {
tmp := process(arr, i)
if tmp > result {
result = tmp
}
}
}
return result + 1
}
因为有多个重复子过程,所以可将上述流程优化成记忆化搜索。
package main
import (
"fmt"
)
func main() {
n := 0
fmt.Scan(&n)
arr := make([]int, 0, n)
tmp := 0
for i := 0; i < n; i++ {
fmt.Scan(&tmp)
arr = append(arr, tmp)
}
cache := make([]int, len(arr))
result := -0x3f3f3f3f
for i := 0; i < len(arr); i++ {
tmp := process(arr, cache, i)
if tmp > result {
result = tmp
}
}
fmt.Println(result)
}
func process(arr []int, cache []int, index int) (result int) {
if index == 0 {
return 1
}
for i := 0; i < index; i++ {
var tmp int
if arr[index] > arr[i] {
if cache[i] != 0 {
tmp = cache[i]
} else {
tmp = process(arr, cache, i)
cache[i] = tmp
}
if tmp > result {
result = tmp
}
}
}
return result + 1
}
有了记忆化搜索,我们何不将其优化成动态规划的形式,将递归换成循环即可。如下:记忆化搜索改写成动态规划。
package main
import (
"fmt"
)
func main(){
n := 0
fmt.Scan(&n)
arr := make([]int,0,n)
tmp := 0
for i := 0; i < n; i++ {
fmt.Scan(&tmp)
arr = append(arr, tmp)
}
// 6
// 2 5 1 5 4 5
// 2 x x x 4 5
// x 5 x x x x
// x x 1 x 4 5
// x x x 5 x x
// x x x x 4 5
// x x x x x 5
cache := make([]int,n)
for i := 0; i < n; i++ {
cache[i] = 1
}
res := 0
for i := 1; i < n; i++ {
for j := 0; j < i; j++ {
if arr[i] > arr[j] {
cache[i] = max(cache[i], cache[j]+1)
}
}
if cache[i] > res {
res = cache[i]
}
}
fmt.Println(res)
}
func max(a, b int) int {
if a > b {
return a
}
return b
}