---

前言

本篇文章继续对总体方差的检验进行介绍。

---

总体方差的检验

一个总体方差的检验

在生产和生活的许多领域，方差的大小是否适度是需要考虑的一个重要因素。一个方差大的产品意味着其质量或性能不稳定。相同均值的产品，方差小的自然要好些。与总体方差的区间估计类似，一个总体方差的检验也是使用 分布。此外，总体方差的检验，不论样本量n是大还是小，都要求总体服从正态分布。检验统计量为

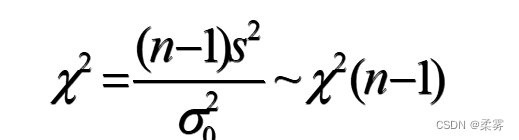
对于设定的显著性水平 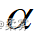，双侧检验的拒绝域如下图所示。对于单侧检验拒绝域在分布一侧的尾部

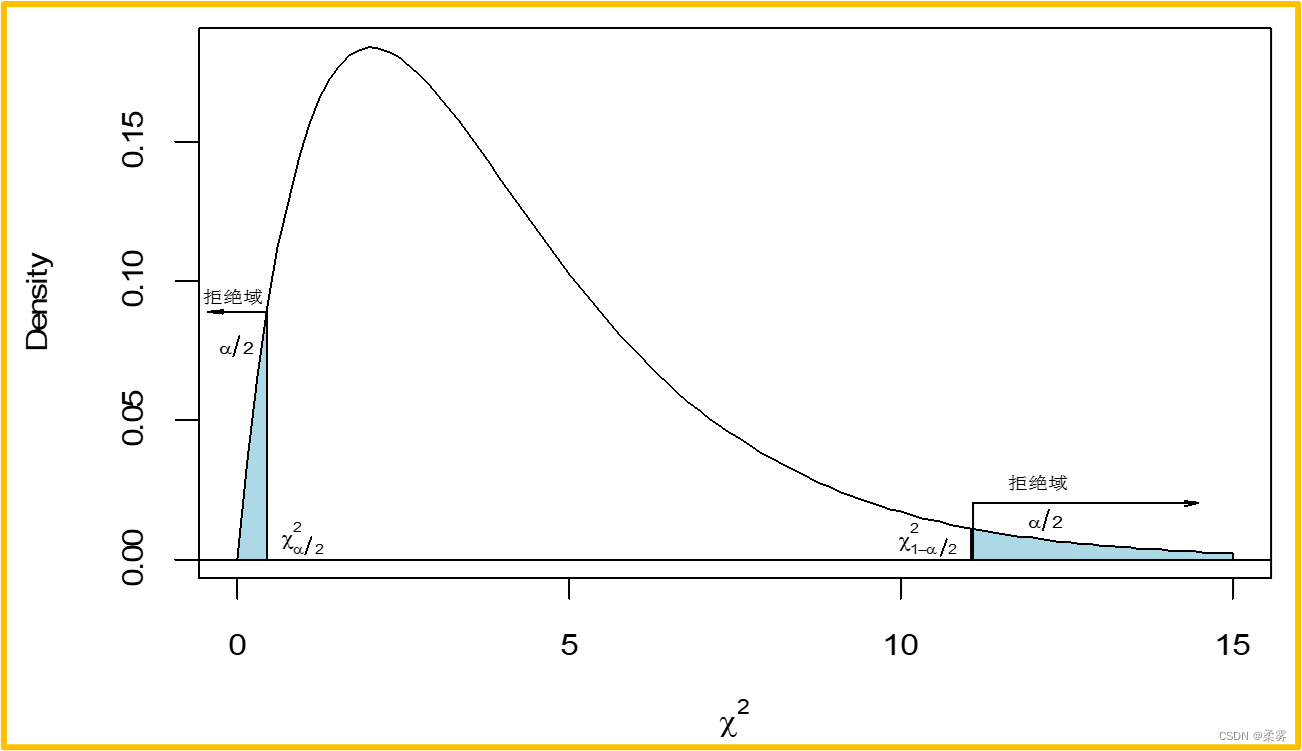
例题：
啤酒生产企业采用自动生产线灌装啤酒，每瓶的填装量为640ml，但由于受某些不可控因素的影响，每瓶的填装量会有差异。如果 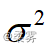很大，会出现填装量太多或太少的情形，这样，要么生产企业不划算，要么消费者不满意。假定生产标准规定每瓶填装量的方差不应超过16。企业质检部门抽取了10瓶啤酒进行检验，得到的样本数据如下。检验填装量的方差是否符合要求（ =0.05）
638.3 642.0 640.4 641.1 637.2 643.3 643.7 640.5 639.8 644.2

sigma.test(x,sigmasq= ,alternative=" ")

load("C:/example/ch6/example6_11.RData")
library(TeachingDemos)
sigma.test(example6_11$填装量,sigmasq=16,alternative="greater")

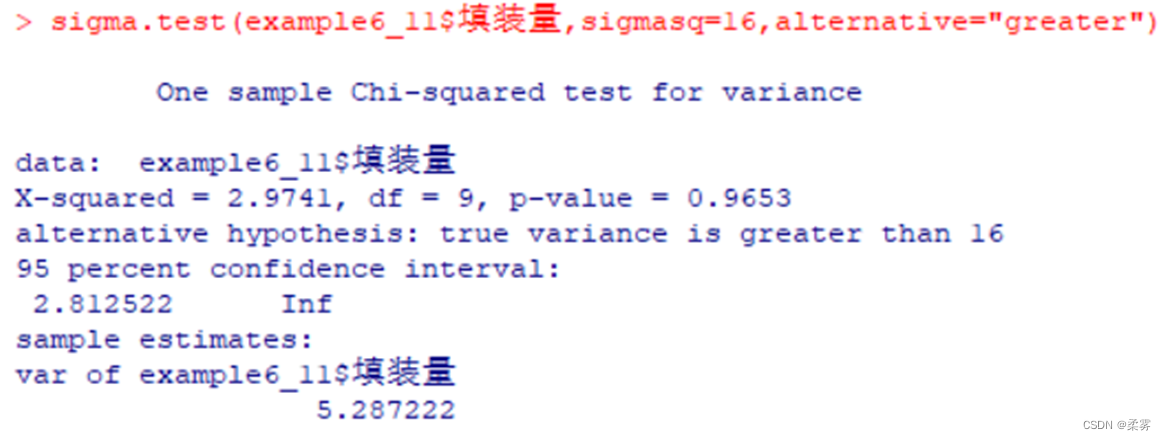
两个总体方差比的检验

（数据： example6_6. RData）沿用例6-6。检验两家企业灯泡使用寿命的方差是否有显著差异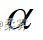（ =0.05）

load("C:/example/ch6/example6_6.RData")
var.test(example6_6[,1],example6_6[,2],alternative="two.sided")

非参数检验

以上介绍的参数检验（如t检验、F检验等）通常是在假定总体服从正态分布或总体分布形式已知的条件下进行的、而且要求所分析的数据是数值的。
当总体的概率分布形式未知、或者无法对总体的概率分布做出假定时，参数检验方法往往会失效，这时可采用非参数检验。非参数检验方法不仅对总体的分布要求很少，对数据类型的要求也比参数检验宽松。当数据不适合用参数检验时，非参数检验往往能得出理想的结果。本篇主要介绍总体分布的检验以及几种常用的参数检验的替代方法。

总体分布的检验

在实际问题中，除了关心总体参数外，还会关心总体的分布，比如，总体是否服从正态分布，两个总体的分布是否相同，等等。
介绍检验正态性的几种方法，它是根据样本数据检验总体是否服从正态分布，或者说样本数据是否来自正态总体，检验方法有图示法和检验法。图示法主要有Q-Q图和P-P图，检验法主要有 Shapiro-Wilk检验和 Kolmogorov- Smirnov检验(K-S检验)等。

正态性检验的图示法

判断数据是否服从正态分布的描述性方法之一，就是画出数据频数分布的直方图或茎叶图，若数据近似服从正态分布，则图形的形状与正态曲线应该相似。但实际中更常用的方法是绘制样本数据的正态概率图( normal probability plots)。正态概率图有两种画法，一种称为Q-Q图( quantile-quantile plot)，一种称为P-P图( probabilit probability plot)。
Q-Q图是根据观测值的实际分位数与理论分布(如正态分布)的分位数的符合程度绘制的，有时也称为分位数-分位数图；P-P图则是根据观测数据的累积概率与理论分布(如正态分布)的累积概率的符合程度绘制的。
下图是用R模拟的几种不同分布的Q-Q图

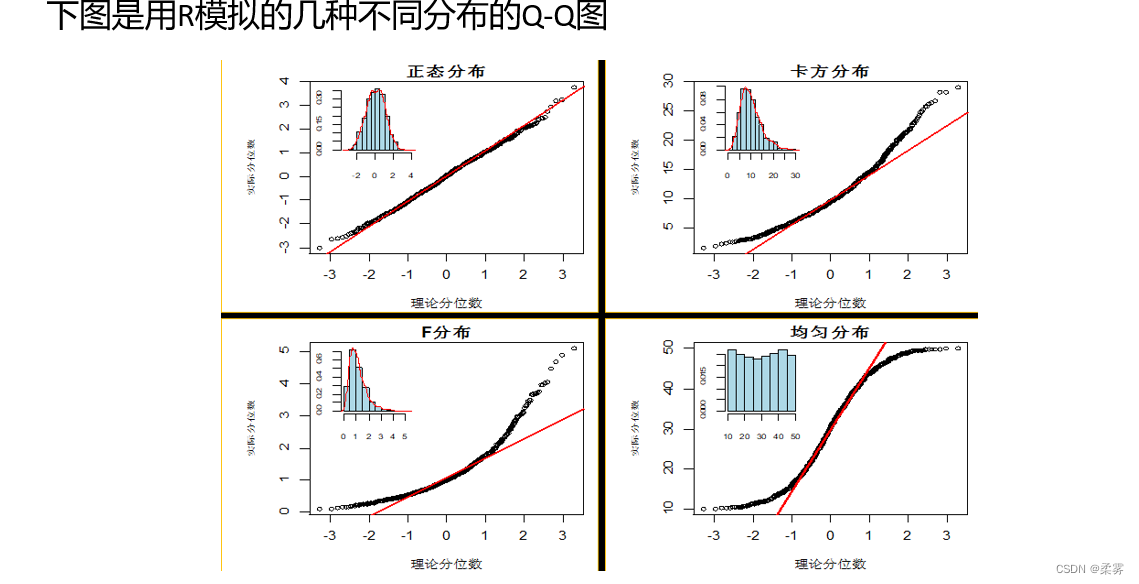
例题：
(数据: example6_3.RData)沿用例6-3。会制Q-Q图和P-P图，检验该城市每立方米空气中的PM2.5是否服从正态分布。

#  绘制Q-Q图
 qqnorm(x,xlab=" ",ylab=" ",datax=TRUE,main="正态Q-Q图")
 qqline(x,datax=TRUE,col="")
 
# 绘制P-P图
 f<-ecdf(x)
 p1<-f(x)#y<- ecdf(x)；y(x)；plot(x,y(x), ylab = "ECDF(x)")
 p2<-pnorm(x,mean(x),sd(x)) 
 plot(p1,p2,xlab="观测的累积概率",ylab="期望的累积概率",main="正态P-P图")
 abline(a=0,b=1,col=" ")

#  绘制Q-Q图
 load("C:/example/ch6/example6_3.RData")
 par(mfrow=c(1,2),cex=0.8,mai=c(0.7,0.7,0.2,0.1))
 qqnorm(example6_3$PM2.5值,xlab="期望正态值",ylab="观测值",datax=TRUE,main="正态Q-Q图")
 qqline(example6_3$PM2.5值,datax=TRUE,col="red")
 
# 绘制P-P图
 f<-ecdf(example6_3$PM2.5值)
 p1<-f(example6_3$PM2.5值)#y<- ecdf(x)；y(x)；plot(x,y(x), ylab = "ECDF(x)")
 p2<-pnorm(example6_3$PM2.5值,mean(example6_3$PM2.5值),sd(example6_3$PM2.5值)) 
 plot(p1,p2,xlab="观测的累积概率",ylab="期望的累积概率",main="正态P-P图")
 abline(a=0,b=1,col="red")

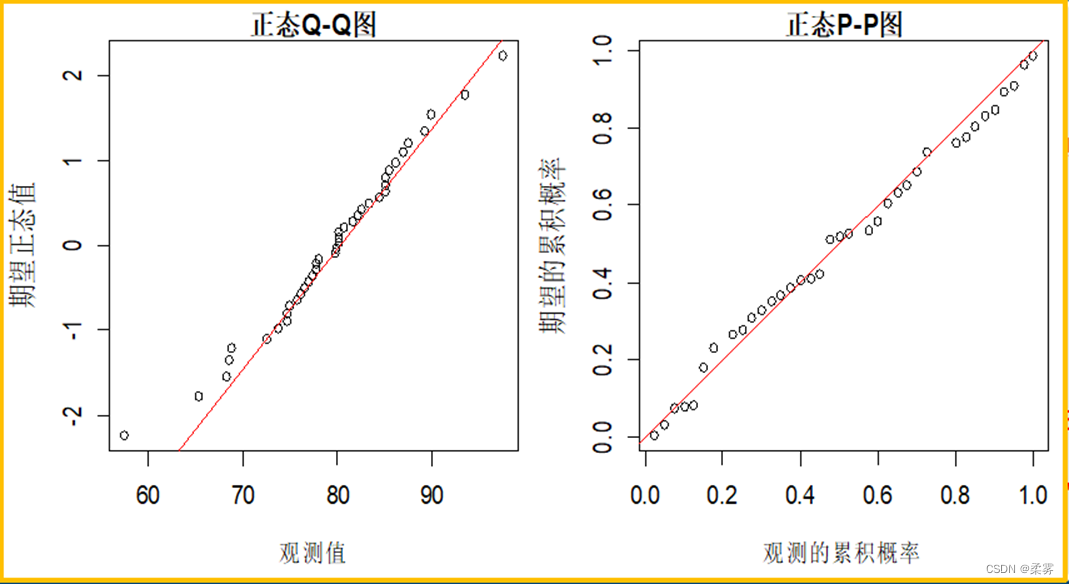
图中的直线表示理论正态分布线，各观测点越靠近直线，且呈随机分布，表示数据越接近正态分布。从图中可以看出，各观测点大致围绕在一条直线周围随机分布，可以说该城市每立方米空气中的PM2.5基本上服从正态分布。
在分析正态概率图时，最好不要用严格的标准去衡量数据点是否在理论直线上，只要各点近似在一条直线周围随机分布即可。而且当样本量比较小时正态概率图中的点很少，提供的正态性信息很有限，因此样本量应尽可能大。

Shapiro-Wilk和K-S正态性检验

当样本量较小时，正态概率图的应用就会受到限制，这时可以使用标准的统计检验方法。检验的原假设是总体服从正态分布。
如果检验获得的P值小于指定的显著性水平，则拒绝原假设，表示总体不服从正态分布；如果P值较大不能拒绝原假设，可以认为总体满足正态分布。正态性的检验方法有很多、这里只介绍两种常用的检验方法，即 Shapiro-Wilk检验和K-S检验。

Shapiro-Wilk检验
Shapiro-Wilk检验是S.Shapiro和M.Wilk于1965年提出的，该检验是用顺序统计量W来检验分布的正态性。 Shapiro-wilk检验的具体步骤如下：
首先，对研究的总体提出如下假设：
H0：总体服从正态分布；H1：总体不服从正态分布
然后，按下列公式计算检验统计量W：

(数据: example6_4.RData) 沿用例6-4。用 Shapiro-wilk方法检验该企业生产的砖的厚度是否服从正态分布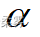（ =0.05）。

load("C:/example/ch6/example6_4.RData")
shapiro.test(example6_4$厚度)

结论：在该项检验中，W=0.91377，P=0.07522，由于P>0.05，不拒绝原假设，没有证据显示该企业生产的砖的厚度不服从正态分布。

K-S检验
Shapiro–Wilk检验只适用于小样本场合（3≤n<50），当样本量较大时，可使用K-S检验。该检验既可以用于大样本，也可以用于小样本。
K-S检验用来检验总体是否服从某个已知的理论分布。该检验是将某一变量的累积分布函数与特定的分布函数进行比较，检验其拟合程度。设总体的累积分布函数为F(x)，已知的理论分布函数为F0(x)，则检验的原假设和备择假设为：


K-S检验
如果H0成立，每次抽样得到的D值应当不会与0偏离太远，否则就应拒绝H0。对于设定的显著性水平 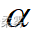，若检验统计量D（或z）对应的概率小于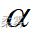，则拒绝H0，表示总体与指定的理论分布差异显著。
K-S检验要求样本数据是连续的数值数据，而且要求理论分布已知。比如，要检验的样本数据是否来自μ=100， =10的正态总体，即 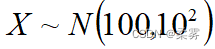。当总体均值和方差未知时，可以用样本均值 和方差 来代替
K-S检验的函数为：ks.test（x，y，…）.参数x为向量或数据框；y指定分布，pnom表示要检验的是正态分布；mean和sd是正态分布的均值和标准差。

(数据: example6_4.RData) 沿用例6-4。用K-S方法检验该企业生产的砖的厚度是否服从正态分布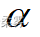（ =0.05）。
ks.test（x，y，…）.参数x为向量或数据框；y指定分布；

load("C:/example/ch6/example6_4.RData")
ks.test(example6_4$厚度,"pnorm", mean(example6_4$厚度), sd(example6_4$厚度))

结论：在该项检验中，D=0.23538，P=0.2178，由于P>0.05，不拒绝H0，没有证据显示该企业生产的砖的厚度不服从正态分布。
注：K-S检验的函数为：ks.test（x，y，…）.参数x为向量或数据框；y指定分布，pnom表示要检验的是正态分布；mean和sd是正态分布的均值和标准差。

由于 Shapiro-Wilk检验和K-S检验对正态性偏离十分敏感，因此当样本数据轻微偏离正态分布时，这些检验往往也会导致拒绝原假设。当某些分析对正态性的要求相对宽松时，应谨慎使用这些检验。

总体位置参数的检验

总体位置参数的检验是参数检验的一种替代方法。当只有一个总体时，通常关心总体的某个位置参数（如中位数）是否等于假设值，检验方法主要是 Wilcoxon（威尔科克森）符号秩检验。当有两个总体时，通常关心两个总体的位置参数是否相同。对于独立样本，采用Mann- Whitney(曼-惠特尼)检验；对于配对样本，则采用配对样本的 Wilcoxon符号秩检验。
秩(rank)的概念：
秩就是一组数据按照从小到大的顺序排列之后，每一个观测值所在的位置
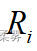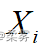用一般符号R来表示，假定一组数据 按照从小到大的顺序排列， 在所有观测值中排第 位，那么 的秩即为 。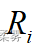

也是一个统计量，它测度的是数据观测值的相对大小，大多数非参数检验方法正是利用秩的这一性质来排除总体分布未知的障碍的。当然，也有一些非参数方法并不涉及秩的性质。

结(ties)的处理:
很多情况下，数据中会出现相同的观测值，那么对它们进行排序后，这些相同观测值的排名显然是并列的，也就是说它们的秩是相等的，这种情况被称为数据中的“结”
对于结的处理，通常是以它们排序后所处位置的平均值作为它们共同的秩
当一个数据中结比较多时，某些非参数检验中原假设下检验统计量的分布就会受到影响，从而需要对统计量进行修正(一般情况下，软件会自动作出修正)

Wilcoxon符号秩检验（Wilcoxon signed ranks test）是由Frank Wilcoxon于1945年提出的，它是单样本t检验的一种替代方法，用于检验总体中位数是否等于某个假设的值。该检验假定样本数据来自连续对称分布的总体。设总体真实中位数为M，假设的中位数为M0， Wilcoxon符号秩检验的步骤如下：
第1步：提出假设
双侧检验：H0：M=M0，H1：M≠M0；
左侧检验：H0：M=M0，H1：M<M0；
右侧检验：H0：M=M0，H1：M>M0。

例题：
(数据: example6_4.RData) 沿用例6-4。假定样本数据来自连续对称分布总体，但不知道总体的具体分布。检验该企业生产的砖的厚度中位数是否等于5cm( 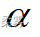=0.05)

注：函数 wilcox.test（x，…）中，参数m为假定的中位数，alternative=c(“two.side””less”，" greater"）指定备择假设的方向，默认为alternative="two.side”

load("C:/example/ch6/example6_4.RData")
wilcox.test(example6_4$厚度,m = 5)

注：函数 wilcox.test（x，…）中，参数m为假定的中位数，alternative=c(“two.side””less”，" greater"）指定备择假设的方向，默认为alternative="two.side”
结论：在该项检验中，统计量V=2，P=0.0005812，由于P<0.05，拒绝H0。有证据显示该企业生产的砖的厚度中位数与5cm有显著差异。

---

练习

1、(数据: exercise6_2.RData) 安装于一种联合收割机的金属板的平均重量为25千克。对某企业生产的20块全属板进行测量，得到的重量数据如下：
（1）采用 Shapiro-Wik检验方法，检验该企业生产的全属板的重量是否从正态分布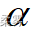（ =0.05）

解：提出假设：
H0:该企业生产的全属板的重量服从正态分布；H1:该企业生产的全属板的重量不服从正态分布

load("C:/example/ch6/exercise6_2.RData")
shapiro.test(exercise6_2$重量)

结论：在该项检验中，W=0.97064，P=0.7684，由于P>0.05，不拒绝原假设，没有证据显示该企业生产的金属板的重量不服从正态分布。

（2）假定金属板的重量服从正态分布，检验该企业生产的金属板是否符合要求 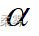（ =0.05）
解：提出假设：该企业生产的全属板的平均重量为μ
H0: μ=25；H1:μ 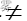25

t.test(exercise6_2$重量,mu=25,conf.level=0.95)

结论：P=0.3114>0.05,不拒绝原假设，没有证据表明该企业生产的金属板的重量不符合要求。

（3）计算效应量，分析差异程度
单样本t检验的效应量：
library(lsr)
cohensD(exercise6_2$重量,mu=25)

结论：0.2<d<0.5 小的效应量