Task04：DDPG、TD3算法

本篇博客是本人参加Datawhale组队学习第四次任务的笔记
【教程地址】https://github.com/datawhalechina/joyrl-book
【强化学习库JoyRL】https://github.com/datawhalechina/joyrl/tree/main
【JoyRL开发周报】 https://datawhale.feishu.cn/docx/OM8fdsNl0o5omoxB5nXcyzsInGe?from=from_copylink
【教程参考地址】https://github.com/datawhalechina/easy-rl

文章目录

DDPG算法
- DPG 方法
- DDPG 算法
- DDPG 算法的优缺点
TD3 算法
- 双Q网络
- 延迟更新
- 躁声正则
实战
- 实战：DDPG算法
- - 伪代码
  - 定义算法
  - 定义经验回放
  - DDPG_HER算法
  - 模型训练与测试
  - 定义环境
  - 可视化训练
- 实战：TD3 算法
练习
总结

DDPG算法

深度确定性策略梯度算法(deep deterministic policy gradient，DDPG)

初衷其实是DQN算法的一个连续动作空间版本扩展
DDPG算法的时候发现其在形式上更像Actor-Critic的架构

DPG 方法

将选择动作的过程变成一个直接从状态映射到具体动作的函数 $\mu_\theta (s)$
算法并没有做真正意义上的梯度更新，只是在寻找最大值，本质上还是DQN算法的思路

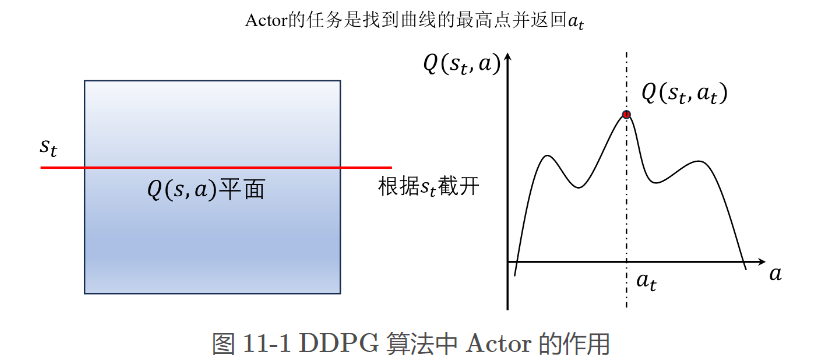
DDPG算法中Critic结构会同时包含状态和动作输入，而不是Actor-Critic算法中那样只包含状态
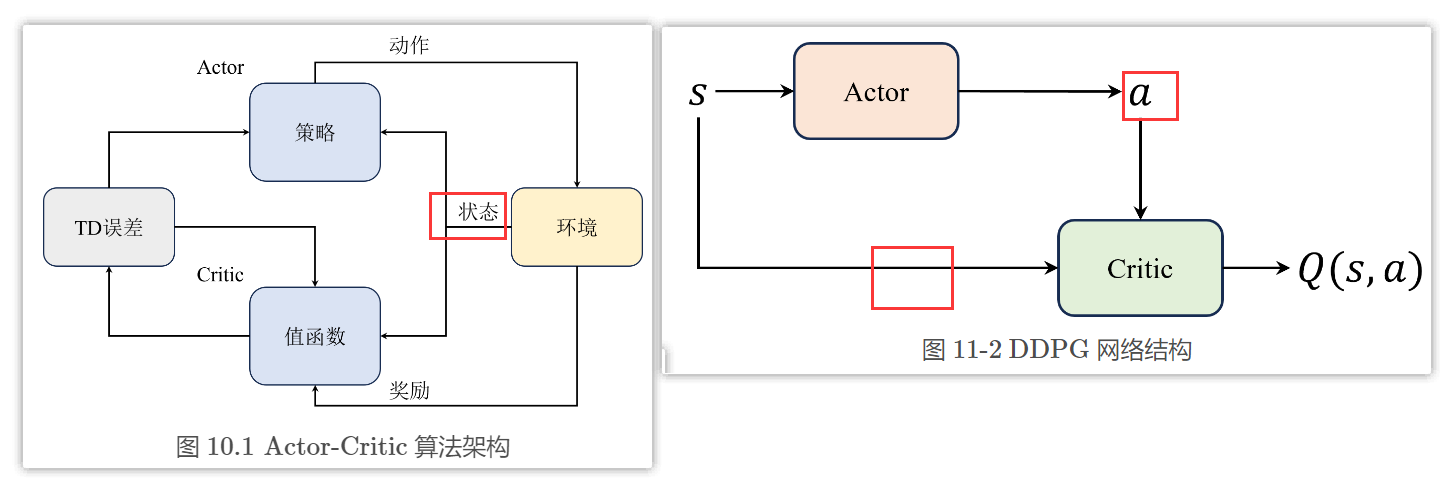
在这里插入图片描述

这里相当于是把 $\text{DQN}$ 算法中 $\varepsilon-\text{greedy}$ 策略函数部分换成了 $\text{Actor}$
这里的 $\mu_\theta (s)$ 输出的是一个动作值，而不是像 $\text{Actor-Critic}$ 章节中提到的概率分布 $\pi_{\theta}(a|s)$ 。
$Q(s_t, a)$ 相当于一个Critic网络，将状态和动作作为输入，并且输出一个值

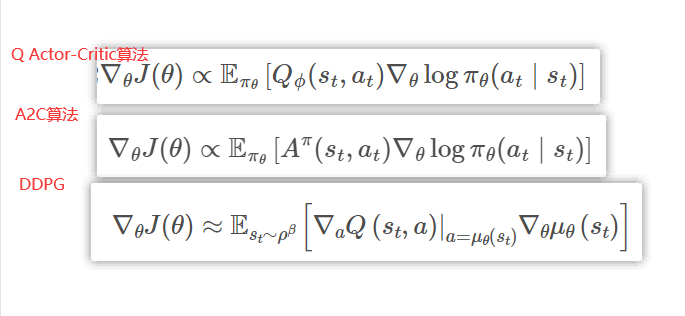
在这里插入图片描述

DDPG 算法

强化学习的关键问题：

如何提高对值函数的估计
如何提高探索以及平衡探索-利用的问题

引入噪声的作用就是为了在不破坏系统的前提下，提高系统运行的抗干扰性，实际上是在解决探索的问题。

DDPG与Noisy DQN中噪声的区别：

Noisy DQN在网络层中引入噪声
DDPG在动作中引入噪声

那DDPG中引入的是什么噪声呢？DDPG使用的其实是一种叫做 $\text{Ornstein-Uhlenbeck}$ 的噪声，简称 $\text{OU}$ 噪声。 $\text{OU}$ 噪声是一种具有回归特性的随机过程，其与高斯噪声相比的优点在于：

探索性： $\text{OU}$ 噪声具有持续的、自相关的特性。相比于独立的高斯噪声， $\text{OU}$ 噪声更加平滑，并且在训练过程中更加稳定。这种平滑特性使得OU噪声有助于探索更广泛的动作空间，并且更容易找到更好的策略。
控制幅度： $\text{OU}$ 噪声可以通过调整其参数来控制噪声的幅度。在 $\text{DDPG}$ 算法中，可以通过调整 $\text{OU}$ 噪声的方差来控制噪声的大小，从而平衡探索性和利用性。较大的方差会增加探索性，而较小的方差会增加利用性。
稳定性： $\text{OU}$ 噪声的回归特性使得噪声在训练过程中具有一定的稳定性。相比于纯粹的随机噪声，在 $\text{DDPG}$ 算法中使用 $\text{OU}$ 噪声可以更好地保持动作的连续性，避免剧烈的抖动，从而使得训练过程更加平滑和稳定。
可控性：由于 $\text{OU}$ 噪声具有回归特性，它在训练过程中逐渐回归到均值，因此可以控制策略的探索性逐渐减小。这种可控性使得在训练的早期增加探索性，然后逐渐减小探索性，有助于更有效地进行训练。

在简单的环境中，它跟使用简单的高斯噪声甚至不用噪声的效果是差不多的，只有在复杂的环境中才会体现出来区别，可以灵活选择噪声。

$\text{OU}$ 噪声主要由两个部分组成：随机高斯噪声和回归项，其数学定义如式如下：

$x_t=\theta\left(\mu-x_t\right) d t+\sigma d W_t$

$\qquad$ 其中 $x_t$ 是 $\text{OU}$ 过程在时间 $t$ 的值，即当前的噪声值，这个 $t$ 也是强化学习中的时步（ $\text{time step}$ ）。 $\mu$ 是回归到的均值，表示噪声在长时间尺度上的平均值。 $\theta$ 是 $\text{OU}$ 过程的回归速率，表示噪声向均值回归的速率。 $\sigma$ 是 $\text{OU}$ 过程的扰动项，表示随机高斯噪声的标准差。 $dW_t$ 是布朗运动（ $\text{Brownian motion}$ ）或者维纳过程（ $\text{Wiener process}$ ），是一个随机项，表示随机高斯噪声的微小变化。

DDPG 算法的优缺点

算法的优点主要有：
- 缓解了连续动作空间中的高方差问题
- 高效的梯度优化
- 经验回放和目标网络
缺点：
- 只适用于连续动作空间
- 高度依赖超参数
- 高度敏感的初始条件
- 由于采用了确定性策略，容易陷入局部最优

TD3 算法

TD3算法，英文全称为twin delayed DDPG，中文全称为双延迟确定性策略梯度算法。
相比于DDPG算法的改进：

双 $Q$ 网络，体现在名字中的 $\text{twin}$
延迟更新，体现在名字中的 $\text{delayed}$
躁声正则（ $\text{noise regularisation}$ ）

双Q网络

思想：在DDPC算法中的Critic网络上再加一层，这样就形成了两个Critic网络

DQN算法的过估计主要来源于两个方面：自举 (Bootstrap)和最大化，DDPG算法也是如此
- 如果Bootstrap是均匀的，对于智能体最终的决策不会带来影响；如果是非均匀的，对于智能体最终的决策会带来显著影响。然而实际上网络的Bootstrap通常是非均匀的。
- 最大化操作会使得网络的估计值大于真实值，从而造成网络过估计

双重网络是解决最大化问题的有效方法。在TD3算法中，作者引入了两套相同网络架构的Critic网络。计算目标值时，会利用二者间的较小值来估计下一个状态动作对的状态动作价值，从而可以有效避免最大化问题带来的高估。
在这里插入图片描述

延迟更新

这里的延迟更新指的是Actor网络的延迟更新，即Critic网络更新多次之后再对Actor网络进行更新。这个想法其实是非常直观的，因为Actor网络是通过最大化累积期望回报来更新的，它需要利用Critic网络来进行评估。如果Critic网络非常不稳定，那么Actor网络自然也会出现震荡。

因此，我们可以让Critic网络的更新频率高于Actor网络，即等待Critic网络更加稳定之后再来帮助Actor网络更新。在实践中，Actor的更新频率一般要比Critic的更新频率低一个数量级，例如Critic每更新10次，Actor只更新1次。

Critic就好比领导，Actor则好比员工，领导不断给员工下达目标，员工不断地去完成目标，如果领导的决策经常失误，那么员工就很容易像无头苍蝇一样不知道该完成哪些目标.
因此，一个好的解决方式就是让领导学得比员工更快，领导学得更快了之后下达目标的失误率就会更低，这样员工就能够更好地完成目标了，从而提高整个团队的效率。

躁声正则

延迟更新只是让Critic带来的误差不要过分地影响到了Actor，而没有考虑改进Critic本身的稳定性。当更新Critic网络时，使用确定性策略的学习目标极易受到函数逼近误差的影响，从而导致目标估计的方差大，估计值不准确。这种诱导方差可以通过正则化来减少，因此作者模仿SARSA的学习更新，引入了一种深度价值学习的正则化策略——目标策略平滑。

这种方法主要强调：类似的行动应该具有类似的价值，这里的噪声是在Critic网络上引入的，而不是在输出动作上引入的，因此它跟DDPG算法中的噪声是不一样的

具体的实现:

利用目标动作周围的区域来计算目标值，从而有利于平滑估计值
在实际操作时，我们可以通过向目标动作中添加少量随机噪声，并在小批量中求平均值，来近似动作的期望。
添加的噪声是服从正态分布的，并且对采样的噪声做了裁剪，以保持目标接近原始动作

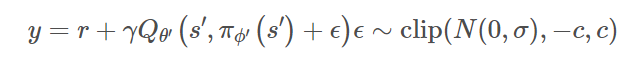
实战

实战：DDPG算法

伪代码

注意在第15步中 DDPG算法将当前网络参数复制到目标网络的方式是软更新，即每次一点点地将参数复制到目标网络中，与之对应的是DQN算法中的硬更新。软更新的好处是更加平滑缓慢，可以避免因权重更新过于迅速而导致的震荡，同时降低训练发散的风险。
在这里插入图片描述

定义算法

建立Actor网络、Critic网络和OU噪声类

class Actor(nn.Module):
    def __init__(self, n_states, n_actions, hidden_dim, init_w=3e-3):
        '''
        actor 模型的结构定义
        Args:
            n_states (int): 输入状态的维度
            n_actions (int): 可执行动作的数量
            hidden_dim (int): 隐含层数量
            init_w (float, optional): 均匀分布初始化权重的范围
        '''
        super(Actor, self).__init__()
        self.linear1 = nn.Linear(n_states, hidden_dim)
        self.linear2 = nn.Linear(hidden_dim, hidden_dim)
        self.linear3 = nn.Linear(hidden_dim, n_actions)

        self.linear3.weight.data.uniform_(-init_w, init_w)
        self.linear3.bias.data.uniform_(-init_w, init_w)

    def forward(self, x):
        x = F.relu(self.linear1(x))
        x = F.relu(self.linear2(x))
        x = torch.tanh(self.linear3(x))
        return x


class Critic(nn.Module):
    def __init__(self, n_states, n_actions, hidden_dim, init_w=3e-3):
        '''
        critic 模型的结构定义
        Args:
            n_states (int): 输入状态的维度
            n_actions (int): 可执行动作的数量
            hidden_dim (int): 隐含层数量
            init_w (float, optional): 均匀分布初始化权重的范围
        '''
        super(Critic, self).__init__()

        self.linear1 = nn.Linear(n_states + n_actions, hidden_dim)
        self.linear2 = nn.Linear(hidden_dim, hidden_dim)
        self.linear3 = nn.Linear(hidden_dim, 1)
        # 随机初始化为较小的值
        self.linear3.weight.data.uniform_(-init_w, init_w)
        self.linear3.bias.data.uniform_(-init_w, init_w)

    def forward(self, state, action):
        # 按维数1拼接
        x = torch.cat([state, action], 1)
        x = F.relu(self.linear1(x))
        x = F.relu(self.linear2(x))
        x = self.linear3(x)
        return x


class OUNoise(object):
    '''
    构造 Ornstein–Uhlenbeck 噪声的类
    '''

    def __init__(self, action_space, mu=0.0, theta=0.15, max_sigma=0.3, min_sigma=0.3, decay_period=100000):
        '''
        初始化输入参数
        Args:
            action_space (Union[gym.spaces.box.Box, gym.spaces.discrete.Discrete]): env 中的 action_space
            mu (float, optional): 噪声均值
            theta (float, optional): 系统对噪声的扰动程度，theta 越大，噪声扰动越小
            max_sigma (float, optional): 最大 sigma，用于更新衰变 sigma 值
            min_sigma (float, optional): 最小 sigma，用于更新衰变 sigma 值
            decay_period (int, optional): 衰变周期
        '''
        self.mu = mu
        self.theta = theta
        self.sigma = max_sigma
        self.max_sigma = max_sigma
        self.min_sigma = min_sigma
        self.decay_period = decay_period
        self.n_actions = action_space.shape[0]  # env环境中可执行动作的数量
        self.low = action_space.low  # env环境中动作取值的最小值
        self.high = action_space.high  # env环境中动作取值的最大值
        self.reset()

    def reset(self):
        '''
        重置噪声
        '''
        self.obs = np.ones(self.n_actions) * self.mu  # reset the noise

    def evolve_obs(self):
        '''
        更新噪声
        Returns:
            返回更新后的噪声值
        '''
        x = self.obs
        dx = self.theta * (self.mu - x) + self.sigma * np.random.randn(self.n_actions)  # Ornstein–Uhlenbeck process
        self.obs = x + dx
        return self.obs

    def get_action(self, action, t=0):
        '''
        根据输入的动作，输出加入 OU 噪声后的动作
        Args:
            action (array): 输入的动作值
            t (int, optional): 当前环境已执行的帧数

        Returns:
            action (float): 返回加入 OU 噪声后的动作
        '''
        ou_obs = self.evolve_obs()
        ## 根据env进程（t），通过设定的衰变周期（decay_period），进行更新衰变的sigma值
        self.sigma = self.max_sigma - (self.max_sigma - self.min_sigma) * min(1.0, t / self.decay_period)
        return np.clip(action + ou_obs, self.low, self.high)  # add noise to action

定义经验回放

class ReplayBufferQue:
    def __init__(self, capacity: int) -> None:
        self.capacity = capacity
        self.buffer = deque(maxlen=self.capacity)
    def push(self,transitions):
        '''_summary_
        Args:
            trainsitions (tuple): _description_
        '''
        self.buffer.append(transitions)
    def sample(self, batch_size: int, sequential: bool = False):
        if batch_size > len(self.buffer):
            batch_size = len(self.buffer)
        if sequential: # sequential sampling
            rand = random.randint(0, len(self.buffer) - batch_size)
            batch = [self.buffer[i] for i in range(rand, rand + batch_size)]
            return zip(*batch)
        else:
            batch = random.sample(self.buffer, batch_size)
            return zip(*batch)
    def clear(self):
        self.buffer.clear()
    def __len__(self):
        return len(self.buffer)

DDPG_HER算法

class DDPG_HER:
    def __init__(self, cfg):
        '''
        构建智能体
        Args:
            cfg (class): 超参数类 AlgoConfig
        '''
        self.n_states = cfg.n_states
        self.n_actions = cfg.n_actions
        self.states_dim = cfg.n_states * 2
        self.actions_dim = cfg.n_actions
        self.action_space = cfg.action_space  # env 中的 action_space
        self.ou_noise = OUNoise(self.action_space)  # 实例化 构造 Ornstein–Uhlenbeck 噪声的类
        self.batch_size = cfg.batch_size
        self.gamma = cfg.gamma
        self.tau = cfg.tau
        self.sample_count = 0  # 记录采样动作的次数
        self.update_flag = False  # 标记是否更新网络
        self.device = torch.device(cfg.device)
        self.critic = Critic(self.states_dim, self.actions_dim, hidden_dim=cfg.critic_hidden_dim).to(self.device)
        self.target_critic = Critic(self.states_dim, self.actions_dim, hidden_dim=cfg.critic_hidden_dim).to(self.device)
        self.actor = Actor(self.states_dim, self.actions_dim, hidden_dim=cfg.actor_hidden_dim).to(self.device)
        self.target_actor = Actor(self.states_dim, self    .actions_dim, hidden_dim=cfg.actor_hidden_dim).to(self.device).to(
            self.device)
        ## 将 critc 网络的参数赋值给target critic 网络
        for target_param, param in zip(self.target_critic.parameters(), self.critic.parameters()):
            target_param.data.copy_(param.data)
        ## 将 actor 网络的参数赋值给target actor 网络
        for target_param, param in zip(self.target_actor.parameters(), self.actor.parameters()):
            target_param.data.copy_(param.data)
        self.critic_optimizer = optim.Adam(self.critic.parameters(), lr=cfg.critic_lr)
        self.actor_optimizer = optim.Adam(self.actor.parameters(), lr=cfg.actor_lr)
        self.memory = ReplayBufferQue(cfg.buffer_size)

    def sample_action(self, state):
        '''
        根据输入的状态采样动作
        Args:
            state (array): 输入的状态

        Returns:
            action (float): 根据状态采样后的动作
        '''
        self.sample_count += 1
        state = torch.tensor(state, device=self.device, dtype=torch.float32).unsqueeze(dim=0)
        action_tanh = self.actor(state)  # action_tanh is in [-1, 1]
        # convert action_tanh to action in the original action space
        action_scale = torch.FloatTensor((self.action_space.high - self.action_space.low) / 2.).to(self.device)
        action_bias = torch.FloatTensor((self.action_space.high + self.action_space.low) / 2.).to(self.device)
        action = action_scale * action_tanh + action_bias
        action = action.cpu().detach().numpy()[0]
        # add noise to action
        action = self.ou_noise.get_action(action, self.sample_count)
        return action

    @torch.no_grad()
    def predict_action(self, state):
        '''
        根据输入的状态预测下一步的动作
        Args:
            state (array):  输入的状态

        Returns:
            action (float): 根据状态采样后的动作
        '''
        state = torch.tensor(state, device=self.device, dtype=torch.float32).unsqueeze(dim=0)
        action_tanh = self.actor(state)  # action_tanh is in [-1, 1]
        # convert action_tanh to action in the original action space
        action_scale = torch.FloatTensor((self.action_space.high - self.action_space.low) / 2.).to(self.device)
        action_bias = torch.FloatTensor((self.action_space.high + self.action_space.low) / 2.).to(self.device)
        action = action_scale * action_tanh + action_bias
        action = action.cpu().detach().numpy()[0]
        return action

    def update(self):
        ## 当经验回放池中的数量小于 batch_size 时，直接返回不更新
        if len(self.memory) < self.batch_size:  # when memory size is less than batch size, return
            return
        else:
            if not self.update_flag:
                print("Begin to update!")
                self.update_flag = True
        ## 从经验回放池中采样 batch_size 个样本
        state, action, reward, next_state, done = self.memory.sample(self.batch_size)
        ## 将状态、动作等 array 转为 tensor
        state = torch.FloatTensor(np.array(state)).to(self.device)
        next_state = torch.FloatTensor(np.array(next_state)).to(self.device)
        action = torch.FloatTensor(np.array(action)).to(self.device)
        reward = torch.FloatTensor(reward).unsqueeze(1).to(self.device)
        done = torch.FloatTensor(np.float32(done)).unsqueeze(1).to(self.device)
        ## 输入状态及通过 actor 网络 根据该状态输出的动作，计算 critic 网络输出的价值，类似于DQN中的q-value
        policy_loss = self.critic(state, self.actor(state))
        ## 计算均值作为 critic 网络的损失
        policy_loss = -policy_loss.mean()
        ## 根据下一个 timestamp 的状态用 target_actor 网络输出目标动作
        next_action = self.target_actor(next_state)
        ## 输入下一个 timestamp 的状态及目标动作，计算 target_critc 网络输出的目标价值
        target_value = self.target_critic(next_state, next_action.detach())
        ## 根据真实奖励更新目标价值
        expected_value = reward + (1.0 - done) * self.gamma * target_value
        expected_value = torch.clamp(expected_value, -np.inf, np.inf)
        ## 输入状态和动作，用 critic 网络计算预估的价值
        value = self.critic(state, action)
        ## 将 critic 网络输出的价值和 target_critic输出并更新后的价值通过MSE进行损失计算
        value_loss = nn.MSELoss()(value, expected_value.detach())
        ## 更新 actor 网络参数
        self.actor_optimizer.zero_grad()
        policy_loss.backward()
        self.actor_optimizer.step()
        ## 更新 critic 网络参数
        self.critic_optimizer.zero_grad()
        value_loss.backward()
        self.critic_optimizer.step()
        ## 通过软更新的方法，缓慢更新 target critic 网络的参数
        for target_param, param in zip(self.target_critic.parameters(), self.critic.parameters()):
            target_param.data.copy_(
                target_param.data * (1.0 - self.tau) +
                param.data * self.tau
            )
        ## 通过软更新的方法，缓慢更新 target actor 网络的参数
        for target_param, param in zip(self.target_actor.parameters(), self.actor.parameters()):
            target_param.data.copy_(
                target_param.data * (1.0 - self.tau) +
                param.data * self.tau
            )

    def save_model(self, fpath):
        '''
        保存模型
        Args:
            fpath (str): 模型存放路径
        '''
        from pathlib import Path
        # create path

        Path(fpath).mkdir(parents=True, exist_ok=True)
        torch.save(self.actor.state_dict(), f"{fpath}/actor_checkpoint.pt")

    def load_model(self, fpath):
        '''
        根据模型路径导入模型
        Args:
            fpath (str): 模型路径
        '''
        actor_ckpt = torch.load(f"{fpath}/actor_checkpoint.pt", map_location=self.device)
        self.actor.load_state_dict(actor_ckpt)

模型训练与测试

定义奖励计算函数和目标生成函数

def calcu_reward(new_goal, state, action):
    # direcly use observation as goal
    goal_cos, goal_sin, goal_thdot = new_goal[0], new_goal[1], new_goal[2]
    cos_th, sin_th, thdot = state[0], state[1], state[2]
    costs = angle_normalize(np.arccos(goal_cos) - np.arccos(cos_th)) ** 2 + 0.1 * (goal_thdot - thdot) ** 2#+ (goal_sin - sin_th) ** 2 
    reward = -costs
    return reward

def generate_goals(i, episode_cache, sample_num, sample_range = 200):
    '''
    Input: current steps, current episode transition's cache, sample number
    Return: new goals sets
    notice here only "future" sample policy
    '''
    end = (i+sample_range) if i+sample_range < len(episode_cache) else len(episode_cache)
    epi_to_go = episode_cache[i:end]
    if len(epi_to_go) < sample_num:
        sample_trans = epi_to_go
    else:
        sample_trans = random.sample(epi_to_go, sample_num)
    return [np.array(trans[3][:3]) for trans in sample_trans]#episode_cache.append((o,a,r,o2))

def angle_normalize(x):
    return ((x + np.pi) % (2 * np.pi)) - np.pi

训练函数与测试函数

def train(cfg, env, agent):
    print("开始训练！")
    rewards = [] # 记录所有回合的奖励
    for i_ep in range(cfg.train_eps):
        ep_reward = 0  # reward per episode
        ep_step = 0
        episode_cache = []
        HER_SAMPLE_NUM = cfg.her_sample_num
        update_every = cfg.update_every
        state, _ = env.reset()  # 环境状态
        # 随机构造目标
        np.random.seed(cfg.seed)
        costheta = np.random.rand()
        sintheta = np.sqrt(1-costheta**2)
        w = 2 * np.random.rand()
        goal = np.array([costheta,sintheta,w])
        state = np.concatenate((state, goal)) # 结合环境状态和目标，构造新状态
        for _ in range(cfg.max_steps):
            ep_step += 1
            action = agent.sample_action(state)  # sample action
            next_state, reward, terminated, _, info = env.step(
                action)  # update env and return transitions under new_step_api of OpenAI Gym
            next_state = np.concatenate((next_state, goal)) # 结合下一时间步环境状态和目标，构造新下一时间步状态
            reward = calcu_reward(goal, state, action) # 根据目标、状态、动作计算HER奖励
            episode_cache.append((state, action, reward, next_state)) # 缓存transitions，便于事后经验回放
            agent.memory.push((state, action, reward,
                               next_state, terminated))  # 将transitions存入经验缓存池
            
            state = next_state  # update next state for env
            ep_reward += reward  #
            if terminated:
                break

        # Hindsight replay: Important operation of HER
        for i, transition in enumerate(episode_cache):
            new_goals = generate_goals(i, episode_cache, HER_SAMPLE_NUM) # 根据future方法构造新目标
            for new_goal in new_goals:
                state, action = transition[0], transition[1] # 从transition提取具有目标的状态和动作
                reward = calcu_reward(new_goal, state, action) # 根据新目标、状态、动作计算奖励值
            
                state, new_state = transition[0][:3], transition[3][:3] # 从transition提取不包含目标的状态和下一时间步状态
                state = np.concatenate((state, new_goal)) # 结合环境状态和生成的新目标，构造新状态
                new_state = np.concatenate((new_state, new_goal)) # 结合下一时间步环境状态和生成的新目标，构造新下一时间步状态
                agent.memory.push((state, action, reward, new_state, False)) # 将新的transition存入经验缓存池


        for _ in range(update_every):
            agent.update()  # update agent
        rewards.append(ep_reward)
    print("完成训练！")
    return {'rewards':rewards}
def test(cfg, env, agent):
    print("开始测试！")
    rewards = [] # 记录所有回合的奖励
    for i_ep in range(cfg.train_eps):
        ep_reward = 0  # reward per episode
        ep_step = 0
        ep_frames = []
        state, _ = env.reset(seed = cfg.seed)  # 环境状态
        # 随机构造目标
        costheta = np.random.rand()
        sintheta = np.sqrt(1-costheta**2)
        w = 2 * np.random.rand()
        goal = np.array([costheta,sintheta,w])
        state = np.concatenate((state, goal)) # 结合环境状态和目标，构造新状态
        for _ in range(cfg.max_steps):
            ep_step += 1
            if cfg.render and cfg.render_mode == 'rgb_array': # 用于可视化
                frame = env.render()[0]
                ep_frames.append(frame)
            action = agent.predict_action(state)  # sample action
            next_state, reward, terminated, _, info= env.step(
                action)  # update env and return transitions under new_step_api of OpenAI Gym
            next_state = np.concatenate((next_state, goal)) # 结合下一时间步环境状态和目标，构造新下一时间步状态
            state = next_state  # update next state for env
            ep_reward += reward
            if terminated:
                break
        rewards.append(ep_reward)
        print(f"回合：{i_ep+1}/{cfg.test_eps}，奖励：{ep_reward:.2f}")
    print("完成测试！")
    return {'rewards':rewards}

定义环境

import gymnasium as gym
import os
def all_seed(env,seed = 1):
    ''' 万能的seed函数
    '''
#     env.seed(seed) # env config
    np.random.seed(seed)
    random.seed(seed)
    torch.manual_seed(seed) # config for CPU
    torch.cuda.manual_seed(seed) # config for GPU
    os.environ['PYTHONHASHSEED'] = str(seed) # config for python scripts
    # config for cudnn
    torch.backends.cudnn.deterministic = True
    torch.backends.cudnn.benchmark = False
    torch.backends.cudnn.enabled = False
def env_agent_config(cfg):
    env = gym.make(cfg.env_name) # 创建环境
    all_seed(env,seed=cfg.seed)
    n_states = env.observation_space.shape[0]
    n_actions = env.action_space.shape[0]
    print(f"状态空间维度：{n_states}，动作空间维度：{n_actions}")
    # 更新n_states和n_actions到cfg参数中
    setattr(cfg, 'n_states', n_states)
    setattr(cfg, 'n_actions', n_actions) 
    setattr(cfg, 'action_space', env.action_space) 
    models = {"actor":Actor(n_states,n_actions,hidden_dim=cfg.actor_hidden_dim),"critic":Critic(n_states,n_actions,hidden_dim=cfg.critic_hidden_dim)}
    memory = ReplayBufferQue(cfg.buffer_size) # 创建经验池
    agent = DDPG_HER(cfg)
    return env,agent

可视化训练

import argparse
import matplotlib.pyplot as plt
import seaborn as sns
class Config:
    def __init__(self):
        self.algo_name = 'DDPG_HER' # 算法名称
        self.env_name = 'Pendulum-v1' # 环境名称
        self.new_step_api = True # whether to use new step api of gym
        self.wrapper = None # wrapper of environment
        self.render = False # whether to render environment
        self.render_mode = "human" # 渲染模式, "human" 或者 "rgb_array"
        self.mode = "train" # train or test
        self.mp_backend = "mp" # 多线程框架，ray或者mp(multiprocessing)，默认mp
        self.seed = 0 # random seed
        self.device = "cpu" # device to use
        self.train_eps = 150 # number of episodes for training
        self.test_eps = 20 # number of episodes for testing
        self.eval_eps = 10 # number of episodes for evaluation
        self.eval_per_episode = 5 # evaluation per episode
        self.max_steps = 200 # max steps for each episode
        self.gamma = 0.99  # 贴现因子，值越大，表示未来的收益占更大的比重
        self.critic_lr = 1e-3  # critic 模型的学习率
        self.actor_lr = 1e-3  # actor 模型的学习率
        self.buffer_size = 10000  # 经验回放池的大小
        self.batch_size = 128  # 训练 actor 及 critic 模型的 batch 大小
        self.tau = 0.01  # 软更新参数，值越小，表示在更新目标网络参数时，参数变化越小
        self.critic_hidden_dim = 256  # critic 网络的隐含层数
        self.actor_hidden_dim = 256  # actor 网络的隐含参数
        self.her_sample_num = 4 # her抽样数量
        self.update_every = 100 # 每代更新次数
def smooth(data, weight=0.9):  
    '''用于平滑曲线，类似于Tensorboard中的smooth曲线
    '''
    last = data[0] 
    smoothed = []
    for point in data:
        smoothed_val = last * weight + (1 - weight) * point  # 计算平滑值
        smoothed.append(smoothed_val)                    
        last = smoothed_val                                
    return smoothed

def plot_rewards(rewards,title="learning curve"):
    sns.set()
    plt.figure()  # 创建一个图形实例，方便同时多画几个图
    plt.title(f"{title}")
    plt.xlim(0, len(rewards), 10)  # 设置x轴的范围
    plt.xlabel('episodes')
    plt.plot(rewards, label='rewards')
    plt.plot(smooth(rewards), label='smoothed')
    plt.legend()

# 获取参数
cfg = Config() 
# 训练
env, agent = env_agent_config(cfg)
res_dic = train(cfg, env, agent)
 
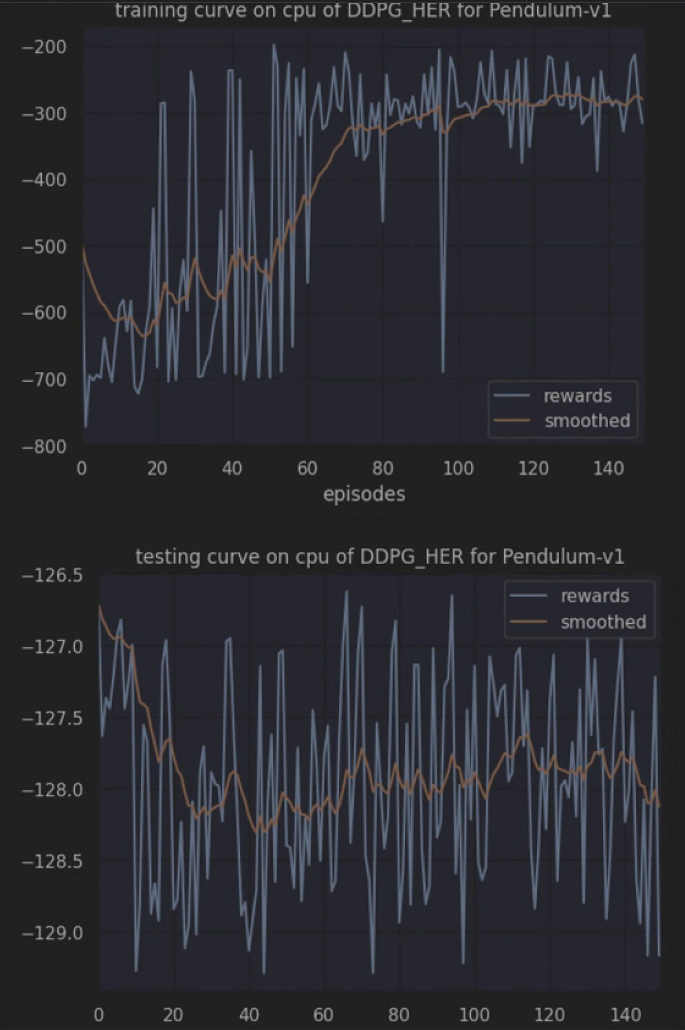
plot_rewards(res_dic['rewards'], title=f"training curve on {cfg.device} of {cfg.algo_name} for {cfg.env_name}")  
# 测试
res_dic = test(cfg, env, agent)
plot_rewards(res_dic['rewards'], title=f"testing curve on {cfg.device} of {cfg.algo_name} for {cfg.env_name}")  # 画出结果

在这里插入图片描述

实战：TD3 算法

TD3算法只是在策略更新上与DDPG算法有所差异，其它地方基本相同。

def update(self):
    if len(self.memory) < self.explore_steps: # 当经验回放中不满足一个批量时，不更新策略
        return
    state, action, reward, next_state, done = self.memory.sample(self.batch_size) # 从经验回放中随机采样一个批量的转移(transition)
           # 将数据转换为tensor
    state = torch.tensor(np.array(state), device=self.device, dtype=torch.float32)
    action = torch.tensor(np.array(action), device=self.device, dtype=torch.float32)
    next_state = torch.tensor(np.array(next_state), device=self.device, dtype=torch.float32)
    reward = torch.tensor(reward, device=self.device, dtype=torch.float32).unsqueeze(1)
    done = torch.tensor(done, device=self.device, dtype=torch.float32).unsqueeze(1)
    noise = (torch.randn_like(action) * self.policy_noise).clamp(-self.noise_clip, self.noise_clip) # 构造加入目标动作的噪声
          # 计算加入了噪声的目标动作
    next_action = (self.actor_target(next_state) + noise).clamp(-self.action_scale+self.action_bias, self.action_scale+self.action_bias)
          # 计算两个critic网络对t+1时刻的状态动作对的评分，并选取更小值来计算目标q值
    target_q1, target_q2 = self.critic_1_target(next_state, next_action).detach(), self.critic_2_target(next_state, next_action).detach()
    target_q = torch.min(target_q1, target_q2)
    target_q = reward + self.gamma * target_q * (1 - done)
          # 计算两个critic网络对t时刻的状态动作对的评分
    current_q1, current_q2 = self.critic_1(state, action), self.critic_2(state, action)
          # 计算均方根损失
    critic_1_loss = F.mse_loss(current_q1, target_q)
    critic_2_loss = F.mse_loss(current_q2, target_q)
    self.critic_1_optimizer.zero_grad()
    critic_1_loss.backward()
    self.critic_1_optimizer.step()
    self.critic_2_optimizer.zero_grad()
    critic_2_loss.backward()
    self.critic_2_optimizer.step()
    if self.sample_count % self.policy_freq == 0:
              # 延迟策略更新，actor的更新频率低于critic
        actor_loss = -self.critic_1(state, self.actor(state)).mean()
        self.actor_optimizer.zero_grad()
        actor_loss.backward()
        self.actor_optimizer.step()
              #目标网络软更新
        for param, target_param in zip(self.actor.parameters(), self.actor_target.parameters()):
            target_param.data.copy_(self.tau * param.data + (1 - self.tau) * target_param.data)
        for param, target_param in zip(self.critic_1.parameters(), self.critic_1_target.parameters()):
            target_param.data.copy_(self.tau * param.data + (1 - self.tau) * target_param.data)
        for param, target_param in zip(self.critic_2.parameters(), self.critic_2_target.parameters()):
            target_param.data.copy_(self.tau * param.data + (1 - self.tau) * target_param.data)

练习

$\text{DDPG}$ 算法是 $\text{off-policy}$ 算法吗？为什么？

跟 $\text{DQN}$ 一样， $\text{DDPG}$ 算法，主要结合了经验回放、目标网络和确定性策略，是典型的
$\text{off-policy}$ 算法。
强化学习中的奇怪概念(一)——On-policy与off-policy

软更新相比于硬更新的好处是什么？为什么不是所有的算法都用软更新？

好处：
平滑目标更新：软更新通过逐渐调整目标网络的参数，使其向主网络的参数靠近，而不是直接复制主网络的参数。这样做可以降低目标的变化幅度，减少了训练中的不稳定性；
降低方差；
避免振荡：软更新可以减少目标网络和主网络之间的振荡，这有助于更稳定地收敛到良好的策略。

缺点：
速度：软更新会使目标网络变得更加缓慢；
探索和稳定性权衡：一些算法可能更倾向于使用硬更新，因为它们可能需要更频繁地探索新的策略，而不依赖于过去的经验。硬更新允许在每次更新时完全用新策略替代旧策略；
算法需求：某些算法可能对硬更新更敏感，而且硬更新可能是这些算法的关键组成部分。综上，软更新和硬更新都有其用途，选择哪种方式取决于具体的问题和算法要求。

相比于 $\text{DDPG}$ 算法， $\text{TD3}$ 算法做了哪些改进？请简要归纳。

双Q网络： $\text{TD3}$ 使用了两个独立的 $\text{Q}$ 网络，分别用于估计动作的价值。这两个Q网络有不同的参数，这有助于减少估计误差，并提高了训练的稳定性；
目标策略噪声：与 $\text{DDPG}$ 不同， $\text{TD3}$ 将噪声添加到目标策略，而不是主策略。这有助于减小动作值的过估计误差；
目标策略平滑化： $\text{TD3}$ 使用目标策略平滑化技术，通过对目标策略的参数进行软更新来减小目标策略的变化幅度。这有助于提高稳定性和训练的收敛性。
延迟策略更新： $\text{TD3}$ 引入了延迟策略更新，意味着每隔一定数量的时间步才更新主策略网络。这可以减小策略更新的频率，有助于减少过度优化的风险，提高稳定性。

$\text{TD3}$ 算法中 $\text{Critic}$ 的更新频率一般要比 $\text{Actor}$ 是更快还是更慢？为什么？

$\text{Critic}$ 网络的更新频率要比 $\text{Actor}$
网络更快，即延迟策略更新。延迟策略更新的目的是减小策略更新的频率，以避免过度优化和提高训练的稳定性。因为 $\text{Critic}$
网络的更新频率更高，它可以更快地适应环境的变化，提供更准确的动作价值估计，从而帮助 $\text{Actor}$ 网络生成更好的策略。

总结

本文主要介绍了强化学习中较为常用的一类算法，即 DDPG和TD3算法，它们虽然在结构上被归类于Actor-Critic算法，但从原理上来说跟DQN算法更为接近。先介绍了DDPG算法，它相当于DQN算法的一个连续动作空间版本扩展，它在DDPG在动作中引入噪声进一步提升了模型的探索能力。
之后介绍了TD3算法，它主要包括了双Q网络、延迟更新和躁声正则。最后进行了代码实战。