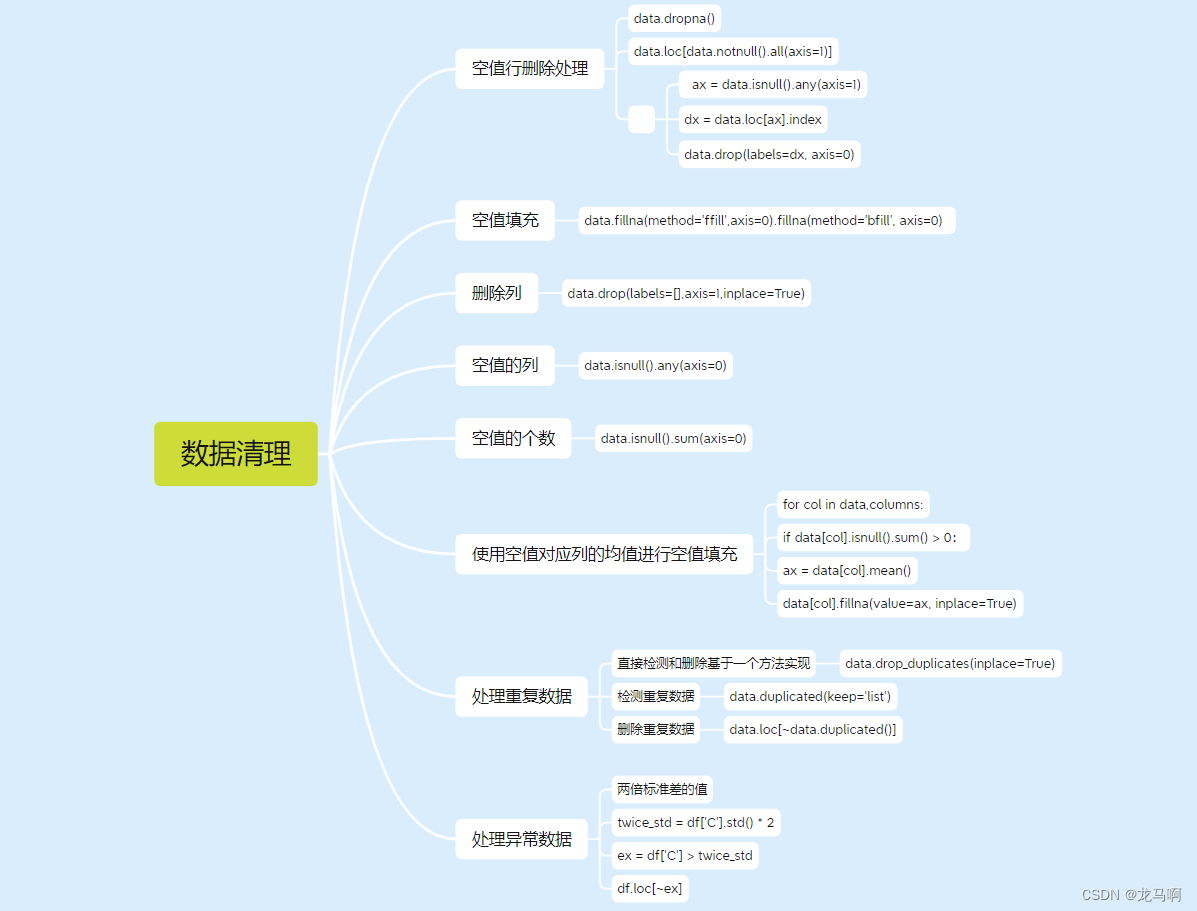
数据处理

1. 去除重复数据

# 删除重复值 保留重复行 第一行的数据
data.drop_duplicates(inplace=True, keep='first')

2. 数据格式转化

日期格式化

data['order_date'] = pd.to_datetime(data['order_dt'], format='%Y%m%d')

data['销售时间'] = pd.to_datetime(data['销售时间']) # 交货时间  销售时间
data['月份'] = data['销售时间'].map(lambda x: x.month)

# dir = {'1': '一季度', '2': '一季度', '3': '一季度', '4': '二季度', '5': '二季度', '6': '二季度', '7': '三季度', '8': '三季度', '9': '三季度', '10': '四季度', '11': '四季度', '12': '四季度'}
# data['季度'] = data['月份'].map(lambda x: str(x)).map(lambda x: dir[x])
# data.groupby(by='季度')['货品'].count().plot.bar()

# 将 order_date 转成 精度是 月份的数据列
data_text['order_date_month'] = data_text['order_date'].values.astype('datetime64[M]')

去除前后空格

# 去除前后空格
data['货品交货状况'] = data['货品交货状况'].str.strip()

3. 删除空值行

# 第一部分
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
plt.rcParams['font.sans-serif'] = 'SimHei' ## 设置中文显示
%matplotlib inline 
route = 'meal_order_detail.xlsx'
data1 = pd.read_excel(route, sheet_name='meal_order_detail1')
data2 = pd.read_excel(route, sheet_name='meal_order_detail2')
data3= pd.read_excel(route, sheet_name='meal_order_detail3')
data = pd.concat([data1, data2,data3],axis=0)
data.head(5)

# 第二部分  清除 Na 的值 删除空值行
data.dropna(axis=1, inplace=True)

4. 删除指定列，或者空值列

# 删除订单这一列数据
data.drop(columns=['订单行'], inplace=True, axis=1)

# 删除空值列 axis=0
data.dropna(axis=0, inplace=True, how='any | all')

5. 异常数据处理

取出 索引值 1 2 3 , 列名 'A' 'B'
data.loc[[1,2,3] , ['A','B']]

异常值处理原则  数值分布在（μ-3σ,μ+3σ)中的概率为0.9973
最小值
平均数 - 3*标准差
最大值
平均数 + 3*标准差

# 第一部分
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
plt.rcParams['font.sans-serif'] = 'SimHei' ## 设置中文显示
%matplotlib inline 
route = 'meal_order_detail.xlsx'
data1 = pd.read_excel(route, sheet_name='meal_order_detail1')
data2 = pd.read_excel(route, sheet_name='meal_order_detail2')
data3= pd.read_excel(route, sheet_name='meal_order_detail3')
data = pd.concat([data1, data2,data3],axis=0)


def three_sigma(ser):
    """
    自实现3sigma 原则
    :param ser: 数据
    :return: 处理完成的数据
    """
    bool_id = ((ser.mean() - 3 * ser.std()) <= ser)  &   (ser <= (ser.mean() + 3 * ser.std()))
    # bool_id 数组索引
    # ser[bool_id]
    return ser.index[bool_id]
# 调用3sigma原则，进行异常值过滤
index_name_list = three_sigma(data['amounts'])
deatil = data.loc[index_name_list,:]

6. 空值填充

# 相邻前面的值或者后面的值填充
data.fillna(method='ffill',axis=0).fillna(method='bfill', axis=0)

# 使用空值对应列的均值进行空值填充
for col in data,columns:
	if data[col].isnull().sum() > 0：
	ax = data[col].mean()
	data[col].fillna(value=ax, inplace=True)