今日任务
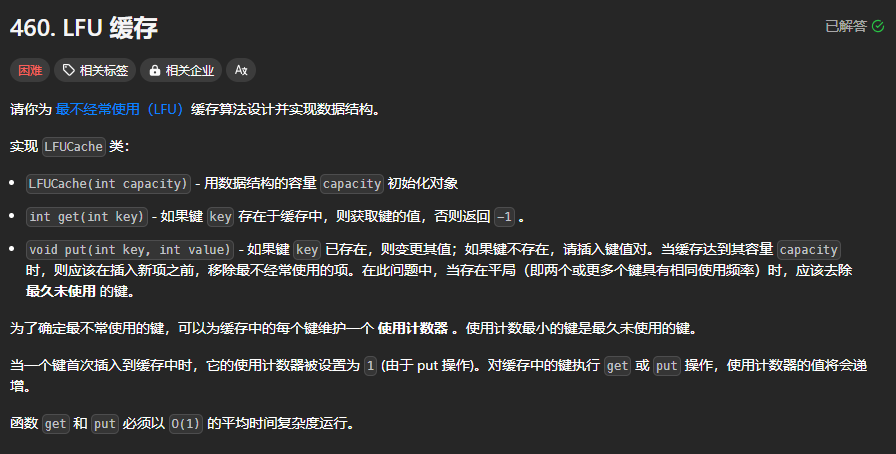
- 332.重新安排行程
- 51. N皇后
- 37. 解数独
- 总结
总结
回溯总结:代码随想录
回溯是递归的副产品,只要有递归就会有回溯,所以回溯法也经常和二叉树遍历,深度优先搜索混在一起,因为这两种方式都是用了递归。
回溯法就是暴力搜索,并不是什么高效的算法,最多再剪枝一下。
回溯法的模板:for循环横向遍历,递归纵向遍历,回溯不断调整结果集
void backtracking(参数) { if (终止条件) { 存放结果; return; } for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) { 处理节点; backtracking(路径,选择列表); // 递归 回溯,撤销处理结果 } }回溯算法能解决如下问题:
组合问题:N个数里面按一定规则找出k个数的集合
组合:用递归控制for循环嵌套的数量;优化回溯算法只有剪枝一种方法,for循环在寻找起点的时候要有一个范围,如果这个起点到集合终止之间的元素已经不够题目要求的k个元素了,就没有必要搜索了
组合总和:已选元素总和如果已经大于n(题中要求的和)了,那么往后遍历就没有意义了,直接剪掉
组合总和(可重复元素):需要startIndex来控制for循环的起始位置,如果是一个集合来求组合的话,就需要startIndex;如果是多个集合取组合,各个集合之间相互不影响,那么就不用startIndex
组合总和(元素重复,答复不重复):难在去重,“树枝去重”和“树层去重”
多个集合求组合:还是熟悉的模板题目,但是有一些细节
排列问题:N个数按一定规则全排列,有几种排列方式
排列:每层都是从0开始搜索而不是startIndex,需要used数组记录path里都放了哪些元素了
去重排列:神奇的地方就是used[i - 1] == false也可以,used[i - 1] == true也可以;使用(used[i - 1] == false),即树层去重,效率更高;used数组既是记录path里都放了哪些元素,同时也用来去重,一举两得。
切割问题:一个字符串按一定规则有几种切割方式
切割问题其实类似组合问题
如何模拟那些切割线
切割问题中递归如何终止
在递归循环中如何截取子串
如何判断回文
子集问题:一个N个数的集合里有多少符合条件的子集
子集:在树形结构中,要收集所有节点的结果
去重子集:去重套路
递增子序列:使用set针对同一父节点本层去重
棋盘问题:N皇后,解数独等等去重:
使用set去重的版本相对于used数组的版本效率都要低很多:主要是因为程序运行的时候对unordered_set 频繁的insert,unordered_set需要做哈希映射(也就是把key通过hash function映射为唯一的哈希值)相对费时间,而且insert的时候其底层的符号表也要做相应的扩充,也是费时的。使用used数组在时间复杂度上几乎没有额外负担
使用set去重,不仅时间复杂度高了,空间复杂度也高了:组合,子集,排列问题的空间复杂度都是O(n),但如果使用set去重,空间复杂度就变成了O(n^2),因为每一层递归都有一个set集合,系统栈空间是n,每一个空间都有set集合。used数组可是全局变量,每层与每层之间公用一个used数组,所以空间复杂度是O(n + n),最终空间复杂度还是O(n)
332.重新安排行程 - Hard (跳过)
题目链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
给你一份航线列表 tickets ,其中 tickets[i] = [fromi, toi] 表示飞机出发和降落的机场地点。请你对该行程进行重新规划排序。
所有这些机票都属于一个从 JFK(肯尼迪国际机场)出发的先生,所以该行程必须从 JFK 开始。如果存在多种有效的行程,请你按字典排序返回最小的行程组合。
例如,行程 ["JFK", "LGA"] 与 ["JFK", "LGB"] 相比就更小,排序更靠前。
假定所有机票至少存在一种合理的行程。且所有的机票 必须都用一次 且 只能用一次。
51. N皇后 - Hard (看Carl视频大致搞懂了)
题目链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
思路:二维数组回溯,时间复杂度: O(n!),空间复杂度: O(n)
class Solution {
private:
vector<vector<string>> result;
// n 为输入的棋盘大小
// row 是当前递归到棋盘的第几行了
void backtracking(int n, int row, vector<string>& chessboard) {
if (row == n) {
result.push_back(chessboard);
return;
}
for (int col = 0; col < n; col++) {
if (isValid(row, col, chessboard, n)) { // 验证合法就可以放
chessboard[row][col] = 'Q'; // 放置皇后
backtracking(n, row + 1, chessboard);
chessboard[row][col] = '.'; // 回溯,撤销皇后
}
}
}
bool isValid(int row, int col, vector<string>& chessboard, int n) {
// 检查列
for (int i = 0; i < row; i++) { // 这是一个剪枝
if (chessboard[i][col] == 'Q') {
return false;
}
}
// 检查 45度角是否有皇后
for (int i = row - 1, j = col - 1; i >=0 && j >= 0; i--, j--) {
if (chessboard[i][j] == 'Q') {
return false;
}
}
// 检查 135度角是否有皇后
for(int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {
if (chessboard[i][j] == 'Q') {
return false;
}
}
return true;
}
public:
vector<vector<string>> solveNQueens(int n) {
result.clear();
std::vector<std::string> chessboard(n, std::string(n, '.'));
backtracking(n, 0, chessboard);
return result;
}
};

37. 解数独 - Hard (跳过)
题目链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
编写一个程序,通过填充空格来解决数独问题。
数独的解法需 遵循如下规则:
数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。(请参考示例图)
数独部分空格内已填入了数字,空白格用 '.' 表示。