👻交换排序
- 🎄1、基本思想及特点
- 🎄2、冒泡排序
- 🎄3、快速排序(挖坑法)
- 🎄4、快速排序优化
- 🎊4.1 三数取中法选key
- 🎊4.2 递归到小的子区间时,可以考虑使用插入排序
- 🎄5、 快速排序非递归
- 🎄6、快速排序总结
🎄1、基本思想及特点
基本思想:所谓交换,就是根据序列中两个记录键值的比较结果来对换这两个记录在序列中的位置。
特点:将键值较大的记录向序列的尾部移动,键值较小的记录向序列的前部移动。
🎄2、冒泡排序
冒泡排序(Bubble Sort)是排序算法里面比较简单的一个排序。它重复地走访要排序的数列,一次比较两个数据元素,如果顺序不对则进行交换,并一直重复这样的走访操作,直到没有要交换的数据元素为止。
如图:
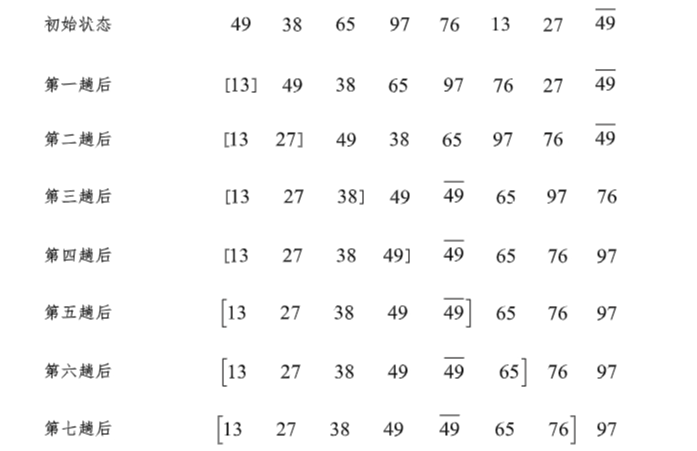
🪄代码示例:
public static void bubbleSort(int[] array) {
//i代表趟数 10 -》 9趟
for (int i = 0; i < array.length-1; i++) {
boolean flg = false;
for(int j = 0;j < array.length-1-i;j++) {
if(array[j] > array[j+1]) {
swap(array,j,j+1);
flg = true;
}
}
//没有交换证明有序了
if(flg == false) {
return;
}
}
}
✌️【冒泡排序的特性总结】
- 冒泡排序是一种非常容易理解的排序
- 时间复杂度:O(N^2)
- 空间复杂度:O(1)
- 稳定性:稳定
🎄3、快速排序(挖坑法)
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法,其基本思想为:任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
🔍快速排序的主要思想可以概括为以下步骤:
1、选择基准元素:从待排序的数组中选择一个元素作为基准元素(通常可以选择数组的第一个元素,但最好的选择是三数取中)。
2、分区:将数组中小于基准元素的元素放在基准元素的左边,大于基准元素的元素放在基准元素的右边,形成两个子数组。
3、递归排序:对基准元素左边的子数组和右边的子数组分别进行递归调用快速排序。
4、合并:将左边子数组、基准元素和右边子数组按顺序合并起来,形成排序后的数组。
如图:
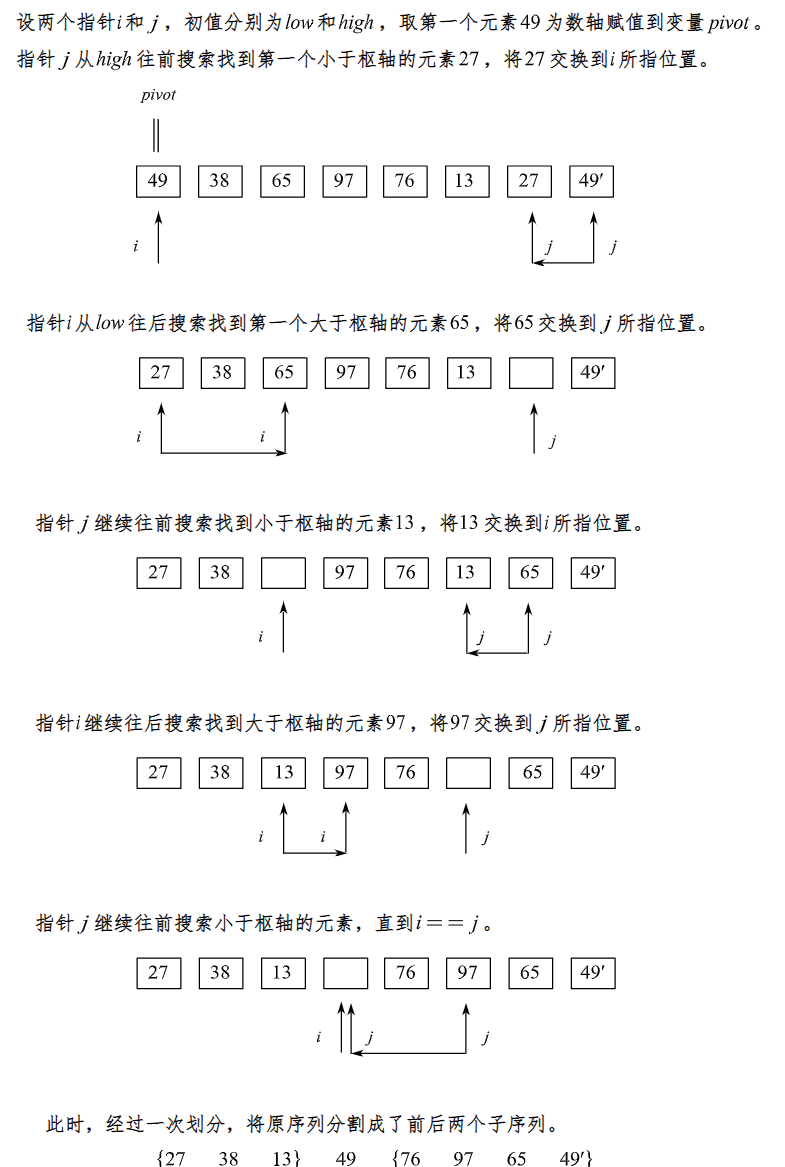

🪄代码示例:
public static void quickSort(int[] array) {
quick(array,0,array.length-1);
}
private static void quick(int[] array,int start,int end) {
if(start >= end) {
return;
}
int pivot = partition(array,start,end);
quick(array,start,pivot-1);
quick(array,pivot+1,end);
}
private static int partition(int[] array, int left, int right) {
int i = left;
int j = right;
int pivot = array[left];
while (i < j) {
while (i < j && array[j] >= pivot) {
j--;
}
array[i] = array[j];
while (i < j && array[i] <= pivot) {
i++;
}
array[j] = array[i];
}
array[i] = pivot;
return i;
}
🎄4、快速排序优化
🎊4.1 三数取中法选key
private static int middleNum(int[] array,int left,int right) {
int mid = left+((right-left) >> 1);
//int mid = (left+right)/2;
if(array[left] < array[right]) {
if(array[mid] < array[left]) {
return left;
}else if(array[mid] > array[right]) {
return right;
}else {
return mid;
}
}else {
if(array[mid] < array[right]) {
return right;
}else if(array[mid] > array[left]) {
return left;
}else {
return mid;
}
}
}
🎊4.2 递归到小的子区间时,可以考虑使用插入排序
public static void insertSort2(int[] array,int start,int end) {
for (int i = start+1; i <= end; i++) {
int tmp = array[i];
int j = i-1;
for (; j >= start ; j--) {
if(array[j] > tmp) {
array[j+1] = array[j];
}else {
break;
}
}
array[j+1] = tmp;
}
}
🪄全部代码示例:
public static void quickSort(int[] array) {
quick(array,0,array.length-1);
}
private static void quick(int[] array,int start,int end) {
if(start >= end) {
return;
}
if(end-start+1 <= 15) {
insertSort2(array, start, end);
return;
}
//1. 三数取中 index是中间大的数字 的 下标
int index = middleNum(array,start,end);
swap(array,index,start);
int pivot = partition(array,start,end);//
quick(array,start,pivot-1);
quick(array,pivot+1,end);
}
private static int partition(int[] array,int left,int right) {
int tmp = array[left];
while (left < right) {
while (left < right && array[right] >= tmp) {
right--;
}
if(left >= right) {
break;
}
array[left] = array[right];
while (left < right && array[left] <= tmp) {
left++;
}
if(left >= right) {
break;
}
array[right] = array[left];
}
array[left] = tmp;
return left;
}
public static void insertSort2(int[] array,int start,int end) {
for (int i = start+1; i <= end; i++) {
int tmp = array[i];
int j = i-1;
for (; j >= start ; j--) {
if(array[j] > tmp) {
array[j+1] = array[j];
}else {
break;
}
}
array[j+1] = tmp;
}
}
private static int middleNum(int[] array,int left,int right) {
int mid = left+((right-left) >> 1);
//int mid = (left+right)/2;
if(array[left] < array[right]) {
if(array[mid] < array[left]) {
return left;
}else if(array[mid] > array[right]) {
return right;
}else {
return mid;
}
}else {
if(array[mid] < array[right]) {
return right;
}else if(array[mid] > array[left]) {
return left;
}else {
return mid;
}
}
}
🎄5、 快速排序非递归
🪄代码示例:
void quickSortNonR(int[] a, int left, int right) {
Stack<Integer> st = new Stack<>();
st.push(left);
st.push(right);
while (!st.empty()) {
right = st.pop();
left = st.pop();
if(right - left <= 1)
continue;
int div = PartSort1(a, left, right);
// 以基准值为分割点,形成左右两部分:[left, div) 和 [div+1, right)
st.push(div+1);
st.push(right);
st.push(left);
st.push(div);
}
}
🎄6、快速排序总结
🔍
- 快速排序整体的综合性能和使用场景都是比较好的,所以才敢叫快速排序
- 时间复杂度:O(N*logN)
- 空间复杂度:O(logN)
- 稳定性:不稳定
🎉OK!今天的分享就到这里了,后面还会分享更多排序算法,敬请关注喔!!!✌️