day16打卡
104. 二叉树的最大深度
- 递归法
- 时间复杂度:O(N),空间复杂度:O(N)
class Solution {
public:
int maxDepth(TreeNode* root) {
if(root == nullptr) return 0;
return 1 + max(maxDepth(root->left), maxDepth(root->right));
}
};
- 迭代法
- 时间复杂度:O(N),空间复杂度:O(N)
class Solution {
public:
int maxDepth(TreeNode* root) {
queue<TreeNode*> q;
if(root != nullptr) q.push(root);
int depth = 0;
while(!q.empty())
{
int size = q.size();
depth++;
for(int i = 0 ; i < size; i++)
{
TreeNode* top = q.front();
q.pop();
if(top->left) q.push(top->left);
if(top->right) q.push(top->right);
}
}
return depth;
}
};
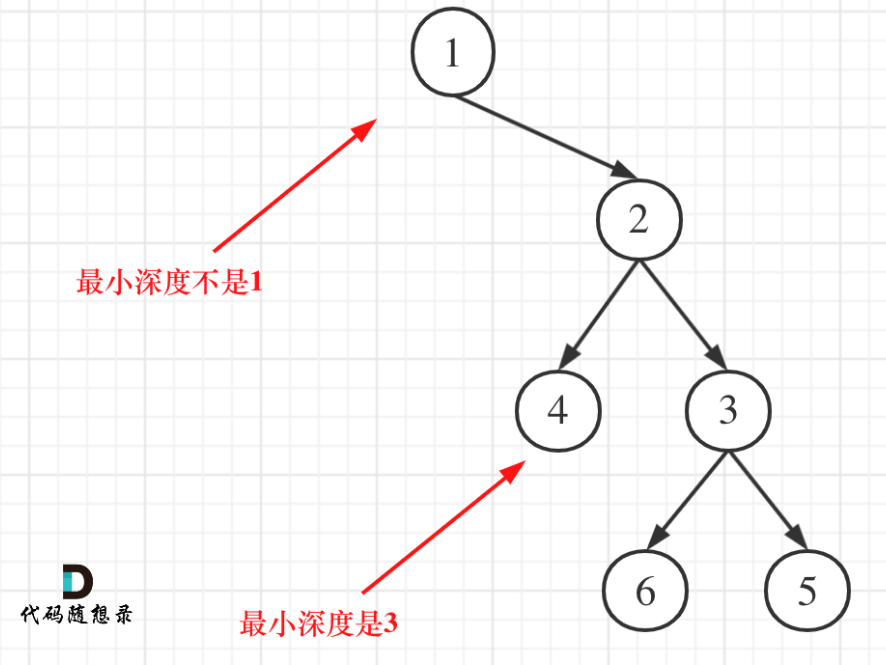
111. 二叉树的最小深度
- 递归法
- 时间复杂度:O(N),空间复杂度:O(N)
注意最小深度即可。
class Solution {
public:
int minDepth(TreeNode* root) {
if(root == nullptr) return 0;
if(root->left == nullptr && root->right != nullptr)
{
return 1 + minDepth(root->right);
}
if(root->left != nullptr && root->right == nullptr)
{
return 1 + minDepth(root->left);
}
return 1 + min(minDepth(root->left), minDepth(root->right));
}
};
- 迭代法
- 时间复杂度:O(N),空间复杂度:O(N)
注意左右节点都为空时就是叶子节点,此时返回depth即可
class Solution {
public:
int minDepth(TreeNode* root) {
queue<TreeNode*> q;
if(root != nullptr) q.push(root);
int depth = 0;
while(!q.empty())
{
int size = q.size();
depth++;
for(int i = 0 ; i < size; i++)
{
TreeNode* top = q.front();
q.pop();
if(top->left) q.push(top->left);
if(top->right) q.push(top->right);
if(top->left == nullptr && top->right == nullptr) return depth;
}
}
return depth;
}
};
222. 完全二叉树的节点个数
-
递归法
-
时间复杂度:O(N),空间复杂度:O(N)
class Solution {
public:
int countNodes(TreeNode* root) {
if(root == nullptr) return 0;
return 1 + countNodes(root->left) + countNodes(root->right);
}
};
- 迭代法
- 时间复杂度:O(N),空间复杂度:O(N)
class Solution {
public:
int countNodes(TreeNode* root) {
queue<TreeNode*> q;
if(root != nullptr) q.push(root);
int count = 0;
while(!q.empty())
{
int size = q.size();
for(int i = 0 ; i < size; i++)
{
TreeNode* top = q.front();
q.pop();
count++;
if(top->left) q.push(top->left);
if(top->right) q.push(top->right);
}
}
return count;
}
};
->left) q.push(top->left);
if(top->right) q.push(top->right);
}
}
return count;
}
};