二叉树，B，B+，B*，R树

二叉树

使用二分结构存储数据，查找数据时，耗时最好可达到O(log2N)。但是二叉树没有平衡的特性，所以在经过一系列的增删后，可能会出现极端的情况，耗时会接近O(N)。

注意，这里的耗时，不仅仅是指查询耗时，还有删除，增加，更新的耗时，因为在确定更新某个节点之前，需要先进行查找

B树

B树在二叉树的基础上增加了平衡的特性，使得树的查询效率维持在O(log2N)，因为他能保持树的基本平衡。

保持树的基本平衡，就意味着同样有N个节点的树，B树比二叉树显得更矮，更胖，磁盘读取次数更少。磁盘读取耗时大概分为几个部分

1. 定位柱面位置时间，大概在0.1s左右
2. 等待时间，即磁头到达指定的柱面后，磁盘还需要旋转到指定的位置，一般磁盘转速在5400rpm，7200rpm左右，也就是一圈大约0.0083s
3. 传输时间，读取到数据后，传输到内存的时间，一般传输一个字节在0.02us左右

可以看到，时间基本耗在了定位柱面的时间上，也就是根据数据指针进行定位的过程，所以我们需要通过合理高效的数据结构，减少第一阶段的次数，而树型结构目前就是效率很高的结构。特别是平衡树。这也就是为什么从磁盘读取的数据所有的存储结构一般用平衡树（一般为多叉，多叉比二叉能更加减少磁盘读写）

特性：

1. 树中每个节点最多含有m个孩子（m>2）
2. 除根节点和叶子节点外，其他每个节点至少有ceil(m/2)个孩子
3. 除叶子节点外，其他节点包含关键字信息，指向关键字数据信息的指针信息以及指向子节点的指针信息
4. 所有叶子节点都出现在同一层

因为根至少有两个孩子，因此第二层起码有两个子节点

假设内含节点最多有m个孩子，则第三层起码有2*ceil(m/2)个子节点

以此类推，第四层起码有2*ceil(m/2)*ceil(m/2)=2*ceil(m/2)^2=2*ceil(m/2)^(4-2)

以此类推，第l层起码有2*ceil(m/2)^(l-2)

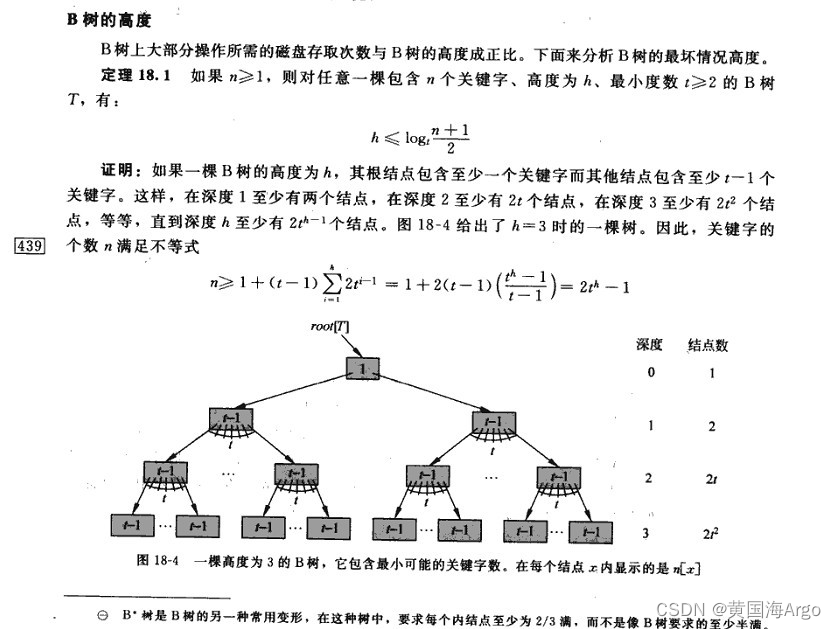
B树的中每个节点存储的内容都是一样的，都包含

1. 存储关键字信息（17表示一个磁盘文件的文件名）
2. 存储关键字指向数据的指针信息（小红方块表示这个17文件内容在硬盘中的存储位置）
3. 存储子节点的指针信息（p1表示指向17左子树的指针）
4. 节点中存储的关键字数可以是几个到几千个，只要不超过磁盘块的大小即可（磁盘块一般为1K~4K左右）

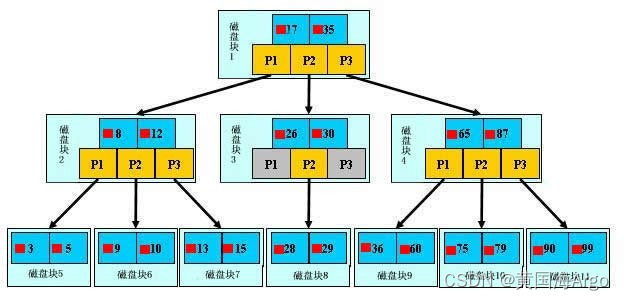
磁盘存储为什么用B树而不用二叉树呢？一个是因为B树是多叉树，而是因为B树是平衡树。两者都是为了节省磁盘IO读写。之后B+树，B*树的优化目的其实也是为了优化磁盘读写来进行设计的，只是优化方式不同。

二叉树到B树

二叉------>多叉

不平衡------->平衡

B+树

B+树是B树的一种变种，所以他们都是平衡多叉树。

B+树通过优化非叶子节点存储的内容来提高单词磁盘IO读取到的关键字信息，从而减少磁盘IO，提高效率。

B+树的存储结构为

非叶子节点：

1. 存储关键字信息（5表示一个磁盘文件的文件名）
2. 存储子节点的指针信息（p1表示指向5左子树的指针）

叶子节点：

1. 存储关键字信息（5表示一个磁盘文件的文件名）
2. 存储关键字指向数据的指针信息
3. 存储指向兄弟节点的指针

可以看到，对于非叶子节点，相对于B树存储三种信息，B+树只需要存储两种信息，单词读取磁盘获取的关键子信息就比B树要多，进而减少磁盘IO

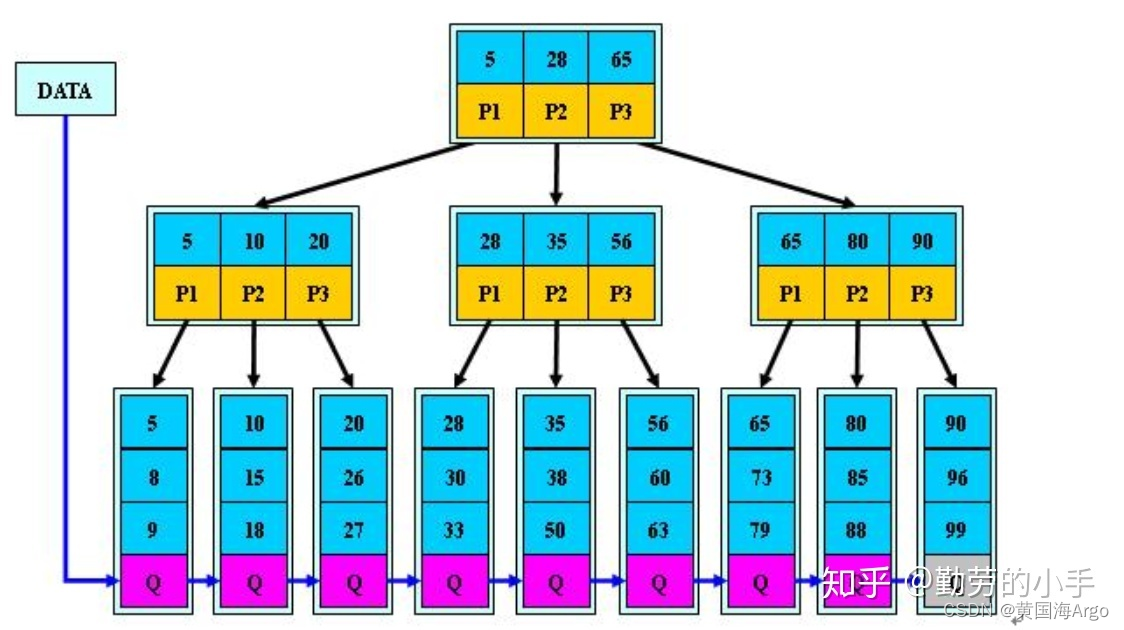
同时B树与B+树的区别还在于，B+树中关键字是会重复的，比如根节点中关键字5，在左节点中也会有5出现，他们是属于一个关键字，并不是两个。而B树中的关键字是不会重复的。

原因：因为B+树的叶子节点要包含所有的关键字信息，才能做到只搜索叶子节点就可以做到全表扫描。

为什么MuSQL的索引存储结构用B+树而不用B树呢？

1. 一个是因为B+树的非叶子节点能存储更多的关键字信息
2. 一个是因为B+树的叶子节点存储指向兄弟节点的指针，使得对于范围查找会更容易
3. 一个是因为叶子节点包含所有的关键字信息，只需要变量叶子节点就可以进行全表扫描。而不用像B树一样需要做中序遍历

知识点

中序遍历：

前序遍历：

后序遍历：

B*树

B*树是B+树的一种变种树。同样他也是平衡多叉树。

对于B+树，他跟B树一样，对子节点的个数有限制，少了需要合并，多了需要分裂

B/B+树特性：

1. 树中每个节点最多含有m个孩子（m>2）
2. 除根节点和叶子节点外，其他每个节点至少有ceil(m/2)个孩子

B*树特性：

1. 树中每个节点最多含有m个孩子（m>2）
2. 除根节点和叶子节点外，其他每个节点至少有ceil(2m/3)个孩子
3. 当新加入节点是，如果兄弟节点未满，则加入到兄弟节点。如果兄弟节点已满，那么自己和兄弟节点各自拆分出1/3部分组成新节点
4. 当删除节点时，如果子节点树少于ceil(2m/3)，那么才会进行组合。

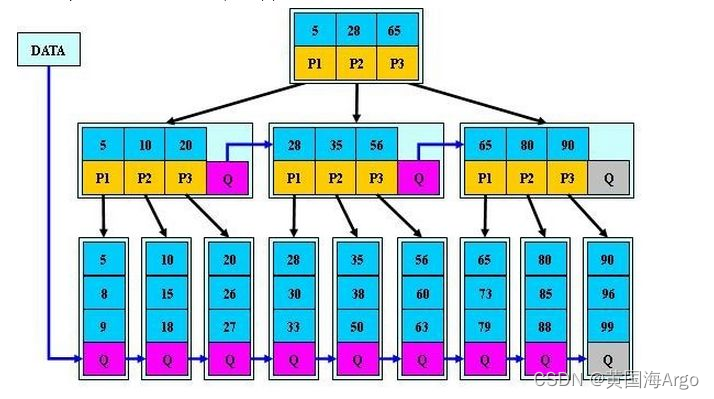
在B*树种，第一个特性不变，对于第二个特性，B*树将其提高到ceil（（2m）/3），减少了分裂的概率，或者叫减少了分裂的频率。同时在分裂时，如果发现兄弟节点未满，那么会将新加入的节点分配到兄弟节点，如果兄弟节点已满，会将自己的1/3和兄弟节点的1/3分割出来，组成一个新节点。前者无疑也减少了节点的拆分，至于子节点树少于一定数量后进行合并过程，其目的也是通过提高合并门槛，降低了合并的概率（频率）。

无论是新增还是删除节点，其目的都是为了提升节点的空间利用率，降低拆分合并概率，也就是降低磁盘IO的次数。

另一方面，B*树的非叶子节点还包含了指向兄弟节点的指针

R树

后补

红黑树

后补