꒰˃͈꒵˂͈꒱ write in front ꒰˃͈꒵˂͈꒱
ʕ̯•͡˔•̯᷅ʔ大家好,我是xiaoxie.希望你看完之后,有不足之处请多多谅解,让我们一起共同进步૮₍❀ᴗ͈ . ᴗ͈ აxiaoxieʕ̯•͡˔•̯᷅ʔ—CSDN博客
本文由xiaoxieʕ̯•͡˔•̯᷅ʔ 原创 CSDN 如需转载还请通知˶⍤⃝˶
个人主页:xiaoxieʕ̯•͡˔•̯᷅ʔ—CSDN博客
系列专栏:xiaoxie的JAVA系列专栏——CSDN博客●'ᴗ'σσணღ*
我的目标:"团团等我💪( ◡̀_◡́ ҂)"( ⸝⸝⸝›ᴥ‹⸝⸝⸝ )欢迎各位→点赞👍 + 收藏⭐️ + 留言📝+关注(互三必回)!
 一.关于二叉树的遍历的总结
一.关于二叉树的遍历的总结
1.使用递归来遍历二叉树
使用递归的方法来遍历二叉树我相信大家应该都没有什么大问题,在这里就不过多的赘述了,直接上代码
1.前序遍历(按照根 -> 左 -> 右)
public void preOrder(TreeNode root) {
if(root == null) {
return;
}
System.out.print(root.val + " ");
preOrder(root.left);
preOrder(root.right);
}2.中序遍历(按照左 -> 根 -> 右)
public void inOrder(TreeNode root) {
if(root == null){
return;
}
inOrder(root.left);
System.out.print(root.val + " ");
inOrder(root.right);
}3.后序遍历(按照左 -> 右 -> 根)
public void postOrder(TreeNode root) {
if(root == null){
return;
}
postOrder(root.left);
postOrder(root.right);
System.out.print(root.val + " ");
}2.迭代解法 (借助栈的思想)
迭代解法本质上是在模拟递归,因为在递归的过程中使用了系统栈,所以在迭代的解法中常用 Stack 来模拟系统栈。
1.前序遍历(按照根 -> 左 -> 右)

首先我们应该创建一个 Stack 用来存放节点,首先我们想要打印根节点的数据,此时 Stack 里面的内容为空,所以我们优先将头结点加入 Stack,然后打印。
之后我们应该先打印左子树,然后右子树。所以先加入 Stack 的就是右子树,然后左子树。
此时你能得到的流程如下:





代码为:
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> list = new ArrayList<>();//打印的容器
if(root == null) return list;
Stack<TreeNode> stack = new Stack<>(); //创建一个栈
TreeNode cur = root;//用cur来遍历二叉树
while (!stack.isEmpty() || cur != null) {
while (cur != null) {
list.add(cur.val);
stack.push(cur);
cur = cur.left;
}
TreeNode top = stack.pop();
cur = top.right;
}
return list;
}
}OJ练习为144. 二叉树的前序遍历 - 力扣(LeetCode)
2.中序遍历 按照(左 ->根 -> 右)
尽可能的将这个节点的左子树压入 Stack,此时栈顶的元素是最左侧的元素,其目的是找到一个最小单位的子树(也就是最左侧的一个节点),并且在寻找的过程中记录了来源,才能返回上层,同时在返回上层的时候已经处理完毕左子树了。当处理完最小单位的子树时,返回到上层处理了中间节点。(如果把整个左中右的遍历都理解成子树的话,就是处理完 左子树->中间(就是一个节点)->右子树)同理创建一个 Stack,然后按 左 中 右的顺序输出节点,只是输出的顺序改变了这里直接上代码
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> list = new ArrayList<>();
TreeNode cur = root;
Stack<TreeNode> stack = new Stack<>();
while(cur != null || !stack.isEmpty()){
while(cur != null) {
stack.push(cur);
cur = cur.left;
}
TreeNode top = stack.pop();
list.add(top.val);
cur = top.right;
}
return list;
}
}OJ练习为94. 二叉树的中序遍历 - 力扣(LeetCode)
3. 中序遍历 按照(左 ->右 -> 根 )
方法1
- 前序遍历的过程 是 根左右。
- 将其转化成 根右左。也就是压栈的过程中优先压入左子树,在压入右子树。
- 然后将这个结果返回来,这里是利用栈的先进后出倒序打印
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
Deque<TreeNode> stack = new LinkedList<>();
LinkedList<Integer> ans = new LinkedList<>();
if (null == root) return ans;
stack.addFirst(root);
while(!stack.isEmpty()) {
TreeNode node = stack.removeFirst();
ans.addFirst(node.val);
if (null != node.left) {
stack.addFirst(node.left);
}
if (null != node.right) {
stack.addFirst(node.right);
}
}
return ans;
}
}方法2.
栈遍历版本: 建议先做中序遍历,后序只是在中序上多了一些操作。
与中序的不同之处在于:
- 中序遍历中,从栈中弹出的节点,其左子树是访问完了,可以直接访问该节点,然后接下来访问右子树。
- 后序遍历中,从栈中弹出的节点,我们只能确定其左子树肯定访问完了,但是无法确定右子树是否访问过。
因此,我们在后序遍历中,引入了一个prev来记录历史访问记录。
- 当访问完一棵子树的时候,我们用prev指向该节点。
- 这样,在回溯到父节点的时候,我们可以依据prev是指向左子节点,还是右子节点,来判断父节点的访问情况。
class Solution{
public List<Integer> method1(TreeNode root) {
List<Integer> ans=new LinkedList<>();
Stack<TreeNode> stack=new Stack<>();
TreeNode prev=null;
//主要思想:
//由于在某颗子树访问完成以后,接着就要回溯到其父节点去
//因此可以用prev来记录访问历史,在回溯到父节点时,可以由此来判断,上一个访问的节点是否为右子树
while(root!=null||!stack.isEmpty()){
while(root!=null){
stack.push(root);
root=root.left;
}
//从栈中弹出的元素,左子树一定是访问完了的
root=stack.pop();
//现在需要确定的是是否有右子树,或者右子树是否访问过
//如果没有右子树,或者右子树访问完了,也就是上一个访问的节点是右子节点时
//说明可以访问当前节点
if(root.right==null||prev==root.right){
ans.add(root.val);
//更新历史访问记录,这样回溯的时候父节点可以由此判断右子树是否访问完成
prev=root;
root=null;
}else{
//如果右子树没有被访问,那么将当前节点压栈,访问右子树
stack.push(root);
root=root.right;
}
}
return ans;
}
}OJ练习为145. 二叉树的后序遍历 - 力扣(LeetCode)
二.关于二叉树子树的问题
1.100. 相同的树 - 力扣(LeetCode)

要想知道两棵树是否相同,首先我们需要比较结构是否相同,然后再比较值是否相同,同样也可以分为递归和迭代两种方法
1.递归方法
class Solution {
public boolean isSameTree(TreeNode p, TreeNode q) {
if(p == null && q == null) return true;
if(p == null && q != null || p != null && q == null) return false;
if(p.val != q.val) return false;
return isSameTree(p.left,q.left) && isSameTree(p.right,q.right);
}2.迭代的方法
class Solution {
public boolean isSameTree(TreeNode p, TreeNode q) {
if(p == null && q == null) return true;
if (p == null || q == null) return false;
Queue<TreeNode> queue = new LinkedList<TreeNode>();
queue.offer(p);
queue.offer(q);
while(!queue.isEmpty()) {
p = queue.poll();
q = queue.poll();
if(p == null && q == null) continue;
if((p == null || q == null) || p.val != q.val)
return false;
queue.offer(p.left);
queue.offer(q.left);
queue.offer(p.right);
queue.offer(q.right);
}
return true;
}
}通过借助队列来判断两棵树的结构和节点的值是否相同,需要注意的是两种方法的时间复杂度都为O(n)。
2.572. 另一棵树的子树 - 力扣(LeetCode)
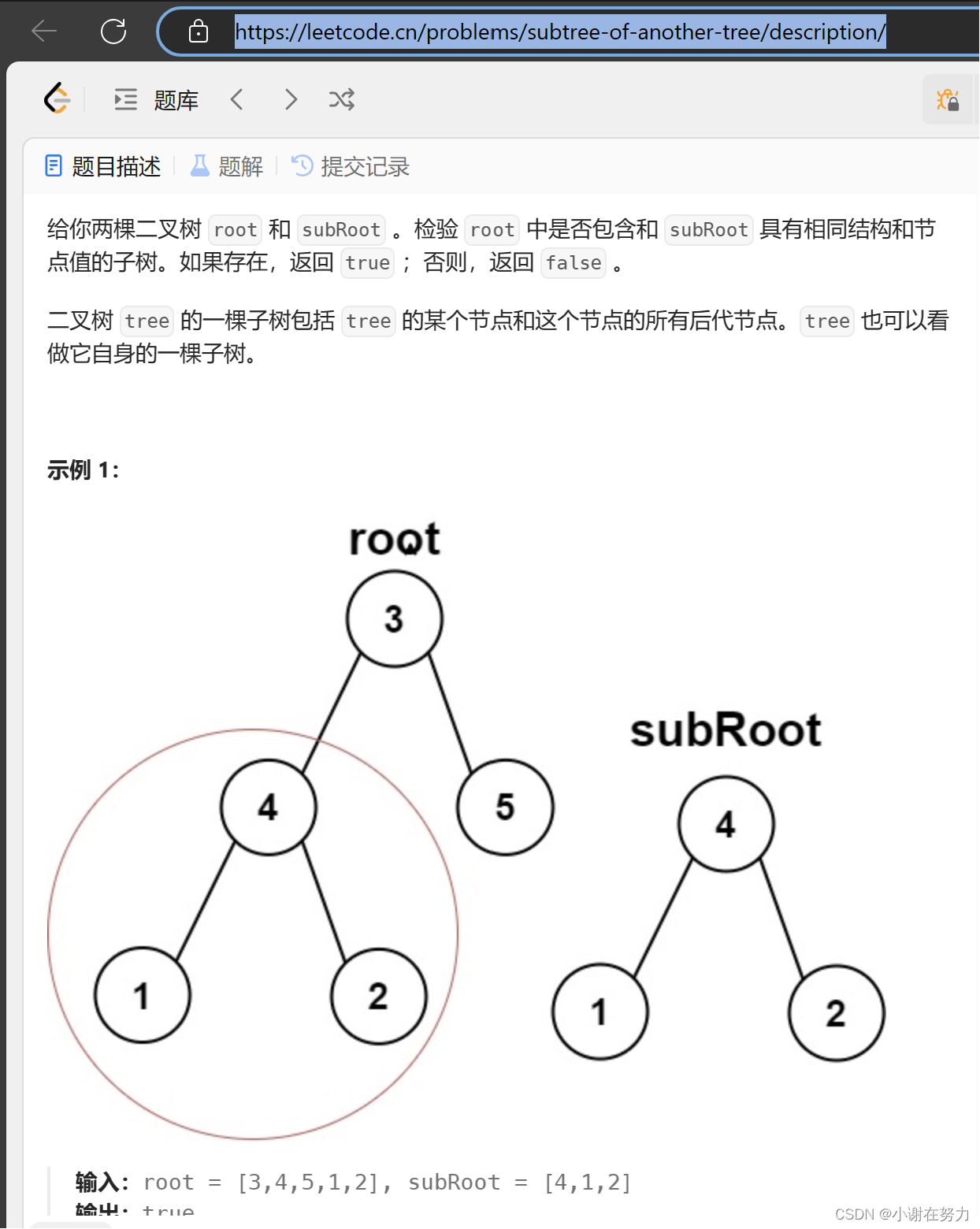 主要思路:将是否为子树的问题转换成是否相等的问题
主要思路:将是否为子树的问题转换成是否相等的问题
class Solution {
public boolean isSubtree(TreeNode root, TreeNode subRoot) {
if(root == null) return false;
if(isSameTree(root,subRoot)) return true;//判断中是否相同
if(isSubtree(root.left,subRoot.left)) return true;//判断左子树是否相同
if(isSubtree(root.right,subRoot.right)) return true;//判断右子树是否相同
return false;
}
private boolean isSameTree(TreeNode root, TreeNode subRoot) {
if(root == null && subRoot == null) return true;
if(root == null && subRoot != null ||root != null && subRoot == null) return false;
if(root.val != subRoot.val) return false;
return isSameTree(root.left,subRoot.left) && isSameTree(root.right,subRoot.right);
}
}其中需要注意的是
判断两个树是否相等的三个条件是与的关系,
即当前两个树的根节点值相等
并且,s的左子树和 r 的左子树相等;
并且,s 的右子树和 r 的右子树相等
判断s 是否为 r的子树的三个条件是或的关系
即当前两棵树相等
或者,s 是 r 的左子树
或者,s 是 r 的右子树
总的来说以上这些方法都是比较简单的暴力或者是递归解法,可能还达不到面试的高度,但学习就是循序渐进的,学会了这些比较基础的解法我相信你在后面学习更优的解法时,肯定更加得心应手
三.二叉树的广度优先搜索的总结(BFS)
1.层序遍历
二叉树的层序遍历问题借助队列可以使用广度优先搜索(BFS)算法来实现这种方法可以保证按层遍历二叉树,先遍历完当前层的节点,再遍历下一层的节点,直到所有节点都被遍历完成
1.基础的二叉树的层序遍历
 题目要求的二叉树的 从上至下 打印(即按层打印),又称为二叉树的 广度优先搜索(BFS)。BFS 通常借助 队列 的先入先出特性来实现。接下来我将一步步的详细讲解
题目要求的二叉树的 从上至下 打印(即按层打印),又称为二叉树的 广度优先搜索(BFS)。BFS 通常借助 队列 的先入先出特性来实现。接下来我将一步步的详细讲解
我们先将根节点放到队列中,然后不断遍历队列。
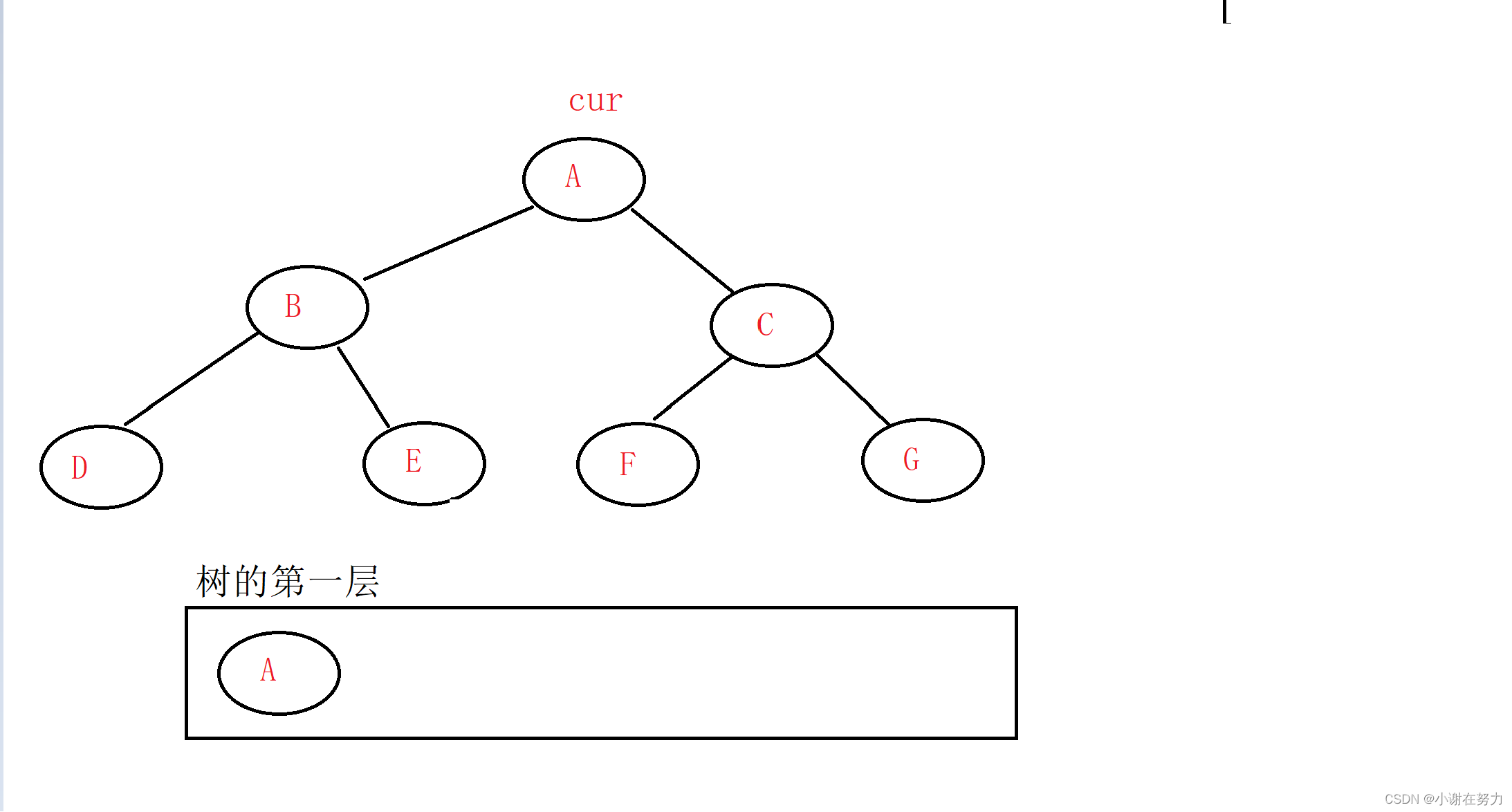
再取出根节点,如果左子树或者右子树不为空,就将他们放入队列中。第一遍处理完后,根节点已经从队列中拿走了,而根节点的两个孩子已放入队列中了,现在队列中就有两个节点即为B和C

同理再取出B和C,如果B的左右孩子不为空,就加入队列,C同理,这样就完成了层层遍历了
 根据上图的解释我们就可以得到如下的代码
根据上图的解释我们就可以得到如下的代码
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> res = new ArrayList<>();
if(root == null) return res;
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);//首先先把根节点加入到队列中去
while(!queue.isEmpty()) {
List<Integer> list = new ArrayList<>();
int size = queue.size();//根据队列的长度来判断是否为同一层的节点
while(size >0) {
TreeNode cur = queue.poll();
list.add(cur.val);
size--;
if(cur.left != null) {//左孩子不为空,就加入到队列中
queue.offer(cur.left);
}
if(cur.right != null) {//右孩子不为空,就加入到队列中
queue.offer(cur.right);
}
}
res.add(list);
}
return res;
}
}
复杂度分析
记树上所有节点的个数为 n。
时间复杂度:每个结点进队出队各一次,故时间复杂度为 O(n)。
空间复杂度:队列中元素的个数不超过 n 个,故空间复杂度为 O(n)。
OJ链接为:102. 二叉树的层序遍历 - 力扣(LeetCode)
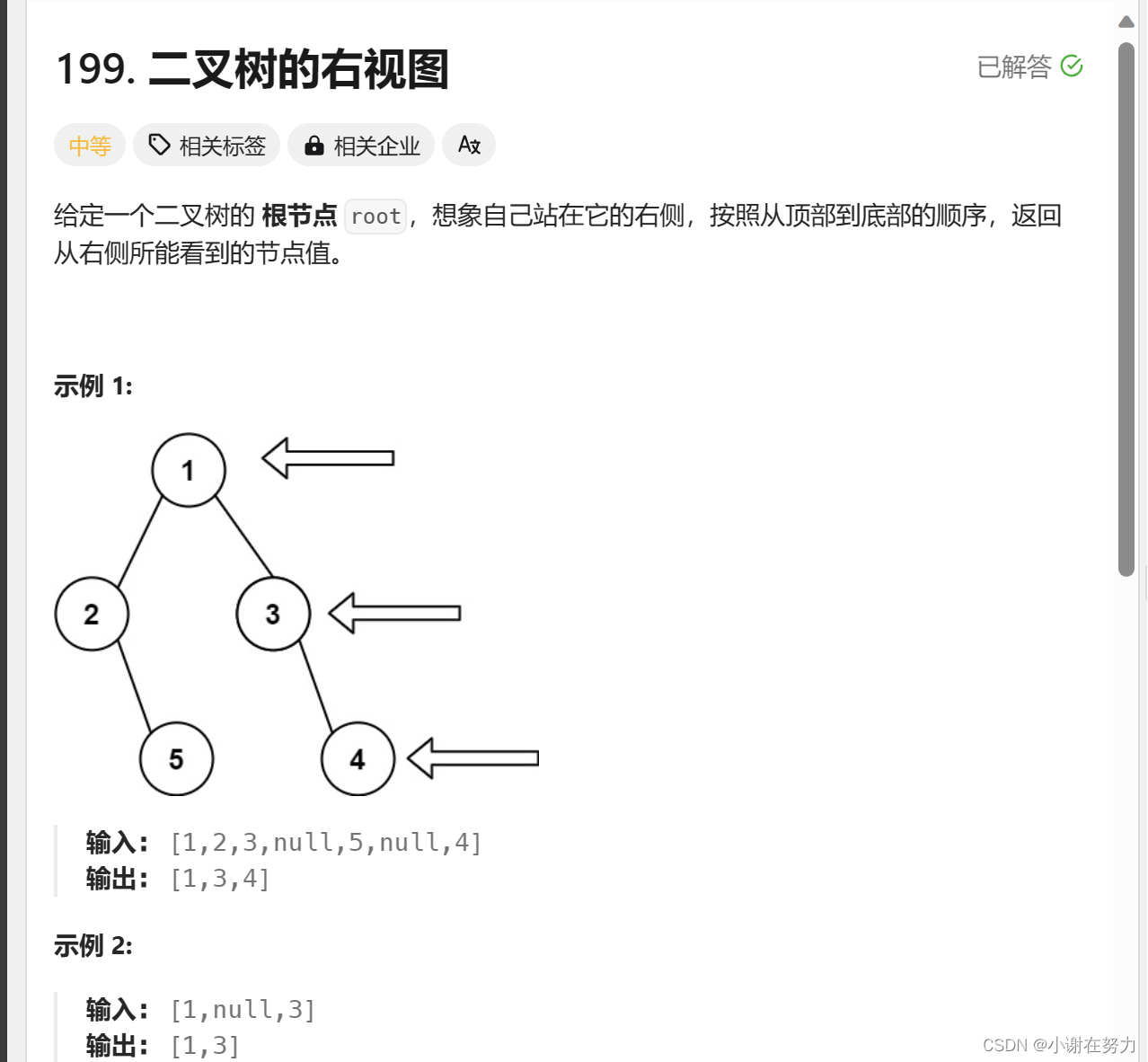
2.层序遍历的应用
这题就看成和上一题一样使用广度优先搜索(BFS),借助队列只不过是这题需要稍微改变一些,输出的是每一层的最后一个。所以可以得到以下的代码
class Solution {
public List<Integer> rightSideView(TreeNode root) {
List<Integer> list = new ArrayList<>();
if(root == null) return list;
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while(!queue.isEmpty()) {
int size = queue.size();//根据队列的长度判断是每一层有多少个节点
while(size > 0) {
TreeNode cur = queue.poll();
if(size == 1) {//如果是每一层的最后一个节点就输出它
list.add(cur.val);
}
size--;
if(cur.left != null) {
queue.offer(cur.left);
}
if(cur.right != null) {
queue.offer(cur.right);
}
}
}
return list;
}
}复杂度分析
时间复杂度 : O(n)。 每个节点最多进队列一次,出队列一次,因此广度优先搜索的复杂度为线性。
空间复杂度 : O(n)。每个节点最多进队列一次,所以队列长度最大不不超过n,所以这里的空间代价为 O(n)。
当然这题也可以用深度优先搜索(DFS),根据题意我们每次都要输出每一层最右边的那一个,然后根据 根 -> 右 -> 左 的顺序这样的话每次第一个搜索的就是最右边的那个节点即每一层的最后一个节点 所以我们可以得到以下代码
class Solution {
List<Integer> list = new ArrayList<>();
public List<Integer> rightSideView(TreeNode root) {
dfs(root,0);
return list;
}
private void dfs(TreeNode root,int depth) {
if(root == null) return;
//先访问 当前节点,再递归地访问 右子树 和 左子树。
if(depth == list.size()) {//如果当前节点所在深度还没有出现在res里,说明在该深度下当前节点是第一个被访问的节点,因此将当前节点加入res中。
list.add(root.val);
}
depth++;
dfs(root.right,depth);
dfs(root.left,depth);
}
}复杂度分析
时间复杂度 : O(n)
空间复杂度 : O(n)
当然这一题无论是DFS 还是 BFS 都可以解这题,时间复杂度和空间复杂度都差不多,只不过DFS更快一点,BFS更容易理解。
OJ链接为:199. 二叉树的右视图 - 力扣(LeetCode) 以上就是博主最近学习二叉树总结的所有内容呢,可能总结的并不是那么全面,不过后续博主学习的更加清楚明白一点,会再将这个总结补全完整,感谢大家的观看。