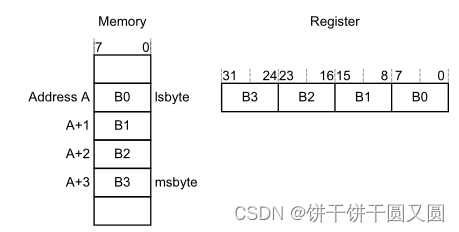
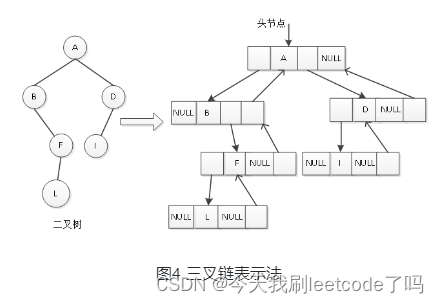
二叉堆树状数组

P3378 【模板】堆

向上调整唯一，向下调整要看孩子

#include<iostream>
#include<iomanip>
#include<vector>
#include<string>
using namespace std;
const int maxn = 1e6 + 3;
int h[maxn], n, op, num, cnt = 0;
void swap(int x, int y) {
    int t = h[x];
    h[x] = h[y];
    h[y] = t;
}
void up(int x) {
    int p = x / 2;
    while (p >= 1&&h[p]>h[x]) {
        swap(x, p);
        x = p;
        p = x / 2;
    }
}
void down(int x) {
    int c = x * 2;
    while (c <= cnt) {
        if (c + 1 <= cnt && h[c + 1] < h[c]) {
            c++;
        }
        if (h[c] < h[x]) {
            swap(c, x);
            x = c;
            c = x * 2;
        }
        else {
            break;
        }
    }
}
void del() {
    h[1] = h[cnt--];
    down(1);
}
int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> op;
        if (op == 1) {
            cin >> num;
            h[++cnt] = num;
            up(cnt);
        }
        else if (op == 2) {
            cout << h[1] << endl;
        }
        else {
            del();
        }
    }
    return 0;
}

P1801 黑匣子

大顶堆小顶堆

大顶堆里的堆顶是最大的元素，小顶堆的是最小的元素，那么i个元素的大顶堆和j个元素的小顶堆拼在一起，堆顶就是指向i+j的数列中第i大的元素

就是说，大顶堆是第i大前面的数，小顶堆是第i大后面的数

插入元素的时候，如果比此时第i大大的话，就直接放入小顶堆中

如果比第i大小，就放入大顶堆，一旦大顶堆的大小超过i,就pop掉大顶堆堆顶的元素，使其进入小顶堆

就是说，小顶堆的堆顶是第i大，但如果是第i大，就说明大顶堆里一定有i-1个元素，即大顶堆里一定只维护着i-1个元素

那就是说，第一次插入的时候，插到小顶堆里，

然后第i次插入的时候，判断插入元素与小顶堆堆顶的大小关系，如果大的话，就不影响第i大，就直接放入小顶堆；否则，插入大顶堆中，并把大顶堆的堆顶插入到小顶堆中并删除，维护大顶堆大小不变，为i-1，这样就能始终保证大顶堆大小为i-1,小顶堆堆顶为第i大的元素

有n次get操作，就说明最后要的是第n大的数，在之前，每次get后都会获得越来越大的第i大的数

每次就往大顶堆里放，一旦大顶堆满了，就溢出进小顶堆里

#include<iostream>
#include<iomanip>
#include<vector>
#include<string>
#include<queue>
using namespace std;
const int maxn = 2e5 + 3;
priority_queue<int>da;
priority_queue<int, vector<int>, greater<int>>xiao;
int m, n, num[maxn], op[maxn], cnt;
int main() {
    cin >> m >> n;
    for (int i = 1; i <= m; i++)cin >> num[i];
    int begin = 1;
    for (int i = 1; i <= n; i++) {//这个就表示此时大顶堆的限度
        cin >> cnt;//表示这个标杆前的数据，都对应的大顶堆大小是i
        for (int j = begin; j <= cnt; j++) {
            da.push(num[j]);
            if(da.size() == i) {//满了i就溢出，就是说最大为i-1
                xiao.push(da.top());
                da.pop();
            }
        }
        cout << xiao.top() << endl;
        begin = cnt + 1;//下一次的起点,
        da.push(xiao.top());//下次要找的就是更大的数据，此时就提前先把大顶堆的容量扩容为i
        xiao.pop();//那么下次检测的时候由于i++,实际上是要i+1才会溢出，就是说这里扩容后
    }//在下次时是不会溢出的，溢出是插入数据后才会溢出，即到达i+1
    return 0;
}

P1090 [NOIP2004 提高组] 合并果子 / [USACO06NOV] Fence Repair G

就是一个哈夫曼树

#include<iostream>
#include<iomanip>
#include<vector>
#include<string>
#include<queue>
using namespace std;
priority_queue<int, vector<int>, greater<int>>q;
int n, ans = 0, temp;
int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> temp;
        q.push(temp);
    }
    while (q.size() != 1) {
        int a = q.top();
        q.pop();
        int b = q.top();
        q.pop();
        q.push(a + b);
        ans += (a + b);
    }
    cout << ans;
    return 0;
}

P2168 [NOI2015] 荷马史诗

类似于哈夫曼树，哈夫曼编码，就是让出现频率最高的字用最短的，出现频率低的用长的

如果是k叉树的话，将k个结点合并为1个，那就是每次减少k-1个结点，一共要将N个结点合并成1个

每次减少k-1个，一共要减少n-1个，所以如果n-1不是k-1的倍数，那么在最后一次的时候就会不够k个，所以就要补充相应数量的空结点来使其达到k-1的倍数

拿普通二叉哈夫曼树举例就是说，一共有n个结点，最后要合并成1个，就是要减少n-1个结点，每次的话，由于是二分，所以每次只会减少1个，所有就要n-1次合并

如果是三分的话，每次会减少两个，那么要减少n-1个结点，就要(n-1)/2次合并

还有就是要注意，是要保证总长度最短，就是说如果权重相同的话，那么优先让高度低的组

而不是让高度高的组，这样的话可以稳住高度差，

因为在哈夫曼树当中，高度就意味着是编码的长度

#include<iostream>
#include<iomanip>
#include<vector>
#include<string>
#include<queue>
using namespace std;
int n, k;
long long temp,ans = 0;
struct node {
    long long w, h;
    node(long long  nw, long long nh) :w(nw), h(nh) {}
};
struct cmp {
    bool operator()(node a, node b) {
        if (a.w != b.w) {
            return a.w > b.w;
        }
        else {
            return a.h > b.h;
        }
    }
};
priority_queue<node, vector<node>, cmp>q;
int main() {
    cin >> n >> k;
    for (int i = 1; i <= n; i++) {
        cin >> temp;
        q.push(node(temp, 1));
    }
    while ((q.size() - 1) % (k - 1)) {
        q.push(node(0, 1));
    }
    while (q.size() != 1) {
        long long maxh = 0, sum = 0;
        for (int i = 1; i <= k; i++) {
            sum += q.top().w;
            maxh = max(maxh, q.top().h);
            q.pop();
        }
        ans += sum;
        q.push(node(sum, maxh + 1));
    }
    cout << ans << endl;
    cout << q.top().h - 1;
    return 0;
}