题目
OJ1229

题目分析
- 题目完全符合栈的特征,后进先出。
- 如果能够熟练使用列表的9种方法那么这道题很容易解出。
题解
a=[]#存衣服
n=int(input())
for i in range(n):
l=list(input().split())#判断每一步的操作
if len(l[0])==2:
a.append(l[1])
else:
while a.pop()!=l[1]:pass
if len(a)==0:print('Empty')
else:print(a[-1])
题目
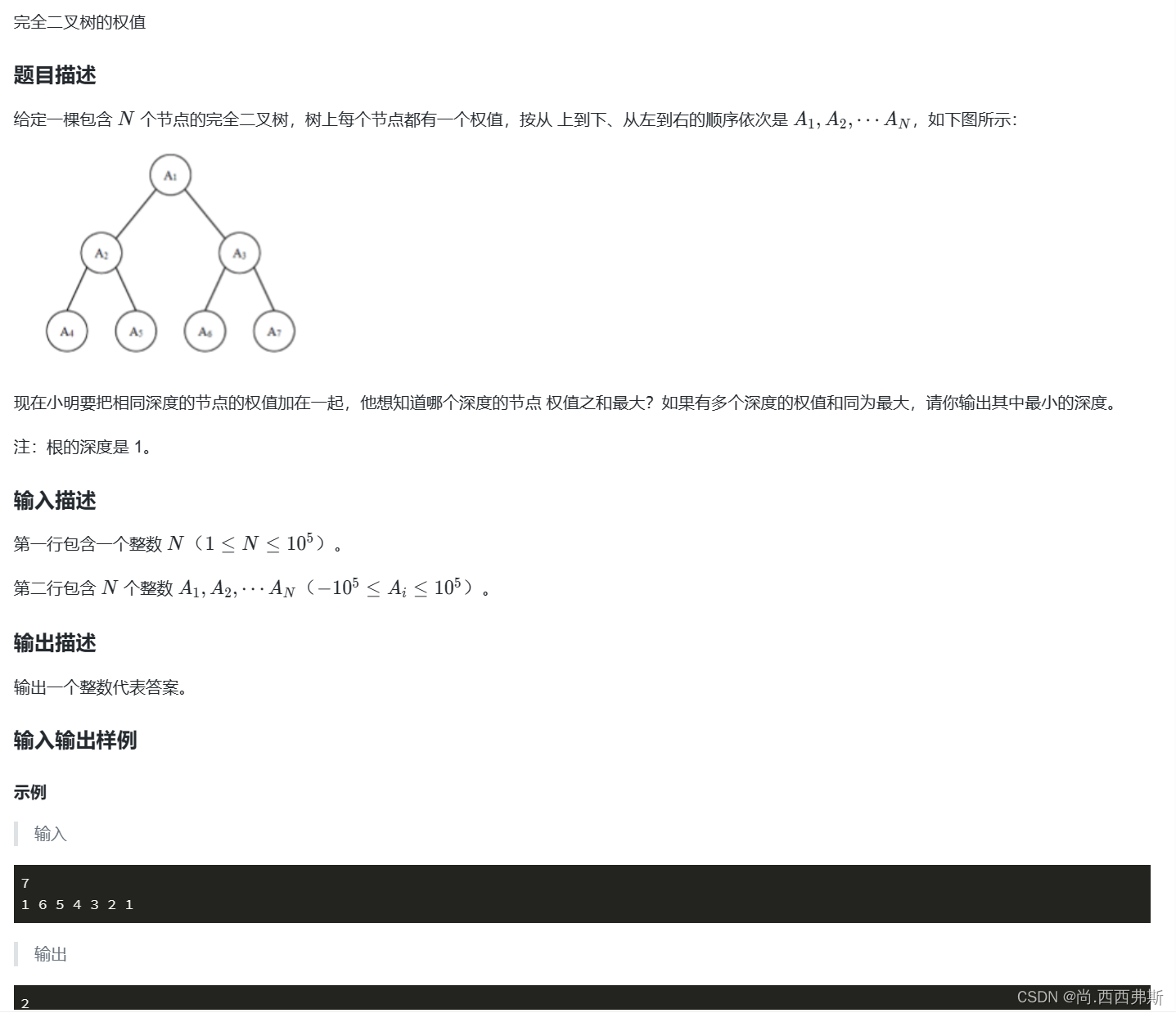
题目分析
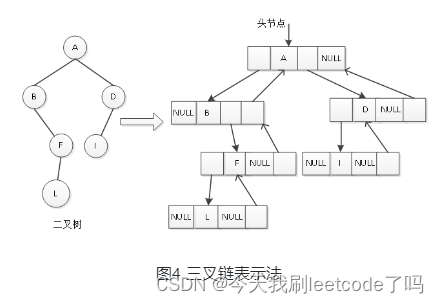
- 输入一层就记录一层的权和,然后输出权和最大的层数,第一步,判断总共有多少层。
以下是 log() 方法的语法:
import math
math.log(x)
math.log(x,base)#以base为底x的对数
参数
x – 数值表达式。
base – 基底
则对此题总共有math.log(n,2)+1层
- 利用列表初始化两个数组,一个用x存储每一个节点的权,s记录每一层的和。
- 利用列表的切片分层求权的和。
- 输出s最大的值的索引。
题解
import math
s=[]
n = int(input())
x= list(map(int, input().split()))
deep=int(math.log(n,2))+1
for i in range(deep):
s.append(sum(x[2**i-1:2**i+2**i-1]))
print(s.index(max(s))+1)