前言
本篇文章介绍了数组的基础定义及使用,并针对数组的基本增删改查做了一些代码示例,下篇文章将讲解基于数组的更高效的方法,比如二分查找、插入排序等。
数组基础
数组定义
int nums[10] = {0};
如上,定义一个int类型的数组,并将每个元素赋初值为0。
实际开发中,我们定义的数组往往是一个我们自己指定的数据类型,如下,定义一个Student结构体,然后定义一个数组。
struct Student {
char *m_name; // 学生名称
int age; // 年龄
int sex; // 性别
};
int main() {
struct Student students[100]; // 定义一个struct Student类型的数组,拥有100个元素
}
数组访问
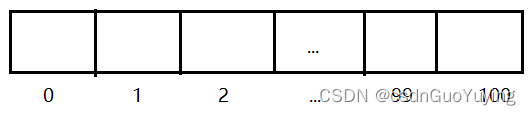
定义一个数组,则产生了上图中结构,数组的每个元素都对应一个下标,我们可以通过下标访问指定的元素。比如
int main() {
int nums[5] = {1, 2, 3, 4, 5};
for (int i = 0; i < 5; ++i) {
printf("%d ", nums[i]);
}
}
这段代码定义了一个有5个元素的int型数组,并将5个元素赋值为1 2 3 4 5;最终通过一个循环打印这个数组。
数组是典型的逻辑上线性,物理上连续的结构。
逻辑上线性——数组中的所有元素都可以通过下标访问,并通过移动下标访问对应的元素。比如nums[2] = 2,nums[2+1] = 3;即可以对下标进行数学运算,从而获取到新下标的元素。与之相反的是后面我们要学习的树、图等无法通过下标访问的数据结构。
物理上连续——即数组在内存中的存储是连续的,并且可以通过对数组某个元素的地址进行运算来访问到其他的元素。与之对应的是链表、树、图等物理上不连续的数据结构。
基本数组算法
数据结构的使用无外乎四个模块:增、删、改、查
增:往数组中添加一个或多个元素
删:往数组中删除一个或多个元素、删除数组中的重复元素等
改:修改数组中某个元素
查:给定一个值,判断该值是否存在于数组中
几乎所有的算法都是围绕这几个基本的算法进行的。算法不同,增删改查的效率就不同。所以说,数据结构 + 算法是程序的核心。
基本算法 —— 查找数组元素
题目描述:给定一个数组,给定一个值,判断该值是否位于数组内
思路:遍历数组,并将每个元素与给定值比较,相等则返回1——表示找到,不等则返回0——表示没找到
/*
* nums: 传入的数组
* size: 数组元素个数
* target: 要比较的目标值
*/
int find_num(int nums[], int size, int target) {
for (int i = 0; i < size; ++i) { // 遍历数组
if (nums[i] == target) {
return 1; // 找到了
}
}
return 0; // 没找到
}
基本算法 —— 获取数组中的最大最小值
题目描述:给定一个数组,找到该数组中的最大最小值并输出
思路:定义变量min、max,分别存储数组中最小与最大值,min初始化为INT_MAX,max初始化为INT_MIN, 遍历数组,如果当前元素 < min,就更新 min = 当前元素;如果当前元素 > max,就更新 max = 当前元素
#define INT_MAX 2147483647
#define INT_MIN -2147483648
void print_max_min(int nums[], int size) {
int max = INT_MIN;
int min = INT_MAX;
for (int i = 0; i < size; ++i) { // 遍历数组
if (nums[i] < min) {
min = nums[i]; // 更新最小值
}
if (nums[i] > max) {
max = nums[i]; // 更新最大值
}
}
printf("max %d min %d\n", max, min);
}