- 332.重新安排行程

class Solution { private LinkedList<String> res; private LinkedList<String> path = new LinkedList<>(); public List<String> findItinerary(List<List<String>> tickets) { Collections.sort(tickets, (a, b) -> a.get(1).compareTo(b.get(1))); path.add("JFK"); boolean[] used = new boolean[tickets.size()]; backTracking((ArrayList) tickets, used); return res; } public boolean backTracking(ArrayList<List<String>> tickets, boolean[] used) { if (path.size() == tickets.size() + 1) { res = new LinkedList(path); return true; } for (int i = 0; i < tickets.size(); i++) { if (!used[i] && tickets.get(i).get(0).equals(path.getLast())) { path.add(tickets.get(i).get(1)); used[i] = true; if (backTracking(tickets, used)) { return true; } used[i] = false; path.removeLast(); } } return false; } } - 51. N皇后

class Solution { List<List<String>> res = new ArrayList<>(); public List<List<String>> solveNQueens(int n) { char[][] chessboard = new char[n][n]; for (char[] c : chessboard) { Arrays.fill(c, '.'); } backTrack(n, 0, chessboard); return res; } public void backTrack(int n, int row, char[][] chessboard) { if (row == n) { res.add(Array2List(chessboard)); return; } for (int col = 0;col < n; ++col) { if (isValid (row, col, n, chessboard)) { chessboard[row][col] = 'Q'; backTrack(n, row+1, chessboard); chessboard[row][col] = '.'; } } } public List Array2List(char[][] chessboard) { List<String> list = new ArrayList<>(); for (char[] c : chessboard) { list.add(String.copyValueOf(c)); } return list; } public boolean isValid(int row, int col, int n, char[][] chessboard) { // 检查列 for (int i=0; i<row; ++i) { // 相当于剪枝 if (chessboard[i][col] == 'Q') { return false; } } // 检查45度对角线 for (int i=row-1, j=col-1; i>=0 && j>=0; i--, j--) { if (chessboard[i][j] == 'Q') { return false; } } // 检查135度对角线 for (int i=row-1, j=col+1; i>=0 && j<=n-1; i--, j++) { if (chessboard[i][j] == 'Q') { return false; } } return true; } } - 37. 解数独

class Solution { public void solveSudoku(char[][] board) { solveSudokuHelper(board); } private boolean solveSudokuHelper(char[][] board){ //「一个for循环遍历棋盘的行,一个for循环遍历棋盘的列, // 一行一列确定下来之后,递归遍历这个位置放9个数字的可能性!」 for (int i = 0; i < 9; i++){ // 遍历行 for (int j = 0; j < 9; j++){ // 遍历列 if (board[i][j] != '.'){ // 跳过原始数字 continue; } for (char k = '1'; k <= '9'; k++){ // (i, j) 这个位置放k是否合适 if (isValidSudoku(i, j, k, board)){ board[i][j] = k; if (solveSudokuHelper(board)){ // 如果找到合适一组立刻返回 return true; } board[i][j] = '.'; } } // 9个数都试完了,都不行,那么就返回false return false; // 因为如果一行一列确定下来了,这里尝试了9个数都不行,说明这个棋盘找不到解决数独问题的解! // 那么会直接返回, 「这也就是为什么没有终止条件也不会永远填不满棋盘而无限递归下去!」 } } // 遍历完没有返回false,说明找到了合适棋盘位置了 return true; } /** * 判断棋盘是否合法有如下三个维度: * 同行是否重复 * 同列是否重复 * 9宫格里是否重复 */ private boolean isValidSudoku(int row, int col, char val, char[][] board){ // 同行是否重复 for (int i = 0; i < 9; i++){ if (board[row][i] == val){ return false; } } // 同列是否重复 for (int j = 0; j < 9; j++){ if (board[j][col] == val){ return false; } } // 9宫格里是否重复 int startRow = (row / 3) * 3; int startCol = (col / 3) * 3; for (int i = startRow; i < startRow + 3; i++){ for (int j = startCol; j < startCol + 3; j++){ if (board[i][j] == val){ return false; } } } return true; } }
代码随想录算法训练营29期|day30 任务以及具体安排
news2026/2/12 11:04:37
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/1409569.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
Spring基于dynamic-datasource实现MySQL多数据源
目录
多数据源实现
引入依赖
yml配置文件
业务代码
案例演示 多数据源实现
引入依赖
<dependency><groupId>com.baomidou</groupId><artifactId>dynamicdatasourcespringbootstarter</artifactId><version>3.5.0</version>
&…
Java玩转《啊哈算法》排序之桶排序
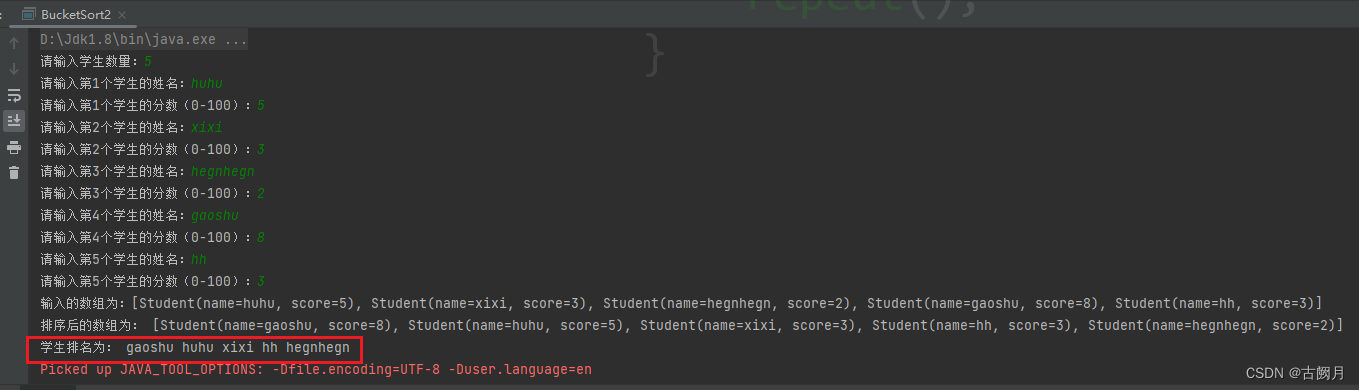
过去心不可得,现在心不可得,未来心不可得 目录在这里 楔子代码地址桶排序代码核心部分优缺点 完整代码演示 升级版核心代码完整代码演示 楔子
大家好!本人最近看了下《啊哈算法》,写的确实不错,生动形象又有趣&#x…
【开源】基于JAVA语言的假日旅社管理系统
目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 系统介绍2.2 QA 问答 三、系统展示四、核心代码4.1 查询民宿4.2 新增民宿评论4.3 查询民宿新闻4.4 新建民宿预订单4.5 查询我的民宿预订单 五、免责说明 一、摘要
1.1 项目介绍
基于JAVAVueSpringBootMySQL的假日旅社…
Java-HashMap如何找落点
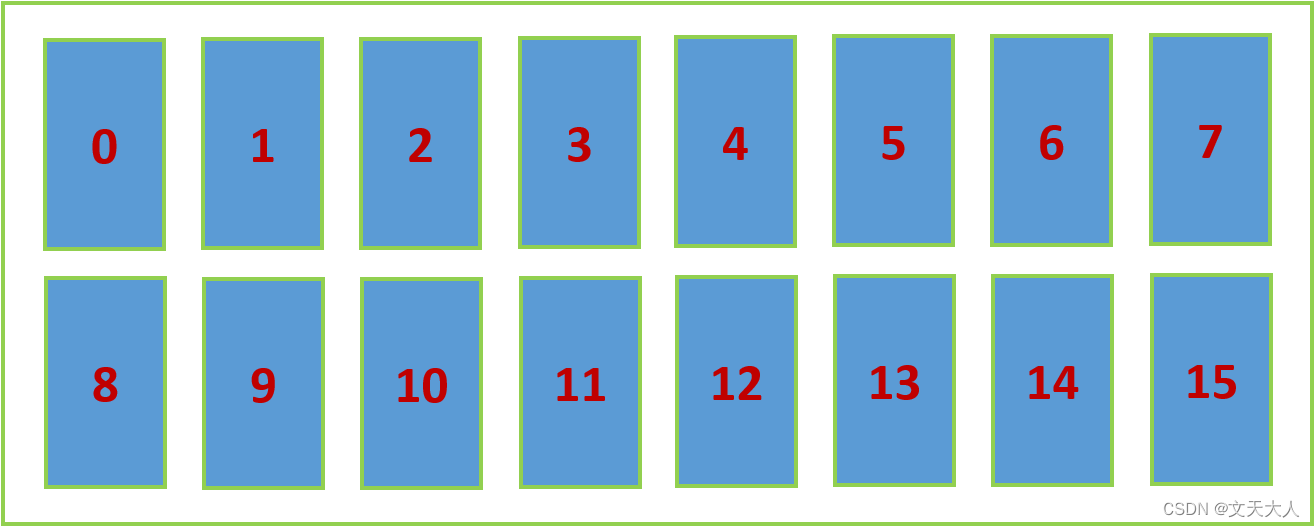
顾名思义,HashMap采用的是哈希方式来找落点,通过数据的某些特征,计算出一个哈希值,然后用哈希值与节点建立映射关系,从而确定这个数据应该在哪个节点上,下图是一个具有16个节点的分布式集群,本文…
JVM篇--垃圾回收器高频面试题
1 你知道哪几种垃圾收集器,各自的优缺点是啥,重点讲下cms和G1,包括原理,流程,优缺点?
1)首先简单介绍下 有以下这些垃圾回收器 Serial收集器: 单线程的收集器,收集垃圾时…
【K8S 云原生】K8S的图形化工具——Rancher
目录 一、rancher概述
1、rancher概念
2、rancher和K8S的区别:
二、实验
1、安装部署
2、给集群添加监控:
3、创建命名空间:
4、创建deployment:
5、创建service:
6、创建ingress:
7、创建hpa
8…
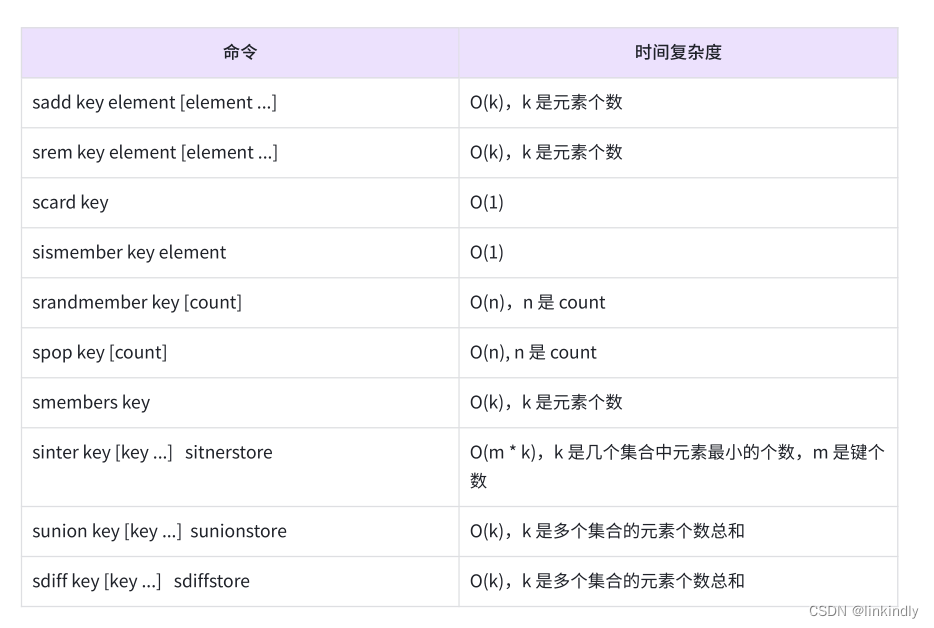
redis—Set集合
目录
前言
1.常见命令
2.使用场景 前言
集合类型也是保存多个字符串类型的元素的,但和列表类型不同的是,集合中1)元素之间是无序的2)元素不允许重复,如图2-24所示。一个集合中最多可以存储22 - 1个元素。Redis 除了支持集合内的增删查改操…
Android SeekBar 进度条圆角
先看下效果图:
之前:
优化后: 之前的不是圆角是clip切割导致的
全代码:
<SeekBarandroid:layout_width"188dp"android:layout_height"wrap_content"android:background"null"android:focusa…
微认证 openEuler社区开源贡献实践
文章目录 1. 开源与开源社区2. openEuler 社区概述3.参与openEuler社区贡献4.openEuler软件包开发Linux软件管理——源码编译 1. 开源与开源社区
Richard Matthew Stallman,1983年9月推出GNU项目,并发起自由软件运动(free software movement或free/open…
【并发】什么是 Future?
🍎个人博客:个人主页
🏆个人专栏:JAVA
⛳️ 功不唐捐,玉汝于成 目录
前言
正文
关键特性和操作包括:
提交任务:
查询完成状态:
等待结果:
取消任务:…
Vue实现图片预览,侧边栏懒加载,不用任何插件,简单好用
实现样式 需求
实现PDF上传预览,并且不能下载 第一次实现:用vue-pdf,将上传的文件用base64传给前端展示 问题: 水印第一次加载有后面又没有了。当上传大的pdf文件后,前端获取和渲染又长又慢,甚至不能用 修…
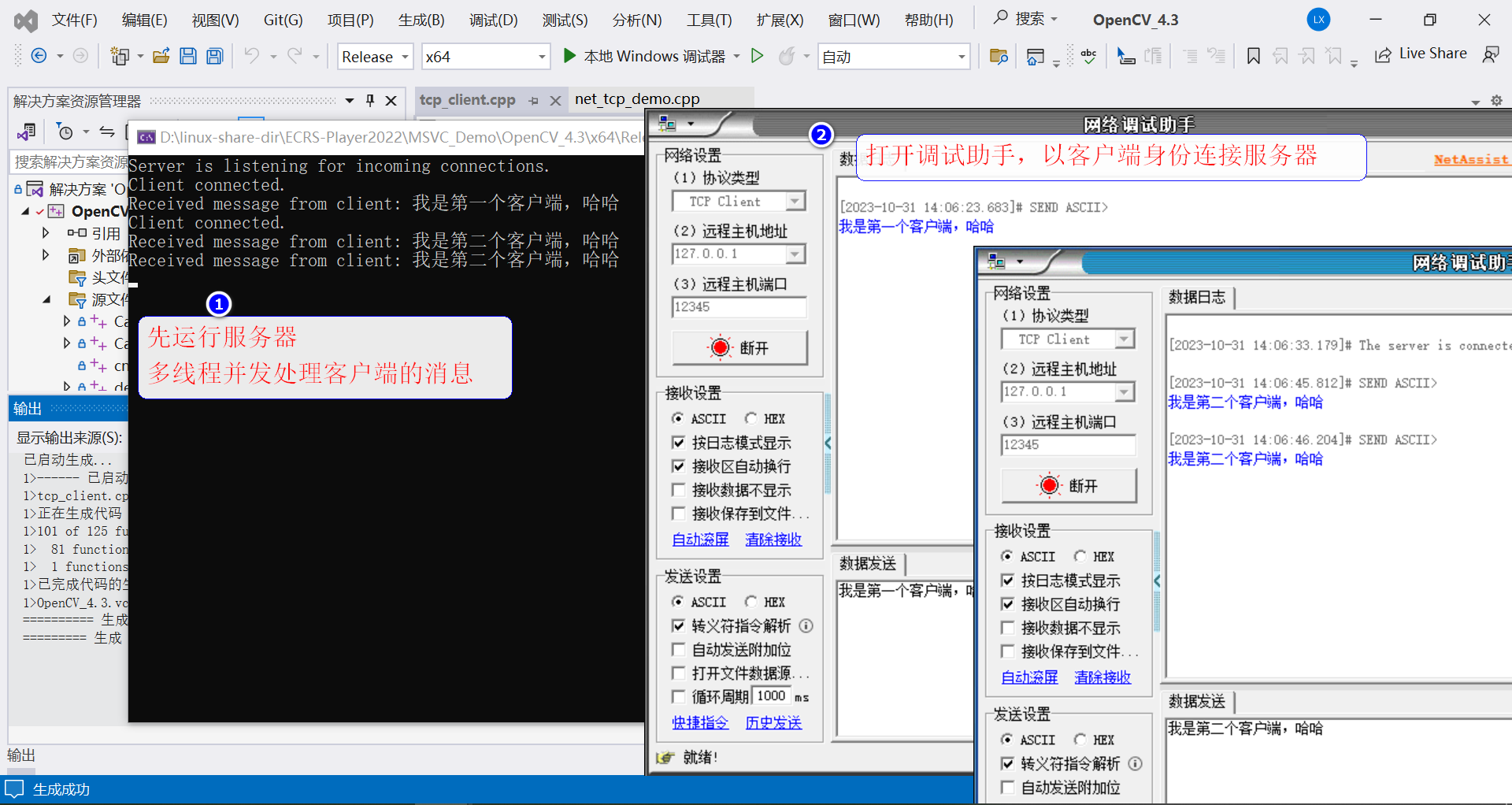
Windows下网络编程(win32API+VS2022)
一、开发环境
我这里介绍下我用的环境安装过程。 所有版本的VS都可以的。
我当前环境是在Windows下,IDE用的是地表最强IDE VS2022。
下载地址:https://visualstudio.microsoft.com/zh-hans/downloads/ 因为我这里只需要用到C和C语言编程,那…
SRC实战 | 小白SRC找到的第一个SQL注入
本文由掌控安全学院 - zbs投稿
一、漏洞说明
xxxxx公司后台存在SQL注入,后端数据库为Mysql 【显错位2,4,6】
漏洞已提交平台,后台的开发商提供给了很多公司,搜一下资产就有很多公司都没有修复该漏洞。
二、漏洞挖掘…
Java Web(四)--JavaScript
介绍
JavaScript 教程 JavaScript 能改变 HTML 内容,能改变 HTML 属性,能改变 HTML 样式 (CSS),能完成页面的数据验证; JS 需要运行浏览器来解析执行JavaScript 代码; JS 是 Netscape 网景公司的产品…
SSL证书 DV、OV、EV等级的证书适用群体
DV(Domain Validation,域名验证)证书
特点:DV证书是最基础的SSL/TLS证书类型,仅验证申请证书的实体是否对该域名有控制权。验证过程相对简单快速,通常只需要验证域名的所有权即可。
适用人群:…
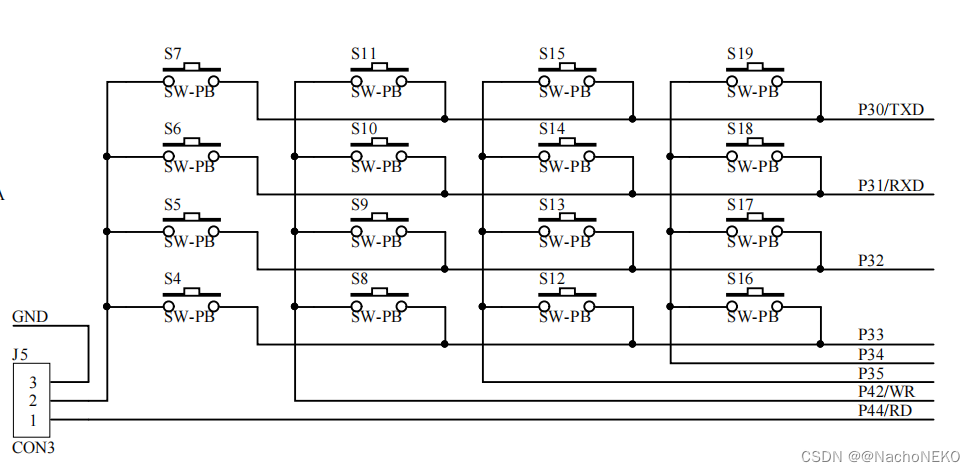
蓝桥杯备战——2.矩阵键盘
1.分析原理图 由上图可以看到若J5跳线帽接地,就S4~S7就可以当做四路独立按键,若接到P44,则就是4*4的矩阵键盘。
2.独立按键处理
相对传统的按键延时消抖方案,这里我采用更高效,更经典,更偏向产品级应用的…
2016年认证杯SPSSPRO杯数学建模B题(第一阶段)低分辨率下看世界全过程文档及程序
2016年认证杯SPSSPRO杯数学建模
B题 低分辨率下看世界
原题再现: 数码摄像技术被广泛使用于多种场合中。有时由于客观条件的限制,拍摄设备只能在较低的分辨率下成像。为简单起见,我们只考虑单色成像。假设成像的分辨率为 32 64,…
一文读懂mysql的锁
提起mysql的锁,你是否会似懂非懂,最常听人提起的就是乐观锁,悲观锁、排他锁、共享锁 悲观锁是用
select c form T for update然后等待提交实现的,但是你知道吗,其实排他锁和悲观锁其实是一回事!࿰…