顾名思义，HashMap采用的是哈希方式来找落点，通过数据的某些特征，计算出一个哈希值，然后用哈希值与节点建立映射关系，从而确定这个数据应该在哪个节点上，下图是一个具有16个节点的分布式集群，本文后续所有示例均以下图为前提

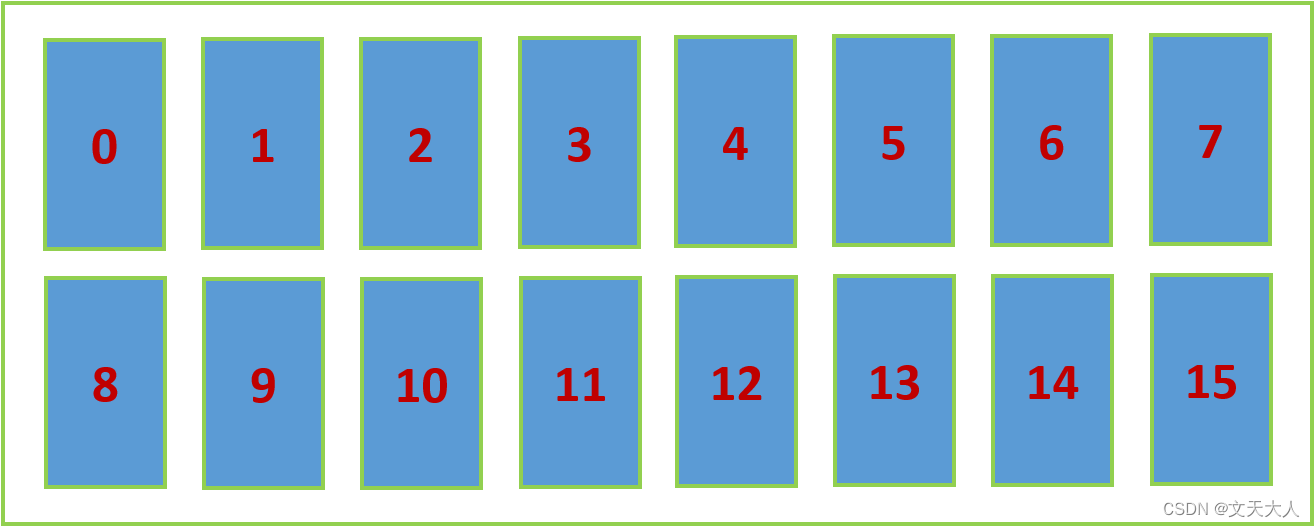
假设有一个对象A，它的哈希值是312，那么对象A应该落到8那个节点上，因为312%16=8，同理：
如果对象A的哈希值=15，那么A在15节点上，因为15 % 16=15
如果对象A的哈希值=16，那么A在0节点上，因为16 % 16=0
如果对象A的哈希值=19960312，那么A应该在8那个节点上，因为19960312 % 16=8

通过上述除法的方式，给定一个任意值，用该值除以16，求余数，这个余数必定小于16，从而对任意值进行落点（落到指定的节点）

那么是不是可以有这样一种设想：“假设我有一个算法，给定任意一个数字，代入该算法，如果结果必定小于16”，那么我就可以说该算法可以用来求数据落点？ 没错，这种设想是一个真命题，是正确的，在Java中，Joshua Bloch使用了下面的方式实现了该算法，该算法共分下面几个步骤：

步骤1).假设对象A的哈希值=312（一定要记住这个数字，因为是我们HR的生日，植树节那天）

步骤2).用312 & 15 = 8
|----为什么要与15，与16不行吗？不行，因为节点最多16个，15的2进制是1111，能确保任何数&15之后结果必定0到15，与16结果有可能得出16
|----为什么要与操作，或操作不行吗？不太行，这个算法中的与操作就是为了分割位数，保留后多少位，或的话根本不沾边，根本不能保证结果<=15
|----既然得出了8，那把A放到8号节点了是不是就可以了？不行，算法截至到目前，还不完善，因为&15，就意味着任何哈希值，都截取最低4位再与15，假设2个hash值的低四位相同，那么必定hash冲突，最终落到同一个点，例如504和312，二进制分别如下：

hash值	二进制
504	1 1111 1000
312	1 0011 1000

他俩低4位都是1000，与15之后，将产生相同的结果，因为高4位没参与计算，导致落点位置相同，冲突的概率很大

步骤3).如何才能使高位也参与计算呢？方法万千，只要让高4位参与计算就可以了，至于什么计算无所谓（与或非啥的都行），下面我们使用了右移4位的方式让高位参与计算
504：
原值为：1 1111 1000
右移四：0 0001 1111
这俩值再 & 一下结果为：0 0001 1000
该结果低四位再 & 15=1000&1111=十进制8（落到8号点）
312：
原值为：1 0011 1000
右移四：0 0001 0011
这俩值再 & 一下结果为：0 0001 0000
该结果低四位再 & 15=0000&1111=十进制0（落到0号点）

这个时候我们发现通过右移4为之后再&自身，最终低4位的结果就不一样了，这样，低4位再&步骤3的15，就减少了hash冲突

总结：
1. 在Java的HashMap源码中，步骤3对应的就是static final int hash方法，不过该方法右移16位，本示例右移4位
2. 求落点的方式，传统上用求余的方式，而在Java的HashMap中，使用的是&[数组长度-1]的方式，也就是本文的步骤2，对应HashMap源码是getNode方法中的tab[(n - 1) & hash])这段代码
3. 右移N位与本算法的关系：假设有2个hash值，它们都小于2的N次方，那么本算法不能解决hash冲突，在本文的步骤3中，N=4，那么2的4次方=16，如果两个hash值都小于16，那么通过右移再与自身，然后&15，得到的落点是一样的，例如14和13
14=(14 & (14>>>4))& 15=落点为0
13=(13 & (13>>>4))& 15=落点为0
但是如果大于16，则大概率落点不一样，例如17和18
17=(14 & (14>>>4))& 15=落点为1
18=(13 & (13>>>4))& 15=落点为0
4. HashMap中为什么没有采用传统的求余找落点的方式，而是采用这种方式？在注释中它也提及了，是为了提高效率（xor指令使用方式），所以在解决hash冲突的质量上进行了一定的降低，言外之意就是这种方式没有求余的方式落点质量高，这点从总结3中就能看得出来，需要hash值的范围做配合