​

参考资料

GeoGebra系列教程3——GGB与正态分布密度曲线_哔哩哔哩_bilibili

我要开始学习啦，吼吼~~~

---

准备工作

https://www.geogebra.org/download

选择GeoGebra 经典 6

---

详细步骤

设计思路	具体操作
设计积分区间【a,b】	创建滑动条a∈[-5,5]，增量是0.01 创建滑动条b∈[-5,5]，增量是0.01
设计期望与方差	创建滑动条μ∈[-5,5]，增量是0.01 创建滑动条$\sigma$∈[-5,5]，增量是0.01
绘制正态分布曲线	输入公式$\frac{1}{\sqrt{2\pi }}{e}^{\frac{(x-\mu {)}^2}{2{\sigma }^2}}$
积分函数（不是累计分布函数）
描点	(μ + σ, f(μ + σ)) (μ + 2σ, f(μ + 2σ)) (μ + 3σ, f(μ + 3σ)) (μ - σ, f(μ - σ)) (μ - 2σ, f(μ - 2σ)) (μ - 3σ, f(μ - 3σ)) (μ - σ, 0) (μ - 2σ, 0) (μ - 3σ, 0) (μ + σ,0) (μ + 2σ, 0) (μ + 3σ, 0)
连线	将上述的点连成线段
复选框	显示或者隐藏线段

---

步骤对应的操作

一些输入方法

输入变量	输入方法
π	Pi
$\sigma$、μ	Geogebra的键盘输入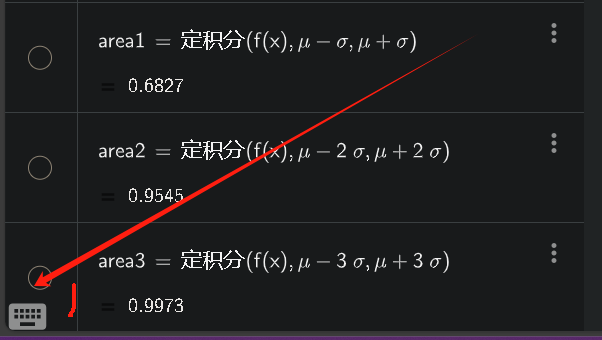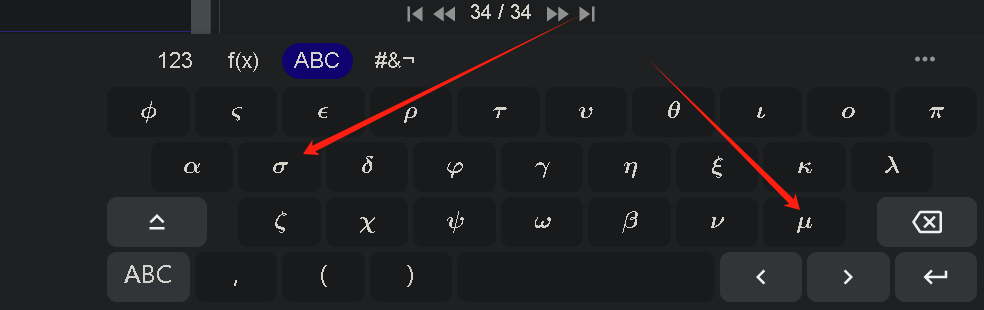
自定义变量area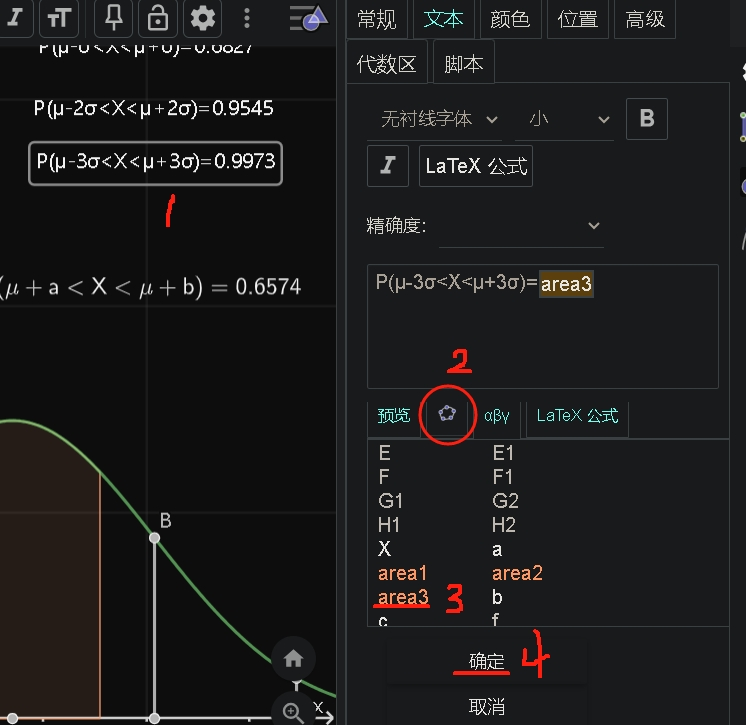
积分	area2=定积分(f(x),μ-2 σ,μ+2 σ)
函数上取一点	H1=(μ-3 σ,f(μ-3 σ))

线段的用法

为什么会需要使用线段呢？
因为例如我们想求$P(\mu -\sigma <X<\mu +\sigma )$的数值
那么就需要把概率密度函数$(\mu -\sigma <X<\mu +\sigma$用两条线段给围起来。
这个时候可以使用

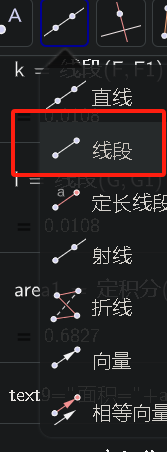
效果如下：

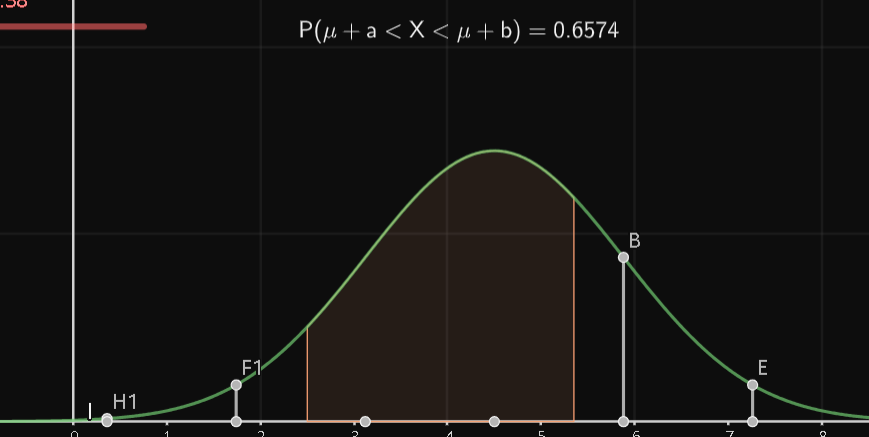
复选框的用法

为什么要使用复选框呢？例如：
我们相求：
我们想求①$P(\mu -\sigma <X<\mu +\sigma )$的数值
我们想求②$P(\mu -2\sigma <X<\mu +2\sigma )$的数值
我们想求③$P(\mu -3\sigma <X<\mu +3\sigma )$的数值
那怎么在图上表示的，如果都要表示，那就是6个线段，那就太乱了对不对。
所以我们
想求①②③的任何一个的时候，就让他显示，
不需要求的时候就让他不显示。

那么怎么实现上述逻辑呢？
一、积分表达式
二、复选框
三、积分表达式的显示条件设定为复选框名称。
如果复选框为true，即表示满足显示条件。
如果复选框为False，即表示不满足显示条件。
具体步骤如下：
①新建一个复选框

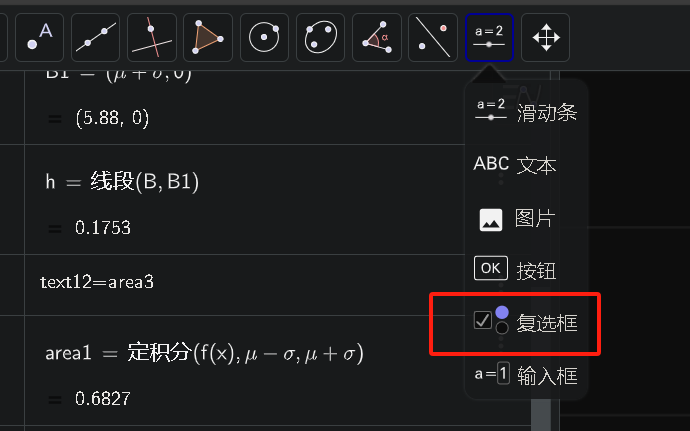
②在坐标图中选择一个位置左键单击
出来一个对话框，然后选择
area1=定积分(f(x),μ-σ,μ+σ)
如下：

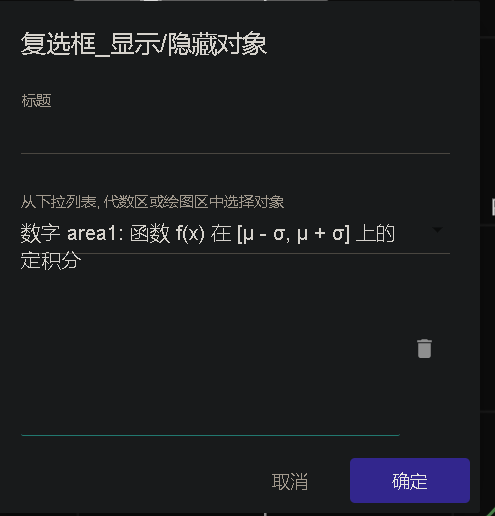
然后我们会看到

说明这个复选框的变量为d
③我们找到这个公式，左键点击三点，选择“设置”

④我们把显示条件设置为d

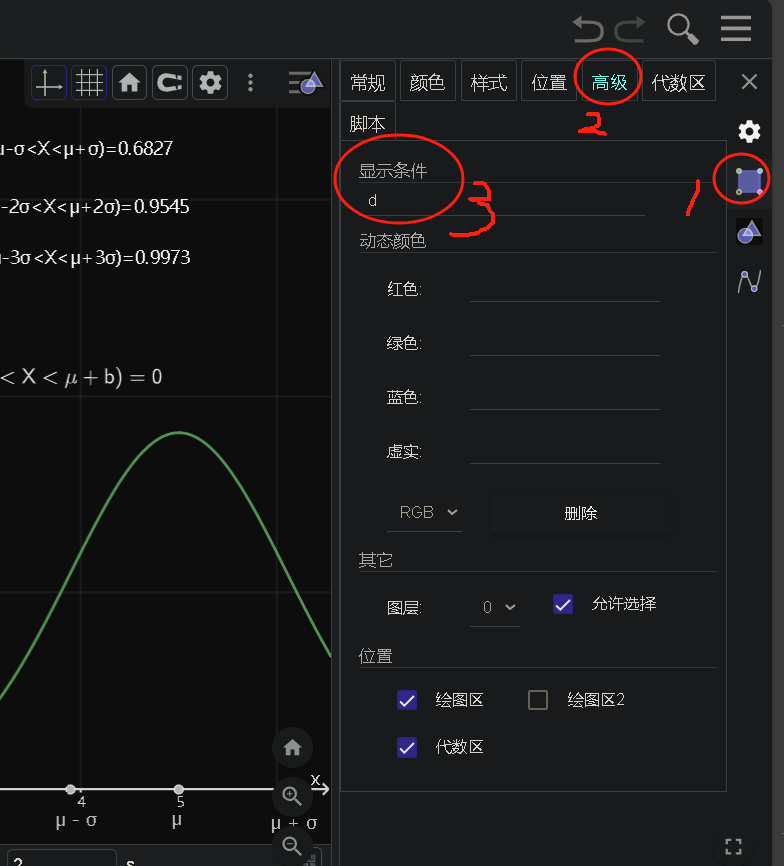
⑤我们右键修改复选框的标题，如下：

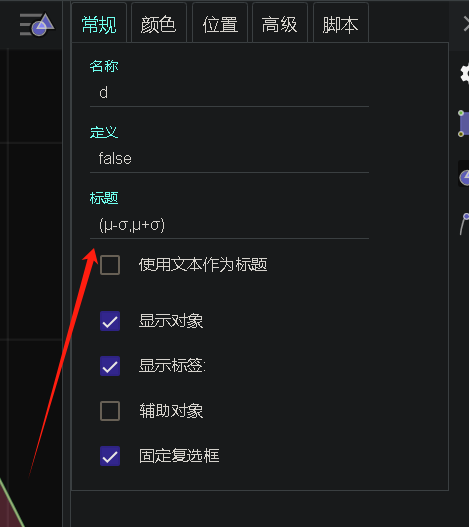
最终效果如下：

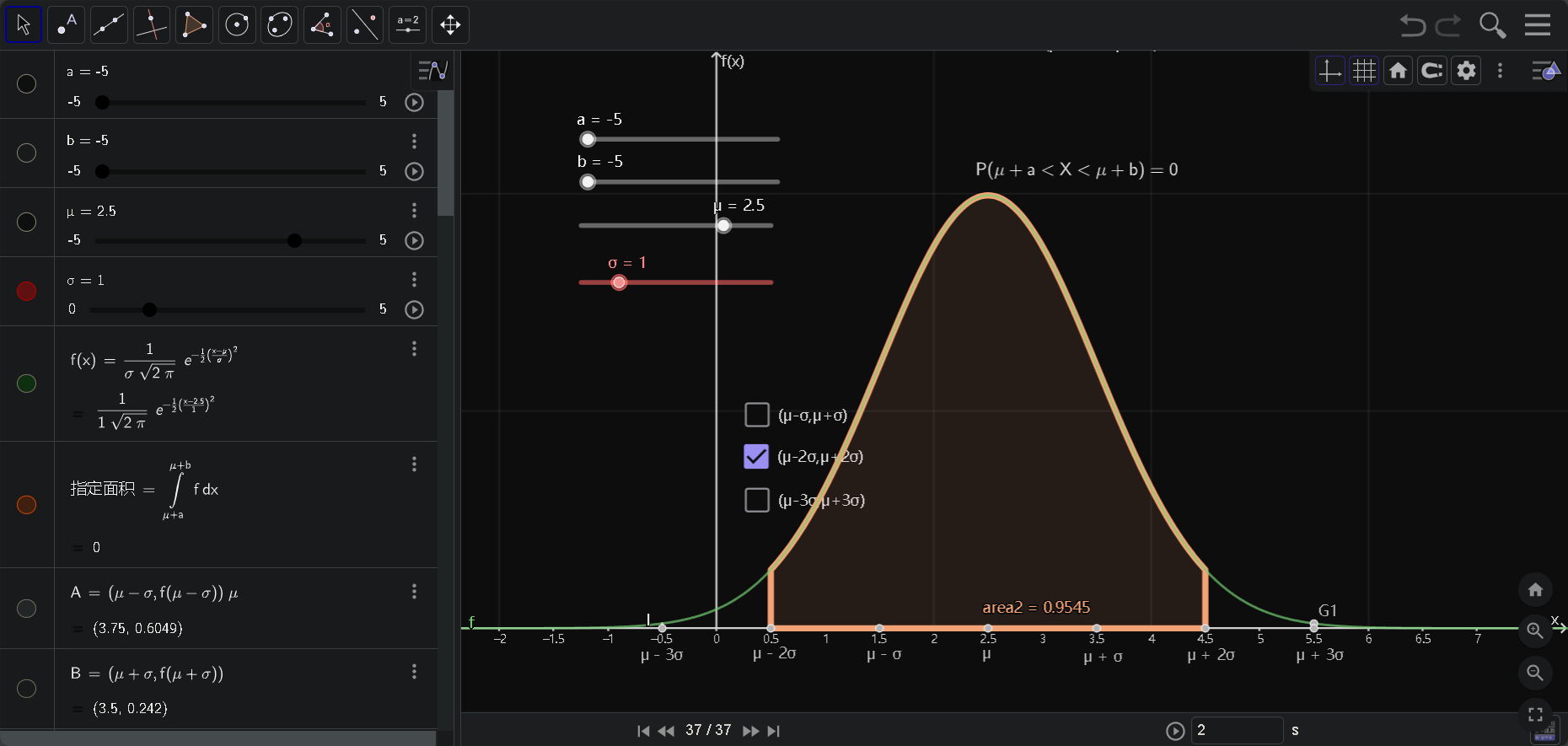
参考链接
https://www.geogebra.org/classic/m6hk9ndd

​