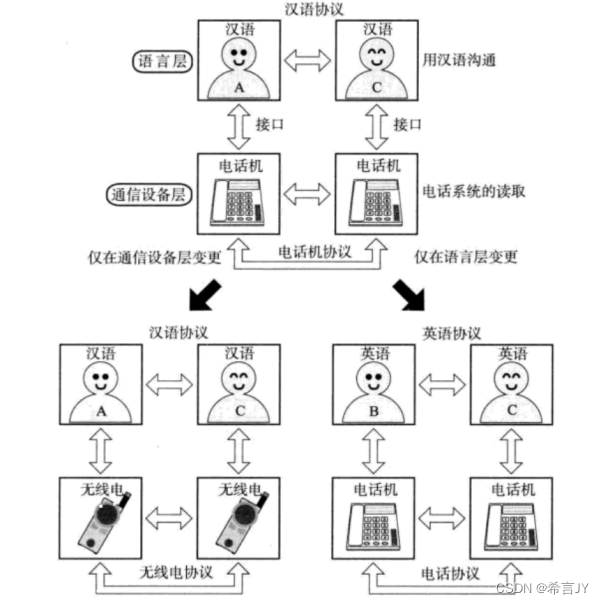
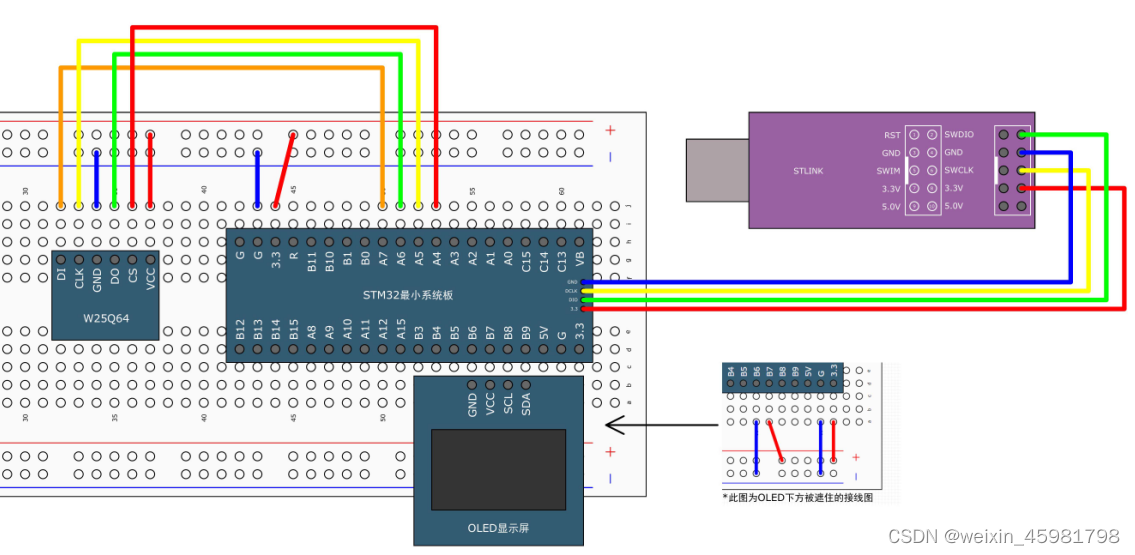
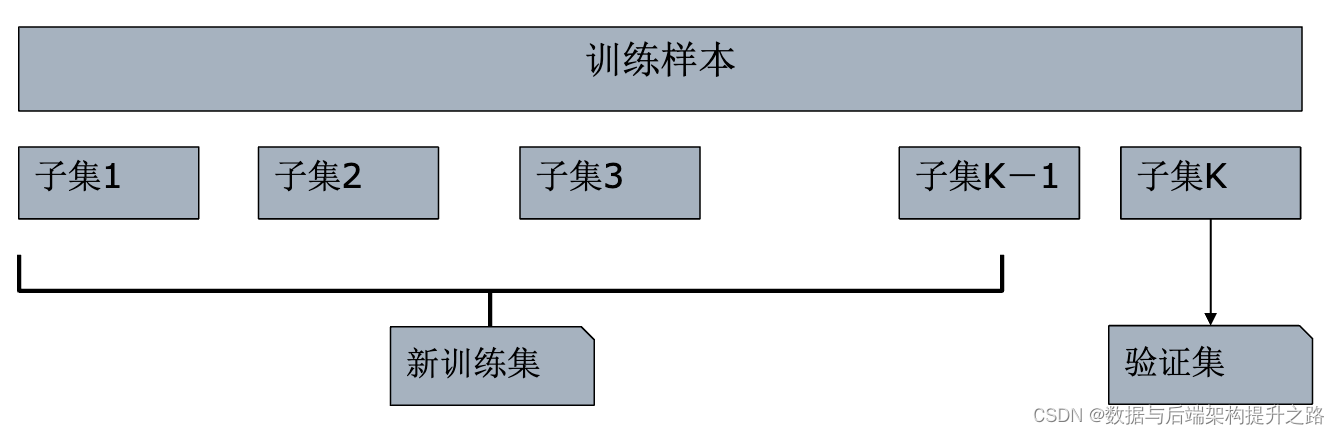
蓝桥杯真题讲解:
- 一、视频讲解
- 二、暴力代码
- 三、正解代码
一、视频讲解
视频讲解
二、暴力代码
//暴力代码:DFS
#include<bits/stdc++.h>
#define endl '\n'
#define deb(x) cout << #x << " = " << x << '\n';
#define INF 0x3f3f3f3f
#define int long long
using namespace std;
const int N = 2e5 + 10;
typedef pair<int,int> pii;
map<pii, int>st;//记录从{x, y}的距离是多少
int a[N];
vector<pii>edge[N];//存图
//s表示你要求的路径的起点
//v表示你要求的路径的终点
//u表示你当前走到了哪个点
//father表示你当前这个点的父亲节点是谁。避免重复走造成死循环
//sum表示从s走到u的路径花费总和。
bool dfs(int s, int u, int father, int v, int sum)
{
if(u == v)
{
st[{s, v}] = sum;
st[{v, s}] = sum;
// cout << s << " " << v << " " << sum << endl;
return true;
}
for(int i = 0; i < edge[u].size(); i ++)
{
int son = edge[u][i].first;
if(son == father)
continue;
int w = edge[u][i].second;
if(dfs(s, son, u, v, sum + w))
return true;
}
return false;
}
void solve()
{
int n, k;
cin >> n >> k;
for(int i = 0; i < n - 1; i ++)
{
int x, y, t;
cin >> x >> y >> t;
edge[x].push_back({y, t});
edge[y].push_back({x, t});
}
for(int i = 0; i < k; i ++)
cin >> a[i];
//求出完整路线的总花费
//O(k * n)
int ans = 0;
for(int i = 0; i < k - 1; i ++)
{
dfs(a[i], a[i], -1, a[i + 1], 0);
ans += st[{a[i] ,a[i + 1]}];
}
for(int i = 0; i < k; i ++)
{
int tmp = ans;
if(i == 0)
tmp -= st[{a[i], a[i + 1]}];
else if(i == k - 1)
tmp -= st[{a[i - 1], a[i]}];
else
{
tmp -= st[{a[i - 1], a[i]}];
tmp -= st[{a[i], a[i + 1]}];
dfs(a[i - 1], a[i - 1], -1, a[i + 1], 0);
tmp += st[{a[i - 1], a[i + 1]}];
}
cout << tmp << endl;
}
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int t = 1;
//cin >> t;
while(t--)
solve();
}
三、正解代码
//景区导游:树上前缀和 + 最近公共祖先
#include<bits/stdc++.h>
#define int long long
using namespace std;
typedef pair<int, int> pii;
const int N = 1e5 + 10;
int a[N], siz[N], dep[N], fa[N], son[N], top[N];
int sum[N];
int n, k;
vector<pii>edge[N];
void dfs1(int u, int father)
{
siz[u] = 1, dep[u] = dep[father] + 1;
fa[u] = father;
for(int i = 0; i < edge[u].size(); i ++)
{
int s = edge[u][i].first;
if(s == father)
continue;
dfs1(s, u);
siz[u] += siz[s];
if(siz[son[u]] < siz[s])
son[u] = s;
}
}
void dfs2(int u, int t)
{
top[u] = t;
if(son[u] == 0)
return;
dfs2(son[u], t);
for(int i = 0; i < edge[u].size(); i ++)
{
int s = edge[u][i].first;
if(s == son[u] || s == fa[u])
continue;
dfs2(s, s);
}
}
int lca(int u, int v)
{
while(top[u] != top[v])
{
if(dep[top[u]] < dep[top[v]])
swap(u, v);
u = fa[top[u]];
}
return dep[u] < dep[v] ? u : v;
}
void cal_sum(int u)
{
for(int i = 0; i < edge[u].size(); i ++)
{
int s = edge[u][i].first;
if(s == fa[u])
continue;
int w = edge[u][i].second;
sum[s] = sum[u] + w;
cal_sum(s);
}
}
void solve()
{
cin >> n >> k;
for(int i = 0; i < n - 1; i ++)
{
int x, y, t;
cin >> x >> y >> t;
edge[x].push_back({y, t});
edge[y].push_back({x, t});
}
for(int i = 1; i <= k; i ++)
cin >> a[i];
//树链剖分
dfs1(1, 0);
dfs2(1, 1);
//求树上的前缀和
cal_sum(1);
int ans = 0;
for(int i = 1; i <= k - 1; i ++)
{
int u = a[i], v = a[i + 1];
int cost = sum[u] + sum[v] - 2 * sum[lca(u, v)];
ans += cost;
}
for(int i = 1; i <= k; i ++)
{
int tmp = ans;
if(i == 1)
tmp -= sum[a[i + 1]] + sum[a[i]] - sum[lca(a[i], a[i + 1])] * 2;
else if(i == k)
tmp -= sum[a[i - 1]] + sum[a[i]] - sum[lca(a[i], a[i - 1])] * 2;
else
{
tmp -= sum[a[i + 1]] + sum[a[i]] - sum[lca(a[i], a[i + 1])] * 2;
tmp -= sum[a[i - 1]] + sum[a[i]] - sum[lca(a[i], a[i - 1])] * 2;
tmp += sum[a[i - 1]] + sum[a[i + 1]] - sum[lca(a[i + 1], a[i - 1])] * 2;
}
cout << tmp << " ";
}
cout << endl;
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0);
int t = 1;
while(t--)
solve();
}