104. 二叉树的最大深度
- 1、题目
- 2、题目分析
- 3、复杂度最优解代码示例
- 4、适用场景
1、题目
给定一个二叉树 root ,返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
示例 1:
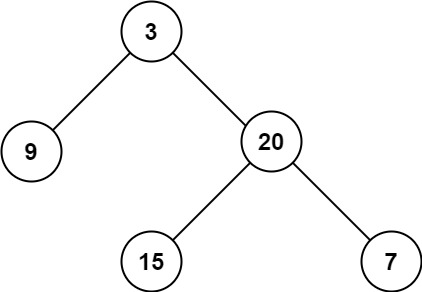
输入:root = [3,9,20,null,null,15,7] 输出:3
示例 2:
输入:root = [1,null,2] 输出:2
提示:
- 树中节点的数量在
[0, 104]区间内。 -100 <= Node.val <= 100
Related Topics
- 树
- 深度优先搜索
- 广度优先搜索
- 二叉树
2、题目分析
对每个节点都进行左右子树的深度搜索,有2个递归终止条件:①当前节点为null;②当前节点为叶子节点,此时要保存最大深度。
3、复杂度最优解代码示例
int maxDepth = 0;
public int maxDepth(TreeNode root) {
dfs(root, 1);
return maxDepth;
}
public void dfs(TreeNode node, int depth) {
if (node == null) {
// 踩坑:需要设置结束条件
return;
}
if (node.left == null && node.right == null) {
// 1.判断当前节点是否为叶子节点
maxDepth = Math.max(maxDepth, depth);
return;
}
// 2.往左子树、和右子树,深搜
dfs(node.left, depth + 1);
dfs(node.right, depth + 1);
}
4、适用场景
二叉树最大深度的计算在多个场景中都有广泛的应用,以下是一些具体的适用场景:
- 算法学习与教学:在计算机科学的学习和教学过程中,二叉树的最大深度是理解二叉树结构和树的遍历算法的基础。
- 数据结构设计:在设计需要快速检索的数据结构时,了解二叉树的深度有助于优化搜索算法的性能。
- 平衡性检查:对于平衡二叉树(如AVL树),最大深度的计算可以用来检查树的平衡性,确保树的操作效率。
- 树的遍历:在对二叉树进行遍历时,了解最大深度可以帮助确定遍历所需的时间和空间复杂度。
- 网络路由优化:在网络路由算法中,二叉树的最大深度可以用于评估和优化数据传输路径。
- 游戏开发:在游戏开发中,二叉树的最大深度可能用于构建游戏AI的决策树,以实现更复杂的决策逻辑。
- 机器学习:在机器学习领域,特别是在决策树算法中,最大深度的计算用于防止过拟合,通过剪枝来控制模型的复杂度。
- 文件系统管理:在文件系统中,二叉树的最大深度可以用于管理和优化文件的存储结构。