概述：配置graalvm或者用graalvm打包springboot项目请看下面文章：

Springboot3新特性：开发第一个 GraalVM 本机应用程序(完整教程)-CSDN博客

废话不多说，咱们开始用GraalVM打包maven项目。

第一步：引入依赖和插件

pom文件：

<?xml version="1.0" encoding="UTF-8"?>
<project xmlns="http://maven.apache.org/POM/4.0.0"
         xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance"
         xsi:schemaLocation="http://maven.apache.org/POM/4.0.0 http://maven.apache.org/xsd/maven-4.0.0.xsd">
    <modelVersion>4.0.0</modelVersion>

    <groupId>org.example</groupId>
    <artifactId>HelloWorldNative</artifactId>
    <version>1.0-SNAPSHOT</version>

    <properties>
        <maven.compiler.source>17</maven.compiler.source>
        <maven.compiler.target>17</maven.compiler.target>
        <project.build.sourceEncoding>UTF-8</project.build.sourceEncoding>
        <java.version>17</java.version>
        <project.build.sourceEncoding>UTF-8</project.build.sourceEncoding>
        <project.reporting.outputEncoding>UTF-8</project.reporting.outputEncoding>
        <spring-boot.version>3.2.1</spring-boot.version>
        <graalvm.version>21.2.0</graalvm.version>
    </properties>

    <dependencies>
        <dependency>
            <groupId>org.graalvm.sdk</groupId>
            <artifactId>graal-sdk</artifactId>
            <version>${graalvm.version}</version>
            <scope>provided</scope>
        </dependency>
    </dependencies>

    <build>
        <plugins>
            <plugin>
                <groupId>org.graalvm.nativeimage</groupId>
                <artifactId>native-image-maven-plugin</artifactId>
                <version>${graalvm.version}</version>
                <executions>
                    <execution>
                        <goals>
                            <goal>native-image</goal>
                        </goals>
                        <phase>package</phase>
                    </execution>
                </executions>
                <configuration>
                    <skip>false</skip>
                    <imageName>main</imageName>
                    <mainClass>org.example.Main</mainClass>
                    <buildArgs>
                        --no-fallback
                    </buildArgs>
                </configuration>
            </plugin>
        </plugins>
    </build>


</project>

第二步：编写代码

package org.example;

public class Main {

    public static void main(String[] args) {
        System.out.println("Hello world!");

    }
}

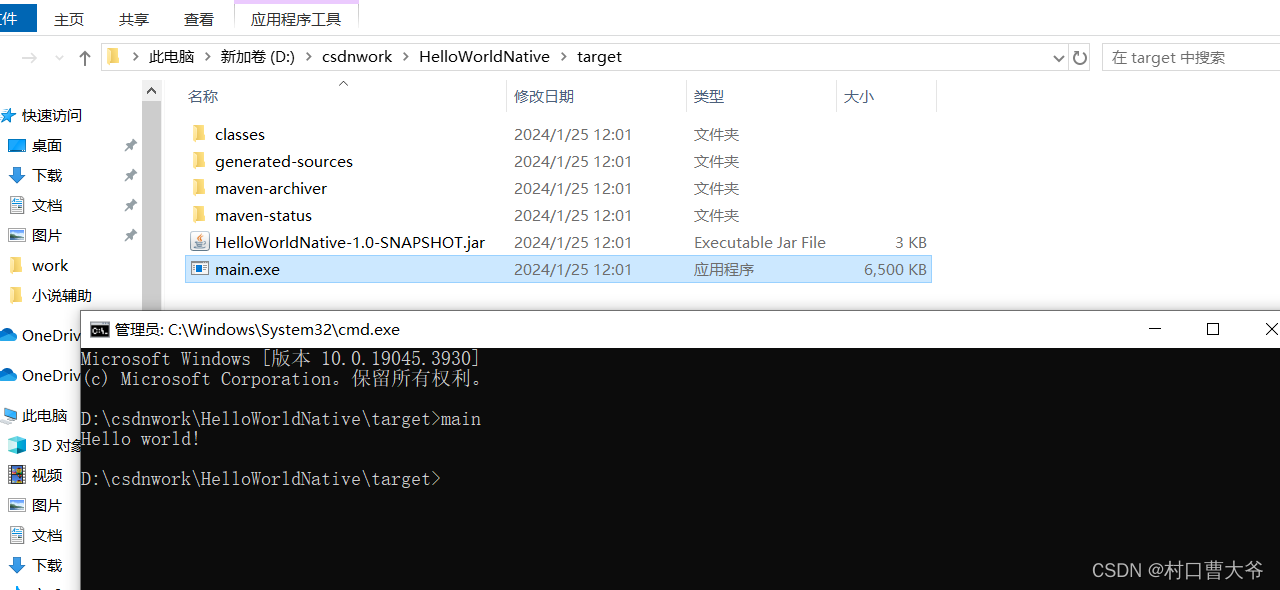
第三步：打包maven

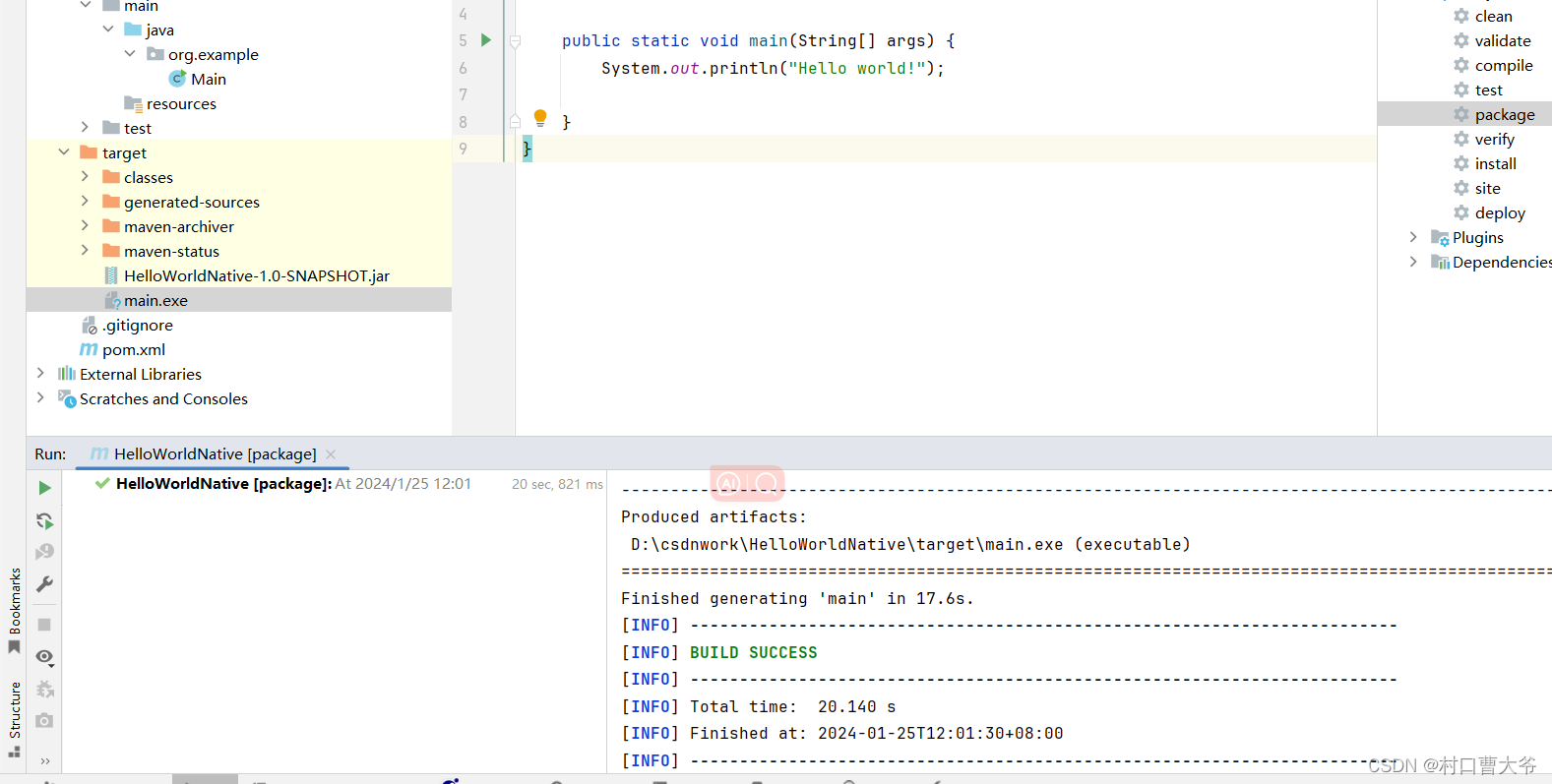
第四步：运行查看结果