目录

738.单调递增的数字 

💡解题思路

💻实现代码

968.监控二叉树 

💡解题思路

确定遍历顺序

如何隔两个节点放一个摄像头

💻实现代码

总结

---

738.单调递增的数字 

题目链接：738.单调递增的数字

给定一个非负整数 N，找出小于或等于 N 的最大的整数，同时这个整数需要满足其各个位数上的数字是单调递增。

（当且仅当每个相邻位数上的数字 x 和 y 满足 x <= y 时，我们称这个整数是单调递增的。）

示例 1:

• 输入: N = 10
• 输出: 9

示例 2:

• 输入: N = 1234
• 输出: 1234

示例 3:

• 输入: N = 332
• 输出: 299

说明: N 是在 [0, 10^9] 范围内的一个整数。

💡解题思路

题目要求小于等于N的最大单调递增的整数，那么拿一个两位的数字来举例。

例如：98，一旦出现strNum[i - 1] > strNum[i]的情况（非单调递增），首先想让strNum[i - 1]--，然后strNum[i]给为9，这样这个整数就是89，即小于98的最大的单调递增整数。

这一点如果想清楚了，这道题就好办了。

此时是从前向后遍历还是从后向前遍历呢？

从前向后遍历的话，遇到strNum[i - 1] > strNum[i]的情况，让strNum[i - 1]减一，但此时如果strNum[i - 1]减一了，可能又小于strNum[i - 2]。

这么说有点抽象，举个例子，数字：332，从前向后遍历的话，那么就把变成了329，此时2又小于了第一位的3了，真正的结果应该是299。

那么从后向前遍历，就可以重复利用上次比较得出的结果了，从后向前遍历332的数值变化为：332 -> 329 -> 299

确定了遍历顺序之后，那么此时局部最优就可以推出全局，找不出反例，试试贪心。

💻实现代码

class Solution {
    public int monotoneIncreasingDigits(int n) {
        String s=String.valueOf(n);
        char[] ch=s.toCharArray();
        int len=s.length();
        int start=s.length();
        for(int i=len-2;i>=0;i--){
            if(ch[i]>ch[i+1]){
                ch[i]--;
                start=i+1;
            }
        }
        for(int i=start;i<len;i++){
            ch[i]='9';
        }
        return Integer.parseInt(String.valueOf(ch));

    }
}

968.监控二叉树 

题目链接：968.监控二叉树

给定一个二叉树，我们在树的节点上安装摄像头。

节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。

计算监控树的所有节点所需的最小摄像头数量。

示例 1：

• 输入：[0,0,null,0,0]
• 输出：1
• 解释：如图所示，一台摄像头足以监控所有节点。

示例 2：

• 输入：[0,0,null,0,null,0,null,null,0]
• 输出：2
• 解释：需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。

提示：

• 给定树的节点数的范围是 [1, 1000]。
• 每个节点的值都是 0。

💡解题思路

这道题目首先要想，如何放置，才能让摄像头最小的呢？

从题目中示例，其实可以得到启发，我们发现题目示例中的摄像头都没有放在叶子节点上！

这是很重要的一个线索，摄像头可以覆盖上中下三层，如果把摄像头放在叶子节点上，就浪费的一层的覆盖。

所以把摄像头放在叶子节点的父节点位置，才能充分利用摄像头的覆盖面积。

那么有同学可能问了，为什么不从头结点开始看起呢，为啥要从叶子节点看呢？

因为头结点放不放摄像头也就省下一个摄像头， 叶子节点放不放摄像头省下了的摄像头数量是指数阶别的。

所以我们要从下往上看，局部最优：让叶子节点的父节点安摄像头，所用摄像头最少，整体最优：全部摄像头数量所用最少！

局部最优推出全局最优，找不出反例，那么就按照贪心来！

此时，大体思路就是从低到上，先给叶子节点父节点放个摄像头，然后隔两个节点放一个摄像头，直至到二叉树头结点。

此时这道题目还有两个难点：

1. 二叉树的遍历
2. 如何隔两个节点放一个摄像头

确定遍历顺序

在二叉树中如何从低向上推导呢？

可以使用后序遍历也就是左右中的顺序，这样就可以在回溯的过程中从下到上进行推导了。

如何隔两个节点放一个摄像头

此时需要状态转移的公式，大家不要和动态的状态转移公式混到一起，本题状态转移没有择优的过程，就是单纯的状态转移！

来看看这个状态应该如何转移，先来看看每个节点可能有几种状态：

有如下三种：

• 该节点无覆盖
• 本节点有摄像头
• 本节点有覆盖

我们分别有三个数字来表示：

• 0：该节点无覆盖
• 1：本节点有摄像头
• 2：本节点有覆盖

大家应该找不出第四个节点的状态了。

一些同学可能会想有没有第四种状态：本节点无摄像头，其实无摄像头就是 无覆盖 或者 有覆盖的状态，所以一共还是三个状态。

因为在遍历树的过程中，就会遇到空节点，那么问题来了，空节点究竟是哪一种状态呢？ 空节点表示无覆盖？ 表示有摄像头？还是有覆盖呢？

回归本质，为了让摄像头数量最少，我们要尽量让叶子节点的父节点安装摄像头，这样才能摄像头的数量最少。

那么空节点不能是无覆盖的状态，这样叶子节点就要放摄像头了，空节点也不能是有摄像头的状态，这样叶子节点的父节点就没有必要放摄像头了，而是可以把摄像头放在叶子节点的爷爷节点上。

所以空节点的状态只能是有覆盖，这样就可以在叶子节点的父节点放摄像头了

接下来就是递推关系。

那么递归的终止条件应该是遇到了空节点，此时应该返回2（有覆盖），原因上面已经解释过了。

代码如下：

// 空节点，该节点有覆盖
if (cur == NULL) return 2;

递归的函数，以及终止条件已经确定了，再来看单层逻辑处理。

主要有如下四类情况：

• 情况1：左右节点都有覆盖

左孩子有覆盖，右孩子有覆盖，那么此时中间节点应该就是无覆盖的状态了。

如图：

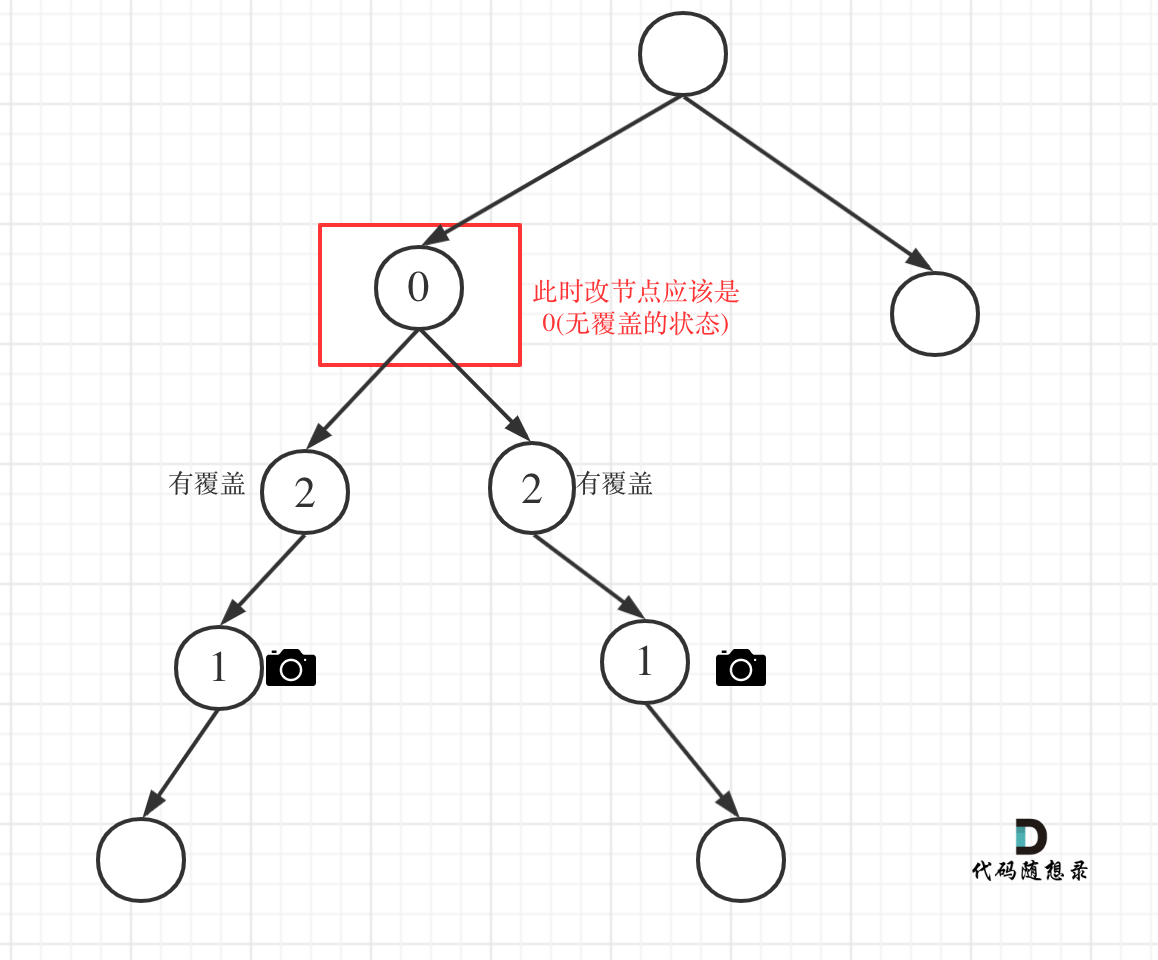
代码如下：

// 左右节点都有覆盖
if (left == 2 && right == 2) return 0;

• 情况2：左右节点至少有一个无覆盖的情况

如果是以下情况，则中间节点（父节点）应该放摄像头：

• left == 0 && right == 0 左右节点无覆盖
• left == 1 && right == 0 左节点有摄像头，右节点无覆盖
• left == 0 && right == 1 左节点有无覆盖，右节点摄像头
• left == 0 && right == 2 左节点无覆盖，右节点覆盖
• left == 2 && right == 0 左节点覆盖，右节点无覆盖

这个不难理解，毕竟有一个孩子没有覆盖，父节点就应该放摄像头。

此时摄像头的数量要加一，并且return 1，代表中间节点放摄像头。

代码如下：

if (left == 0 || right == 0) {
    result++;
    return 1;
}

• 情况3：左右节点至少有一个有摄像头

如果是以下情况，其实就是 左右孩子节点有一个有摄像头了，那么其父节点就应该是2（覆盖的状态）

• left == 1 && right == 2 左节点有摄像头，右节点有覆盖
• left == 2 && right == 1 左节点有覆盖，右节点有摄像头
• left == 1 && right == 1 左右节点都有摄像头

代码如下：

if (left == 1 || right == 1) return 2;

从这个代码中，可以看出，如果left == 1, right == 0 怎么办？其实这种条件在情况2中已经判断过了，如图：

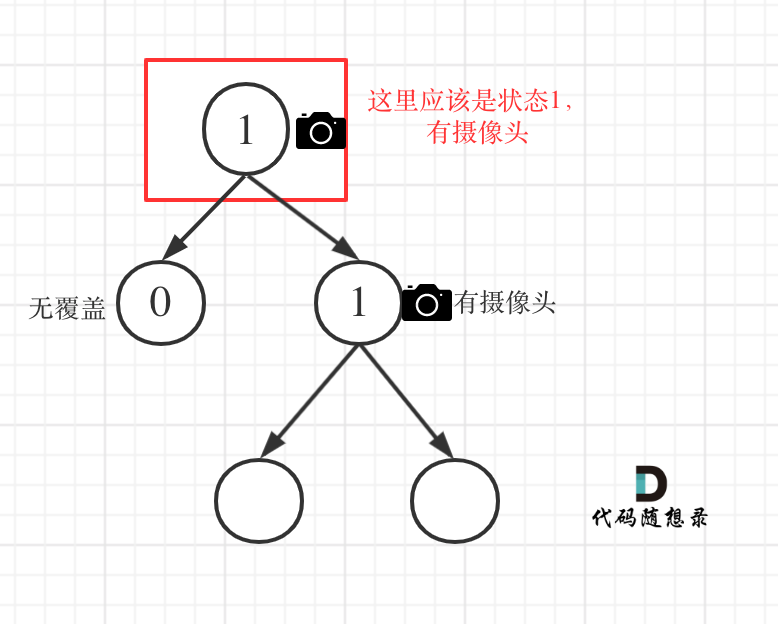
这种情况也是大多数同学容易迷惑的情况。

1. 情况4：头结点没有覆盖

以上都处理完了，递归结束之后，可能头结点 还有一个无覆盖的情况，如图：

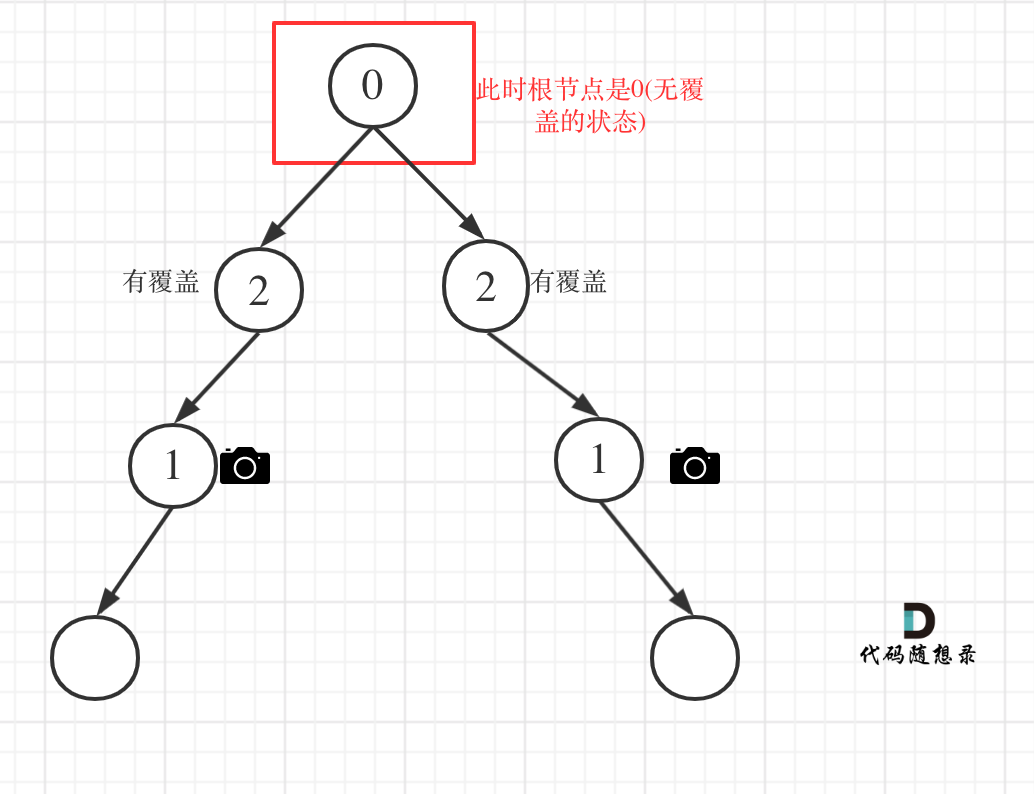
所以递归结束之后，还要判断根节点，如果没有覆盖，result++，代码如下：

int minCameraCover(TreeNode* root) {
    result = 0;
    if (traversal(root) == 0) { // root 无覆盖
        result++;
    }
    return result;
}

💻实现代码

class Solution {
    int  res=0;
    public int minCameraCover(TreeNode root) {
        // 对根节点的状态做检验,防止根节点是无覆盖状态 .
        if(minCame(root)==0){
            res++;
        }
        return res;
    }
    /**
     节点的状态值：
       0 表示无覆盖
       1 表示 有摄像头
       2 表示有覆盖
    后序遍历，根据左右节点的情况,来判读 自己的状态
     */
    public int minCame(TreeNode root){
        if(root==null){
            // 空节点默认为 有覆盖状态，避免在叶子节点上放摄像头
            return 2;
        }
        int left=minCame(root.left);
        int  right=minCame(root.right);

        // 如果左右节点都覆盖了的话, 那么本节点的状态就应该是无覆盖,没有摄像头
        if(left==2&&right==2){
            //(2,2)
            return 0;
        }else if(left==0||right==0){
            // 左右节点都是无覆盖状态,那 根节点此时应该放一个摄像头
            // (0,0) (0,1) (0,2) (1,0) (2,0)
            // 状态值为 1 摄像头数 ++;
            res++;
            return 1;
        }else{
            // 左右节点的 状态为 (1,1) (1,2) (2,1) 也就是左右节点至少存在 1个摄像头，
            // 那么本节点就是处于被覆盖状态
            return 2;
        }
    }
}

总结