文章目录
- 支持向量机
- 1. 间隔与支持向量
- 1.1. 点到超平面的距离
- 1.2. 去掉绝对值
- 1.3. 最大间隔
- 2. 对偶问题
- 3. 核函数
- 3.1. 使用核函数的原因
- 3.2. 特征空间变换
- 3.3. 空间内积转化为核函数
- 3.4. 常用核函数
- 4. 软间隔与正则化
- 4.1. 软间隔
- 4.2. 松弛变量
- 4.3. 替代损失函数
- 4.4. 修改拉格朗日乘子
- 5. SVM具体实现
- 5.1. 最大边际分隔超平面
- 5.1.1. 具体实现一
- 5.1.2. 具体实现二
- 5.2. 非线性支持向量机
- 5.2.1. 具体实现一
- 5.2.2. 具体实现二
- 5.3. 软间隔
- 6. 高斯核函数
- 6.1. 特征变换
- 6.2. 算法模拟
- 6.3. 对比分析
支持向量机
支持向量机(SVM)是一种有监督的二分类模型, 分为线性和非线性两大类, 主要思想是在空间中找到一个能够将所有数据样本划开的超平面,并且使得样本集中所有数据到这个超平面的距离最远。
优点:
- 在高维空间里也非常有效;
- 对于数据维度远高于数据样本量的情况也有效;
- 在决策函数中使用训练集的子集(也称为支持向量),因此也是内存高效利用的;
- 很强的通用性,可以为决策函数指定不同的核函数,已经提供的通用核函数和自定义核函数。
缺点:
- 如果特征数量远远大于样本数,则在选择核函数和正则化项时要避免过度拟合;
- SVM不直接提供概率估计。
分类: SVC、NuSVC、LinearSVC
1. 间隔与支持向量
分类学习的基本思想就是基于训练集D在样本空间中找到一个划分超平面,将不同的样本分开。如下图所示,一共有五个超平面可以把训练集分开,如何去选择一个合适的超平面至关重要。在下图中我们称红色的超平面为最好的超平面,因为这个红色的划分超平面所产生的分类结果是最鲁棒性的,对未见示例的泛化能力最强。

寻找最大间隔,如下图右侧子图所示,离数据集构成的超平面距离最大时,此间的距离就是支持向量,说成支撑向量更容易理解一点。

1.1. 点到超平面的距离

如上图所示,寻找平面外一点x到平面的距离,基本的思路就是在平面上找两个点X'与X",连接X'和X",构成线段,找出线段的垂线使垂线垂直于平面,此时w就是平面的法向量,求x到X'的距离,然后把距离投影到法向量方向即可得到dist(x,h)。
设划分超平面的方程为:
w
T
x
+
b
=
0
w^Tx+b=0
wTx+b=0,X'与X"在平面上,满足平面方程,带入后得到:
{ w T X ′ + b = 0 w T X ′ ′ + b = 0 → { w T X ′ = − b w T X ′ ′ = − b \begin{cases} w^TX'+b=0 \\ w^TX''+b=0 \end{cases} \rightarrow \begin{cases} w^TX'=-b \\ w^TX''=-b \end{cases} {wTX′+b=0wTX′′+b=0→{wTX′=−bwTX′′=−b
可以得到:
d
i
s
t
(
x
,
b
,
w
)
=
∣
w
T
∣
∣
w
∣
∣
∣
(
x
−
X
′
)
=
∣
w
T
x
+
b
∣
∣
∣
w
∣
∣
dist(x,b,w)=| \frac{w^T}{||w||} |(x-X') = \frac{|w^Tx+b|}{||w||}
dist(x,b,w)=∣∣∣w∣∣wT∣(x−X′)=∣∣w∣∣∣wTx+b∣
其中
w
=
(
w
1
;
w
2
;
…
;
w
d
)
w=(w_1;w_2;…;w_d)
w=(w1;w2;…;wd)为法向量,决定了超平面的方向;b为位移项,决定了超平面与原点之间的距离。显然,超平面可由w和b决定。
1.2. 去掉绝对值
假设超平面能将样本正确分类,若
y
i
=
+
1
y_i=+1
yi=+1,则有
w
T
x
i
+
b
>
0
w^Tx_i+b>0
wTxi+b>0;若
y
i
=
−
1
y_i=-1
yi=−1,则有
w
T
x
i
+
b
>
0
w^Tx_i+b>0
wTxi+b>0,即
{
w
T
x
i
+
b
≥
+
1
,
y
i
=
+
1
w
T
x
i
+
b
≤
−
1
,
y
i
=
−
1
\begin{cases} w^Tx_i+b\geq+1, \quad\quad y_i=+1 \\ w^Tx_i+b\leq-1,\quad \quad y_i=-1 \end{cases}
{wTxi+b≥+1,yi=+1wTxi+b≤−1,yi=−1
去掉绝对值后,点到直线的距离可以表示为:
d
i
s
t
=
y
i
⋅
(
w
T
x
i
+
b
)
∣
∣
w
∣
∣
dist = \frac{y_i\cdot(w^Tx_i+b)}{||w||}
dist=∣∣w∣∣yi⋅(wTxi+b)
如下图所示,距离超平面最近的几个点可以使上式成立,那么这几个点称为支持向量,两个支持向量到超平面的距离之和为:
γ
=
2
∣
∣
w
∣
∣
\gamma = \frac{2}{||w||}
γ=∣∣w∣∣2,此式也称为间隔。

1.3. 最大间隔
要想找到最大间隔,就是让间隔的公式取最大值,即:
m
a
x
γ
=
m
a
x
w
,
b
2
∣
∣
w
∣
∣
当
y
i
⋅
(
w
T
x
i
+
b
)
≥
1
,
i
=
1
,
2
,
…
,
m
.
(
1.1
)
max \gamma = max_{w,b}\quad\frac{2}{||w||}\quad 当y_i\cdot(w^Tx_i+b)\geq1,i=1,2,…,m.\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad(1.1)
maxγ=maxw,b∣∣w∣∣2当yi⋅(wTxi+b)≥1,i=1,2,…,m.(1.1)
为了最大化间隔,仅需最大化
∣
∣
w
∣
∣
−
1
||w||^{-1}
∣∣w∣∣−1,这就等价于最小化
∣
∣
w
∣
∣
2
||w||^{2}
∣∣w∣∣2,于是距离公式就变成:
m
a
x
γ
=
m
i
n
w
,
b
1
2
∣
∣
w
∣
∣
2
当
y
i
⋅
(
w
T
x
i
+
b
)
≥
1
,
i
=
1
,
2
,
…
,
m
.
(
1.2
)
max \gamma = min_{w,b}\quad\frac{1}{2}||w||^{2}\quad 当y_i\cdot(w^Tx_i+b)\geq1,i=1,2,…,m.\quad\quad\quad\quad\quad\quad\quad\quad\quad (1.2)
maxγ=minw,b21∣∣w∣∣2当yi⋅(wTxi+b)≥1,i=1,2,…,m.(1.2)
这就是支持向量机的基本型。
2. 对偶问题
2.1. 引入拉格朗日乘子
对公式(3.2)的每条约束条件添加拉格朗日乘子:
α
i
≥
0
\alpha _i \geq 0
αi≥0,则该问题的拉格朗日函数可以写为:
L
(
w
,
b
,
α
)
=
1
2
∣
∣
w
∣
∣
2
+
∑
i
=
1
m
α
i
(
1
−
y
i
(
w
T
x
i
+
b
)
)
(
2.1
)
L(w,b,\alpha)=\frac{1}{2}||w||^2 + \sum_{i=1}^{m}{\alpha_i}(1-y_i(w^Tx_i+b)) \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad (2.1)
L(w,b,α)=21∣∣w∣∣2+i=1∑mαi(1−yi(wTxi+b))(2.1)
其中
α
=
(
α
1
;
α
2
;
…
;
α
m
)
\alpha=(\alpha_1;\alpha_2;…;\alpha_m)
α=(α1;α2;…;αm)
2.2. 求偏导
令 L ( w , b , α ) L(w,b,\alpha) L(w,b,α) 对 w w w 和 b 求偏导且让其偏导为零可得到:
w = ∑ i = 1 m α i y i x i ( 2.2 ) 0 = ∑ i = 1 m α i y i ( 2.3 ) w=\sum_{i=1}^{m}{\alpha_iy_ix_i} \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad (2.2) \\ 0=\sum_{i=1}^{m}{\alpha_iy_i} \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad (2.3) w=i=1∑mαiyixi(2.2)0=i=1∑mαiyi(2.3)
2.3. 得到对偶问题
结合对偶问题应用到我们的求解中就是如下的转换:
m
i
n
w
,
b
m
a
x
α
L
(
w
,
b
,
α
)
−
>
m
a
x
α
m
i
n
w
,
b
L
(
w
,
b
,
α
)
min_{w,b}max _\alpha L(w,b,\alpha) -> max _\alpha min_{w,b} L(w,b,\alpha)
minw,bmaxαL(w,b,α)−>maxαminw,bL(w,b,α)
2.4. 求解内层函数 m i n w , b L ( w , b , α ) min_{w,b} L(w,b,\alpha) minw,bL(w,b,α)
下面先来求解 m i n w , b L ( w , b , α ) min_{w,b} L(w,b,\alpha) minw,bL(w,b,α):
把 (2.2) 与 (2.3) 带入到 (2.1) ,消去
L
(
w
,
b
,
α
)
L(w,b,\alpha)
L(w,b,α) 的
w
w
w和b:
m
i
n
w
,
b
L
(
w
,
b
,
α
)
=
1
2
∣
∣
w
∣
∣
2
+
∑
i
=
1
m
α
i
(
1
−
y
i
(
w
T
x
i
+
b
)
)
=
1
2
w
T
w
−
w
T
∑
i
=
1
m
α
i
y
i
x
i
−
b
∑
i
=
1
m
α
i
y
i
+
∑
i
=
1
m
α
i
=
∑
i
=
1
m
α
i
−
1
2
(
∑
i
=
1
m
α
i
y
i
x
i
)
T
∑
i
=
1
m
α
i
y
i
x
i
=
∑
i
=
1
m
α
i
−
1
2
∑
i
=
1
m
∑
j
=
1
m
α
i
α
j
y
i
y
j
x
i
T
x
j
min_{w,b}L(w,b,\alpha)=\frac{1}{2}||w||^2 + \sum_{i=1}^{m}{\alpha_i}(1-y_i(w^Tx_i+b)) \\ =\frac{1}{2}w^Tw-w^T \sum_{i=1}^{m}\alpha_iy_ix_i-b\sum_{i=1}^{m}\alpha_iy_i+\sum_{i=1}^{m}\alpha_i \quad\quad\quad\\ =\sum_{i=1}^{m}\alpha_i-\frac{1}{2}(\sum_{i=1}^{m}\alpha_iy_ix_i)^T\sum_{i=1}^{m}\alpha_iy_ix_i \quad\quad\quad\quad\quad\quad\quad\\ =\sum_{i=1}^{m}{\alpha_i} - \frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_i\alpha_jy_iy_jx_i^Tx_j\quad\quad\quad\quad\quad\quad\quad\quad
minw,bL(w,b,α)=21∣∣w∣∣2+i=1∑mαi(1−yi(wTxi+b))=21wTw−wTi=1∑mαiyixi−bi=1∑mαiyi+i=1∑mαi=i=1∑mαi−21(i=1∑mαiyixi)Ti=1∑mαiyixi=i=1∑mαi−21i=1∑mj=1∑mαiαjyiyjxiTxj
即可得到如下对偶问题,此时也完成了第一步求解
m
i
n
w
,
b
L
(
w
,
b
,
α
)
min_{w,b} L(w,b,\alpha)
minw,bL(w,b,α):
m
a
x
α
∑
i
=
1
m
α
i
−
1
2
∑
i
=
1
m
∑
j
=
1
m
α
i
α
j
y
i
y
j
x
i
T
x
j
条
件
{
∑
i
=
1
m
α
i
y
i
=
0
α
i
≥
0
,
i
=
1
,
2
,
…
,
m
.
(
2.4
)
max _\alpha \quad \sum_{i=1}^{m}{\alpha_i} - \frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_i\alpha_jy_iy_jx_i^Tx_j \quad\quad\quad 条件\begin{cases} \sum_{i=1}^{m}{\alpha_iy_i}=0 \\ \alpha _i \geq 0,\quad i=1,2,…,m. \end{cases} \quad (2.4)
maxαi=1∑mαi−21i=1∑mj=1∑mαiαjyiyjxiTxj条件{∑i=1mαiyi=0αi≥0,i=1,2,…,m.(2.4)
该对偶问题的KKT条件为:
{
α
i
≥
0
;
y
i
f
(
x
i
)
−
1
≥
0
;
α
i
(
y
i
f
(
x
i
)
−
1
)
=
0.
\begin{cases} \alpha _i \geq 0; \\y_if(x_i) - 1 \geq 0; \\ \alpha _i(y_if(x_i) - 1) = 0. \end{cases}
⎩⎪⎨⎪⎧αi≥0;yif(xi)−1≥0;αi(yif(xi)−1)=0.
于是对任意的训练样本
(
x
i
,
y
i
)
(x_i,y_i)
(xi,yi),总有
α
i
=
0
\alpha _i = 0
αi=0 或
y
i
f
(
x
i
)
=
1
y_if(x_i) = 1
yif(xi)=1 。若
α
i
=
0
\alpha _i = 0
αi=0 ,不会对样本产生影响;若
α
i
>
0
\alpha _i >0
αi>0 , 则必有
y
i
f
(
x
i
)
=
1
y_if(x_i) = 1
yif(xi)=1 ,所对应的样本点位于最大间隔边界上,是一个支持向量,这显示出支持向量机的一个重 要性质:训练完成后,大部分的训练样本都不需要保留,最终模型仅与支持向量有关。
2.5. 求解外层函数 m a x α m i n w , b L ( w , b , α ) max _\alpha min_{w,b} L(w,b,\alpha) maxαminw,bL(w,b,α)
继续对
α
\alpha
α 求极大值:
m
a
x
α
∑
i
=
1
m
α
i
−
1
2
∑
i
=
1
m
∑
j
=
1
m
α
i
α
j
y
i
y
j
x
i
T
x
j
条
件
{
∑
i
=
1
m
α
i
y
i
=
0
α
i
≥
0
,
i
=
1
,
2
,
…
,
m
.
max _\alpha \quad \sum_{i=1}^{m}{\alpha_i} - \frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_i\alpha_jy_iy_jx_i^Tx_j \quad\quad\quad 条件\begin{cases} \sum_{i=1}^{m}{\alpha_iy_i}=0 \\ \alpha _i \geq 0,\quad i=1,2,…,m. \end{cases}
maxαi=1∑mαi−21i=1∑mj=1∑mαiαjyiyjxiTxj条件{∑i=1mαiyi=0αi≥0,i=1,2,…,m.
极大值转换成求极小值:
m
i
n
α
1
2
∑
i
=
1
m
∑
j
=
1
m
α
i
α
j
y
i
y
j
x
i
T
x
j
−
∑
i
=
1
m
α
i
条
件
{
∑
i
=
1
m
α
i
y
i
=
0
α
i
≥
0
,
i
=
1
,
2
,
…
,
m
.
min _\alpha \quad \frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_i\alpha_jy_iy_jx_i^Tx_j-\sum_{i=1}^{m}{\alpha_i} \quad\quad\quad 条件\begin{cases} \sum_{i=1}^{m}{\alpha_iy_i}=0 \\ \alpha _i \geq 0,\quad i=1,2,…,m. \end{cases}
minα21i=1∑mj=1∑mαiαjyiyjxiTxj−i=1∑mαi条件{∑i=1mαiyi=0αi≥0,i=1,2,…,m.
求出的最终模型为:
f
(
x
)
=
w
T
x
+
b
=
∑
i
=
1
m
α
i
y
i
x
i
T
x
+
b
f(x) =w^Tx+b\\ \quad\quad\quad\quad\quad =\sum_{i=1}^{m}{\alpha_iy_ix_i^Tx + b}
f(x)=wTx+b=i=1∑mαiyixiTx+b
3. 核函数
3.1. 使用核函数的原因
之前的讨论中,训练样本都是线性可分的,即存在一个超平面能将训练样本正确分类,然而现实任务中,原始样本空间也许并不存在一个超平面 能够将训练样本集分开,如下图所示的样本集。我们需要将样本原始空间映射到一个更高维的特征空间,使得样本在这个空间内线性可分。理论上,如果原始空间维数有限,那么一定存在一个高维特征空间使样本可分。

3.2. 特征空间变换
下面要做
x
−
>
ϕ
(
x
)
x-> \phi (x)
x−>ϕ(x) 的映射,那么在高维空间中划分超平面对应的模型科表示为:
f
(
x
)
=
w
T
ϕ
(
x
)
+
b
f(x) =w^T \phi (x)+b
f(x)=wTϕ(x)+b
在特征空间中,其对应的对偶问题是:
m
a
x
α
∑
i
=
1
m
α
i
−
1
2
∑
i
=
1
m
∑
j
=
1
m
α
i
α
j
y
i
y
j
ϕ
(
x
i
)
T
ϕ
(
x
j
)
条
件
{
∑
i
=
1
m
α
i
y
i
=
0
α
i
≥
0
,
i
=
1
,
2
,
…
,
m
.
(
3.1
)
max _\alpha \quad \sum_{i=1}^{m}{\alpha_i} - \frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_i\alpha_jy_iy_j\phi (x_i)^T\phi (x_j) \quad\quad\quad 条件\begin{cases} \sum_{i=1}^{m}{\alpha_iy_i}=0 \\ \alpha _i \geq 0,\quad i=1,2,…,m. \end{cases} \quad\quad \quad(3.1)
maxαi=1∑mαi−21i=1∑mj=1∑mαiαjyiyjϕ(xi)Tϕ(xj)条件{∑i=1mαiyi=0αi≥0,i=1,2,…,m.(3.1)
3.3. 空间内积转化为核函数
设
κ
(
x
i
,
x
j
)
=
ϕ
(
x
i
)
T
ϕ
(
x
j
)
\kappa (x_i,x_j)= \phi (x_i)^T\phi (x_j)
κ(xi,xj)=ϕ(xi)Tϕ(xj) ,即
x
i
x_i
xi与
x
j
x_j
xj在特征空间的内积等于它们在原始样本空间中通过函数
κ
(
⋅
,
⋅
)
\kappa ( \cdot , \cdot )
κ(⋅,⋅) 计算的结果。于是 (3.1) 式可重写成如下形式:
m
a
x
α
∑
i
=
1
m
α
i
−
1
2
∑
i
=
1
m
∑
j
=
1
m
α
i
α
j
y
i
y
j
κ
(
x
i
,
x
j
)
条
件
{
∑
i
=
1
m
α
i
y
i
=
0
α
i
≥
0
,
i
=
1
,
2
,
…
,
m
.
(
3.1
)
max _\alpha \quad \sum_{i=1}^{m}{\alpha_i} - \frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_i\alpha_jy_iy_j\kappa (x_i,x_j)\quad\quad\quad 条件\begin{cases} \sum_{i=1}^{m}{\alpha_iy_i}=0 \\ \alpha _i \geq 0,\quad i=1,2,…,m. \end{cases} \quad\quad \quad(3.1)
maxαi=1∑mαi−21i=1∑mj=1∑mαiαjyiyjκ(xi,xj)条件{∑i=1mαiyi=0αi≥0,i=1,2,…,m.(3.1)
求解后可得到:
f
(
x
)
=
w
T
ϕ
(
x
)
+
b
=
∑
i
=
1
m
α
i
y
i
ϕ
(
x
i
)
T
ϕ
(
x
)
+
b
=
∑
i
=
1
m
α
i
y
i
κ
(
x
,
x
i
)
+
b
f(x) =w^T \phi (x)+b\\ \quad\quad\quad\quad\quad\quad\quad =\sum_{i=1}^{m}{\alpha_iy_i\phi (x_i)^T\phi (x) + b}\\ \quad\quad\quad\quad\quad =\sum_{i=1}^{m}{\alpha_iy_i\kappa (x,x_i) + b}
f(x)=wTϕ(x)+b=i=1∑mαiyiϕ(xi)Tϕ(x)+b=i=1∑mαiyiκ(x,xi)+b
那么此处的
κ
(
x
i
,
x
j
)
\kappa (x_i,x_j)
κ(xi,xj)就是核函数
3.4. 常用核函数
-
线性核函数
κ ( x i , x j ) = x i T x j \kappa (x_i,x_j)=x_i^Tx_j κ(xi,xj)=xiTxj

-
高斯核函数
κ ( x i , x j ) = e x p ( − ∣ ∣ x − y ∣ ∣ 2 2 σ 2 ) \kappa (x_i,x_j)=exp(-\frac{||x-y||^2}{2\sigma^2}) κ(xi,xj)=exp(−2σ2∣∣x−y∣∣2)

4. 软间隔与正则化
4.1. 软间隔
硬间隔要求间隔之间不存在任何错误点,要求非常严格,对于复杂的数据集(有异常点)很难有较好的分类结果,因此提出软间隔。软间隔允许部分点出现在间隔对侧,因此引入以下的松弛变量,来修改优化目标。在程序中可以使用**参数C**控制软间隔的程度。
4.2. 松弛变量
实际任务中,很多样本数据不能用一个超平面把它们完全的分开,如果数据中存在噪音点的话,就更难分开它们,也就是说在找超平面的时候会更加困难,如果考虑噪音点,会出现效果很差的超平面。如下图所示,如果考虑最上方的噪音点(圆圈),找到的超平面会很差,所以应当舍弃噪音点,绘制如下图虚线所示的超平面才是理想的结果。

因此引入松弛变量 ξ \xi ξ 来允许一些数据可以处于超平面错误的一侧,那么此时约束条件变成 y i ⋅ ( w T x i + b ) ≥ 1 − ξ i y_i\cdot(w^Tx_i+b)\geq1- \xi_i yi⋅(wTxi+b)≥1−ξi
优化目标变成:
m
i
n
w
,
b
,
ξ
1
2
∣
∣
w
∣
∣
2
+
C
∑
i
=
1
m
ξ
i
min_{w,b,\xi}\quad\frac{1}{2}||w||^{2}+C\sum_{i=1}^{m}\xi_i
minw,b,ξ21∣∣w∣∣2+Ci=1∑mξi
当C趋近于很大时:意味着分类严格遵循约束条件,不能有错误;
当C趋近于很小时:意味着可以不那么严格的遵循约束条件,有更大的错误容忍。
C是我们需要在程序中指定的一个参数。
4.3. 替代损失函数
-
hinge损失: ι h i n g e ( z ) = m a x ( 0 , 1 − z ) \iota _{hinge}(z)=max(0,1-z) ιhinge(z)=max(0,1−z)
-
指数损失: ι e x p ( z ) = e x p ( − z ) \iota _{exp}(z)=exp(-z) ιexp(z)=exp(−z)
-
对数损失: ι l o g ( z ) = l o g ( 1 + e x p ( − z ) ) \iota _{log}(z)=log(1+exp(-z)) ιlog(z)=log(1+exp(−z))
对应的图像如下图所示:

在sklearn工具包中,损失函数都有特定的包,在使用时直接导包进行对比实验,选择合适的损失函数就好,不必太过于深的了解其中的推导过程。
4.4. 修改拉格朗日乘子
L ( w , b , α , ξ , μ ) = 1 2 ∣ ∣ w ∣ ∣ 2 + C ∑ i = 1 m ξ i + ∑ i = 1 m α i ( 1 − ξ i − y i ( w T x i + b ) ) − ∑ i = 1 m μ i ξ i L(w,b,\alpha,\xi,\mu)=\frac{1}{2}||w||^{2}+C\sum_{i=1}^{m}\xi_i+\sum_{i=1}^{m}\alpha_i (1-\xi_i-y_i(w^Tx_i+b))-\sum_{i=1}^{m}\mu_i\xi_i L(w,b,α,ξ,μ)=21∣∣w∣∣2+Ci=1∑mξi+i=1∑mαi(1−ξi−yi(wTxi+b))−i=1∑mμiξi
其中 α i ≥ 0 , μ i ≥ 0 \alpha_i \geq0,\mu_i \geq 0 αi≥0,μi≥0 是拉格朗日乘子。
5. SVM具体实现
5.1. 最大边际分隔超平面
本案例绘制了二分类时追求的最大边际的分割超平面,使用的算法是线性核下的支持向量机分类。
5.1.1. 具体实现一
- 代码示例1:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm
from sklearn.datasets import make_blobs
# n_samples:待生成的样本的总数
# n_features:每个样本的特征数
# centers:表示类别数
# cluster_std:表示每个类别的方差,例如我们希望生成2类数据,
# 其中一类比另一类具有更大的方差,可以将cluster_std设置为[1.0,3.0]
# 创建40个用来分割的数据点,此处只是用来生成两个类别的数据
X, y = make_blobs(n_samples=40, centers=2, random_state=6)
# 此处如果不清楚数据集的分布,可以print一下看看
# 拟合模型,并且为了展示作用,并不进行标准化
# 使用线性核函数,也就是说对原数据集不做任何的处理
clf = svm.SVC(kernel='linear', C=1000)
clf.fit(X, y)
plt.scatter(X[:, 0], X[:, 1], c=y, s=30, cmap=plt.cm.Paired)
# 绘制decision function的结果
# 返回当前的坐标区
ax = plt.gca()
# 获取x轴的上下限
xlim = ax.get_xlim()
# 获取y轴的上下限
ylim = ax.get_ylim()
# 创造网格来评估模型
xx = np.linspace(xlim[0], xlim[1], 30)
yy = np.linspace(ylim[0], ylim[1], 30)
# 绘制棋盘
YY, XX = np.meshgrid(yy, xx)
xy = np.vstack([XX.ravel(), YY.ravel()]).T
Z = clf.decision_function(xy).reshape(XX.shape)
# 绘制决策边界和边际
ax.contour(XX, YY, Z, colors='k', levels=[-1, 0, 1], alpha=0.5,
linestyles=['--', '-', '--'])
# 绘制支持向量
ax.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], s=100,
linewidth=1, facecolors='none', edgecolors='k')
plt.show()
- 运行结果1:

5.1.2. 具体实现二
- 代码示例2:
# 1.导入基本数据处理、画图、警告处理的包
import numpy as np
import os
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
plt.rcParams['axes.labelsize']=14
plt.rcParams['xtick.labelsize']=12
plt.rcParams['ytick.labelsize']=12
import warnings
warnings.filterwarnings('ignore')
# 2.导入算法模型并进行训练
from sklearn.svm import SVC
from sklearn import datasets
iris = datasets.load_iris()
X = iris['data'][:,(2,3)]
y = iris['target']
# 先把三分类的任务改成二分类的任务
setosa_or_versicolor = (y==0)|(y==1)
X = X[setosa_or_versicolor]
y = y[setosa_or_versicolor]
svm_clf = SVC(kernel='linear',C=float('inf'))
svm_clf.fit(X,y)
# 3.画图展示
def plot_svc_decision_boundary(svm_clf,xmin,xmax,sv=False):
# 权重参数
w = svm_clf.coef_[0]
# 偏置参数,就是常数b
b = svm_clf.intercept_[0]
x0 = np.linspace(xmin,xmax,200)
decision_boundary = -w[0]/w[1] * x0 - b/w[1]
margin = 1/w[1]
gutter_up = decision_boundary + margin
gutter_down = decision_boundary - margin
if sv:
# 画出支持向量
svs = svm_clf.support_vectors_
plt.scatter(svs[:,0],svs[:,1],s=180,facecolors='r')
plt.plot(x0,decision_boundary,'k-',linewidth=2)
plt.plot(x0,gutter_up,'k--',linewidth=2)
plt.plot(x0,gutter_down,'k--',linewidth=2)
plt.figure(figsize=(6,4))
plot_svc_decision_boundary(svm_clf,0,5,True)
plt.plot(X[:,0][y==1],X[:,1][y==1],'gs')
plt.plot(X[:,0][y==0],X[:,1][y==0],'bs')
plt.axis([0,5.5,0,2])
- 运行结果2:

5.2. 非线性支持向量机
本案例使用的是带有RBF核的非线性SVC执行二分类任务,预测目标是输入的XOR数据,颜色图说明了SVC学习的决策功能。
5.2.1. 具体实现一
- 代码示例:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm
xx, yy = np.meshgrid(np.linspace(-3, 3, 500),
np.linspace(-3, 3, 500))
np.random.seed(0)
X = np.random.randn(300, 2)
Y = np.logical_xor(X[:, 0] > 0, X[:, 1] > 0)
#(译者注:可以在这里通过显示Y来查看什么是XOR数据)
# 拟合模型
clf = svm.NuSVC(gamma='auto')
clf.fit(X, Y)
# 在网格上为每个数据点绘制决策函数
Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
# 绘制热图
plt.imshow(Z, interpolation='nearest',
extent=(xx.min(), xx.max(), yy.min(), yy.max()), aspect='auto',
origin='lower', cmap=plt.cm.PuOr_r)
# 绘制数据点
contours = plt.contour(xx, yy, Z, levels=[0], linewidths=2,
linestyles='dashed')
# 绘制决策边界
plt.scatter(X[:, 0], X[:, 1], s=30, c=Y, cmap=plt.cm.Paired,
edgecolors='k')
plt.xticks(())
plt.yticks(())
plt.axis([-3, 3, -3, 3])
plt.show()
- 运行结果:

5.2.2. 具体实现二
非线性的构建方式有两种,一种是自己在数据中构建非线性,一种是使用核函数。
1. 自己构建数据集
- 简单的数据集演示
X1D = np.linspace(-4,4,9).reshape(-1,1)
# print(X1D) -> [[-4.]
# [-3.]
# [-2.]
# [-1.]
# [ 0.]
# [ 1.]
# [ 2.]
# [ 3.]
# [ 4.]]
X2D =np.c_[X1D,X1D**2]
# print(X2D)
# -> [[-4. 16.]
# [-3. 9.]
# [-2. 4.]
# [-1. 1.]
# [ 0. 0.]
# [ 1. 1.]
# [ 2. 4.]
# [ 3. 9.]
# [ 4. 16.]]
# 不同的类别
y = np.array([0,0,1,1,1,1,1,0,0])
plt.figure(figsize=(11,4))
# 画第一个子图
plt.subplot(121)
plt.grid(True,which='both')
plt.axhline(y=0,color='k')
plt.plot(X1D[:,0][y==0],np.zeros(4),'bs')
plt.plot(X1D[:,0][y==1],np.zeros(5),'g^')
plt.gca().get_yaxis().set_ticks([])
plt.xlabel(r'$x_1$',fontsize=20)
plt.axis([-4.5,4.5,-0.2,0.2])
# 画第二个子图
plt.subplot(122)
plt.grid(True,which='both')
plt.axhline(y=0,color='k')
plt.axvline(x=0,color='k')
plt.plot(X2D[:,0][y==0],X2D[:,1][y==0],'bs')
plt.plot(X2D[:,0][y==1],X2D[:,1][y==1],'g^')
plt.xlabel(r'$x_1$',fontsize=20)
plt.ylabel(r'$x_2$',fontsize=20,rotation = 0)
plt.gca().get_yaxis().set_ticks([0,4,8,12,16])
plt.plot([-4.5,4.5],[6.5,6.5],'r--',linewidth=3)
plt.axis([-4.5,4.5,-1,17])
plt.subplots_adjust(right=1)
plt.show()

左图是一维情况下的数据,右图是二维情况下的数据,红色的虚线就是决策边界,由此看出通过对数据的 变换可以达到非线性。
- 复杂的数据集演示
- 创建复杂数据集并展示
from sklearn.datasets import make_moons
X,y = make_moons(n_samples=100,noise=0.15,random_state=42)
def plot_dataset(X,y,axes):
plt.plot(X[:,0][y==0],X[:,1][y==0],'bs')
plt.plot(X[:,0][y==1],X[:,1][y==1],'g^')
plt.axis(axes)
plt.grid(True,which='both')
plt.xlabel(r'$x_1$',fontsize=20)
plt.ylabel(r'$x_2$',fontsize=20,rotation=0)
plot_dataset(X,y,[-1.5,2.5,-1,1.5])
plt.show()
-
数据集展示

-
对数据集升维并训练
from sklearn.datasets import make_moons
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
polynomial_svm_clf = Pipeline((
('poly_features',PolynomialFeatures(degree=3)),
('scaler',StandardScaler()),
('svm_clf',LinearSVC(C=10,loss='hinge'))
))
polynomial_svm_clf.fit(X,y)
- 绘制图形
def plot_predicts(clf,axes):
# 构建棋盘
x0s = np.linspace(axes[0],axes[1],100)
x1s = np.linspace(axes[2],axes[3],100)
x0,x1 = np.meshgrid(x0s,x1s)
# 把数据拉长并拼接
X = np.c_[x0.ravel(),x1.ravel()]
y_pred = clf.predict(X).reshape(x0.shape)
plt.contourf(x0,x1,y_pred,cmp=plt.cm.brg,alpha=0.2)
plot_predicts(polynomial_svm_clf,[-1.5,2.5,-1,1.5])
plot_dataset(X,y,[-1.5,2.5,-1,1.5])
- 结果展示

2. 使用核函数
- 创建复合估计器并训练
from sklearn.svm import SVC
poly_kernel_svm_clf = Pipeline([
('scaler',StandardScaler()),
# kernel = PolynomialFeatures
# coef0 :偏置项
('svm_clf',SVC(kernel='poly',degree=3,coef0=100,C=5))
])
poly_kernel_svm_clf.fit(X,y)
- 进行对比实验
poly100_kernel_svm_clf = Pipeline([
('scaler',StandardScaler()),
('svm_clf',SVC(kernel='poly',degree=10,coef0=100,C=5))
])
poly100_kernel_svm_clf.fit(X,y)
- 画图操作
plt.figure(figsize=(11,4))
plt.subplot(121)
plot_predicts(poly_kernel_svm_clf,[-1.5,2.5,-1,1.5])
plot_dataset(X,y,[-1.5,2.5,-1,1.5])
plt.title(r'$d=3,r=1,C=5$',fontsize=14)
plt.subplot(122)
plot_predicts(poly100_kernel_svm_clf,[-1.5,2.5,-1,1.5])
plot_dataset(X,y,[-1.5,2.5,-1,1.5])
plt.title(r'$d=10,r=1,C=5$',fontsize=14)
plt.show()
-
效果展示

-
结果分析
图的标题中,
d代表升的维数(只在线性核为poly的时候发挥作用),左图提升到三维,右图提升到十维;r代表偏置项;C是正则化参数,代表拟合的强度。
5.3. 软间隔
以下面两张图为例,在硬间隔的前提下,对于左图而言,无法画出决策边界,因为硬间隔要求能够完全把两类点分隔开,对于左图而言,不存在这样的线性决策边界;对于右图而言,可以画出决策边界,但是分类效果很差,出现过拟合现象,我们应该把离群的黄色点舍弃,再绘制决策边界。

可以使用超参数C控制软间隔程度:
具体步骤:
- 导入相关的包并进行模型训练
import numpy as np
from sklearn import datasets
# 带有最终估计器的转换管道
from sklearn.pipeline import Pipeline
# 标准化
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC
iris = datasets.load_iris()
# 选择其中的两个类别:petal length,prtal width
X = iris['data'][:,(2,3)]
y = (iris['target'] == 2).astype(np.float64)
print(X)
print(y)
svm_clf = Pipeline((
('std',StandardScaler()),
('linear_svc',LinearSVC(C=1))
))
svm_clf.fit(X,y)
- 对比不同C值所带来的效果差异
scaler = StandardScaler()
svm_clf1 = LinearSVC(C=1,random_state = 42)
svm_clf2 = LinearSVC(C=100,random_state = 42)
# 建立流水线
scaled_svm_clf1 = Pipeline((
('std',scaler),
('linear_svc',svm_clf1)
))
# 建立流水线
scaled_svm_clf2 = Pipeline((
('std',scaler),
('linear_svc',svm_clf2)
))
scaled_svm_clf1.fit(X,y)
scaled_svm_clf2.fit(X,y)
- 数据反变换并回传到属性
# 对数据进行反变换
b1 = svm_clf1.decision_function([-scaler.mean_ / scaler.scale_])
b2 = svm_clf2.decision_function([-scaler.mean_ / scaler.scale_])
w1 = svm_clf1.coef_[0] / scaler.scale_
w2 = svm_clf2.coef_[0] / scaler.scale_
# 按数据传回属性值里面
svm_clf1.intercept_ = np.array([b1])
svm_clf2.intercept_ = np.array([b2])
svm_clf1.coef_ = np.array([w1])
svm_clf2.coef_ = np.array([w2])
- 画图展示
plt.figure(figsize=(14,4.2))
plt.subplot(121)
plt.plot(X[:,0][y==1],X[:,1][y==1],'g^',label='Iris-Virginica')
plt.plot(X[:,0][y==0],X[:,1][y==0],'bs',label='Iris-Versicolor')
plot_svc_decision_boundary(svm_clf1,4,6,sv=False)
plt.xlabel('Petal length',fontsize=14)
plt.ylabel('Petal width',fontsize=14)
plt.legend(loc='upper left',fontsize=14)
plt.title('$C = {}$'.format(svm_clf1.C),fontsize=16)
plt.axis([4,6,0.8,2.8])
plt.subplot(122)
plt.plot(X[:,0][y==1],X[:,1][y==1],'g^')
plt.plot(X[:,0][y==0],X[:,1][y==0],'bs')
plot_svc_decision_boundary(svm_clf2,4,6,sv=False)
plt.xlabel('Petal legth',fontsize=14)
plt.title('$C = {}$'.format(svm_clf2.C),fontsize=16)
plt.axis([4,6,0.8,2.8])
-
结果展示

-
结果分析
在右图,使用较高的C值,分类器会减少误分类,但最终会有较小的间隔;在左图,使用较低的C值,间隔要大得多,但是很多实例最终会出现在间隔之内。 软间隔SVM允许部分点分布在间隔内部,此时可以解决硬间隔SVM的问题(只需将异常点放到间隔内部即可),因为间隔内部的点对于SVM的思想来说是一种错误,所以我们希望位于间隔内部的点尽可能少,其实是一种折中,即在错误较少的情况下获得不错的划分超平面。
6. 高斯核函数
6.1. 特征变换
- 利用相似度来变换特征
- 选择一份一维数据集,并在 x 1 x_1 x1=-2 和 x 1 x_1 x1=1 处为其添加两个高斯函数
- 接下来,让我们将相似度函数定义为
γ
\gamma
γ=0.3的径向基函数(
RBF)
ϕ γ ( x , ι ) = e x p ( − γ ∣ ∣ x − ι ∣ ∣ 2 ) \phi \gamma(x,\iota)=exp(-\gamma||x-\iota||^2) ϕγ(x,ι)=exp(−γ∣∣x−ι∣∣2)
例如: x 1 x_1 x1=-1:它位于距第一个地标距离为1的地方,距第二个地标距离为2.因此,其新特征是 x 2 = e x p ( − 0.3 × 1 2 ) ≈ 0.74 x_2 = exp(-0.3\times1^2)≈0.74 x2=exp(−0.3×12)≈0.74 并且 x 3 = e x p ( − 0.3 × 2 2 ) ≈ 0.30 x_3=exp(-0.3\times2^2)≈0.30 x3=exp(−0.3×22)≈0.30

6.2. 算法模拟
高斯核函数的模拟:
# 定义高斯核函数
def gaussian_rbf(x,landmark,gamma):
return np.exp(-gamma * np.linalg.norm(x - landmark,axis=1)**2)
# 定义gamma值
gamma = 0.3
# 生成200个数据点
x1s = np.linspace(-4.5,4.5,200).reshape(-1,1)
# 选择两个地标
x2s = gaussian_rbf(x1s,-2,gamma)
x3s = gaussian_rbf(x1s,1,gamma)
XK = np.c_[gaussian_rbf(X1D,-2,gamma),gaussian_rbf(X1D,1,gamma)]
yk = np.array([0,0,1,1,1,1,1,0,0])
plt.figure(figsize=(11,4))
plt.subplot(121)
plt.grid(True,which='both')
plt.axhline(y=0,color='k')
plt.scatter(x=[-2,1],y=[0,0],alpha=0.5,c='red')
plt.plot(X1D[:,0][yk==0],np.zeros(4),'bs')
plt.plot(X1D[:,0][yk==1],np.zeros(5),'g^')
plt.plot(x1s,x2s,'g--')
plt.plot(x1s,x3s,'b:')
plt.xlabel(r'$x_1$',fontsize=20)
plt.ylabel(r'$Similarrity$',fontsize=14)
plt.annotate(
r'$\mathbf{x}$',
xy=(X1D[3,0],0),
xytext=(-0.5,0.20),
ha='center',
arrowprops=dict(facecolor='black',shrink=0.1),
fontsize=18
)
plt.text(-2,0.9,'$x_2$',ha='center',fontsize = 20)
plt.text(1,0.9,'$x_3$',ha='center',fontsize = 20)
plt.axis([-4.5,4.5,-0.1,1.1])
plt.subplot(122)
plt.grid(True,which='both')
plt.axhline(y=0,color='k')
plt.axvline(x=0,color='k')
plt.plot(XK[:,0][yk==0],XK[:,1][yk==0],'bs')
plt.plot(XK[:,0][yk==1],XK[:,1][yk==1],'g^')
plt.xlabel(r'$x_2$',fontsize=20)
plt.ylabel(r'$x_3$',fontsize=20,rotation=0)
plt.annotate(
r'$\phi \left (\mathbf{x} \right)$',
xy=(XK[3,0],XK[3,1]),
xytext=(0.65,0.50),
ha='center',
arrowprops=dict(facecolor='black',shrink=0.1),
fontsize=18
)
plt.plot([-0.1,1.1],[0.57,-0.1],'r--',linewidth=3)
plt.axis([-0.1,1.1,-0.1,1.1])
plt.subplots_adjust(right=1)
plt.show()
效果展示:
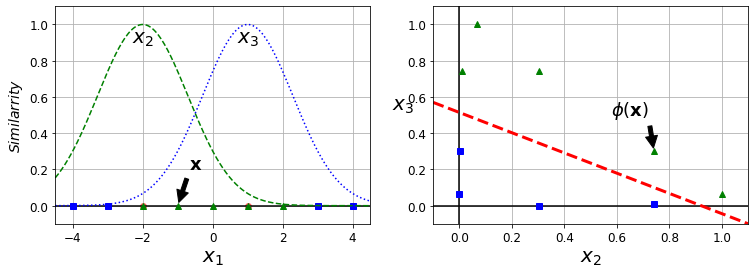
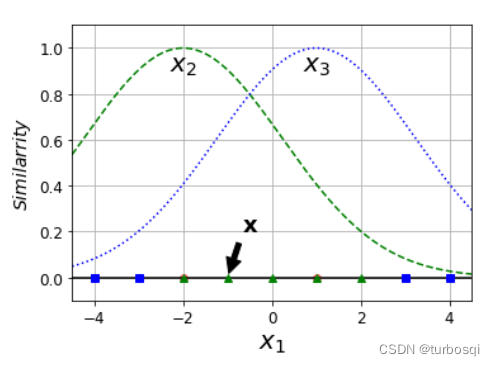
结果分析:
上图中,左上是gamma=0.3时候的函数涵盖范围,左下是gamma=0.1时候的函数涵盖范围。可以看出当gamma变小的时候,函数涵盖的数据会变广,过拟合的风险会变得越来越小;当gamma变大的时候,过拟合的风险会变得越来越大。总之,增加gamma,y使高斯曲线变窄,因此每个实例的影响范围都较小,决策边界最终变得更不规则,在个别实例周围摆动。减少gamma,y使高斯曲线变宽,因此实例具有更大的影响范围,并且决策边界更加平滑。
6.3. 对比分析
以下进行对比实验:
from sklearn.svm import SVC
gamma1,gamma2 = 0.1,5
C1,C2 = 0.001,1000
hyperparams = (gamma1,C1),(gamma2,C1),(gamma1,C2),(gamma2,C2)
svm_clfs = []
for gamma,C in hyperparams:
rbf_kernel_svm_clf = Pipeline([
('scaler',StandardScaler()),
('svm_clf',SVC(kernel='rbf',gamma=gamma,C=C))
])
rbf_kernel_svm_clf.fit(X,y)
svm_clfs.append(rbf_kernel_svm_clf)
plt.figure(figsize=(15,12))
for i,svm_clf in enumerate(svm_clfs):
plt.subplot(221 + i)
plot_predicts(svm_clf,[-1.5,2.5,-1,1.5])
plot_dataset(X,y,[-1.5,2.5,-1,1.5])
gamma,C = hyperparams[i]
plt.title(r'$\gamma = {}, C = {}$'.format(gamma,C),fontsize=16)
plt.show()
效果展示:

结果分析:
由左上和右上(或左下和右下)的图对比中,在正则化参数相同的条件下,增大gamma值,决策边界变得不规则,在个别实例周围摆动,过拟合的风险就会变大。




![引用参考文献[1,2]或者[1-3]](https://img-blog.csdnimg.cn/3e295979efde43d9be2bb32548223f52.png)