目录

一、介绍

二、解题思路

                介绍动态规划法

三、代码实现

---

一、介绍

所谓的青蛙跳台阶问题，就是指一只青蛙一次可以跳上1级台阶，也可以跳上2级（最多只能跳2级）。求该青蛙跳上一个n级的台阶总共有多少种跳法。

二、解题思路

首先得找其规律，这里我用图来帮助大家理解。

①若n = 1，只有一级台阶，很显然就只有一种跳法

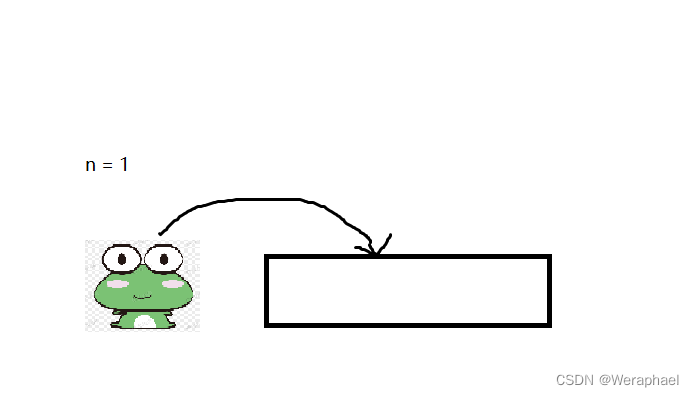
②若 n = 2，一共有两级台阶，共有两种跳法

第一种：一级一级跳（黑线）

第二种：一口气跳2级（红线）

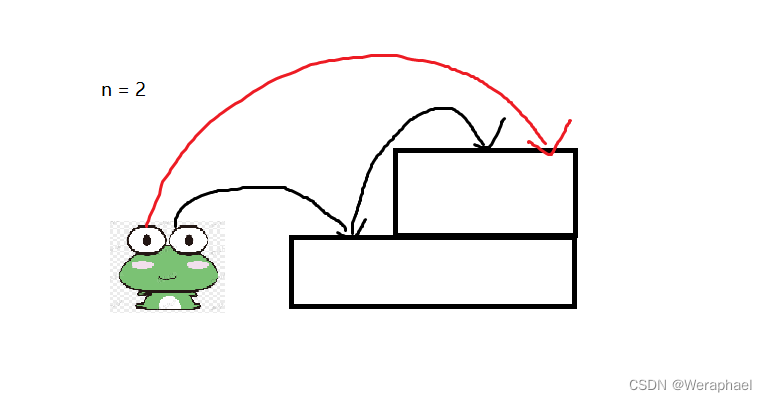
③若n = 3，一共有三级台阶，共有三种跳法

第一种：一级一级跳（黑线）

第二种：先跳两级，再跳一级（红线）

第三种：先跳一级，再跳两级（黄线）

 

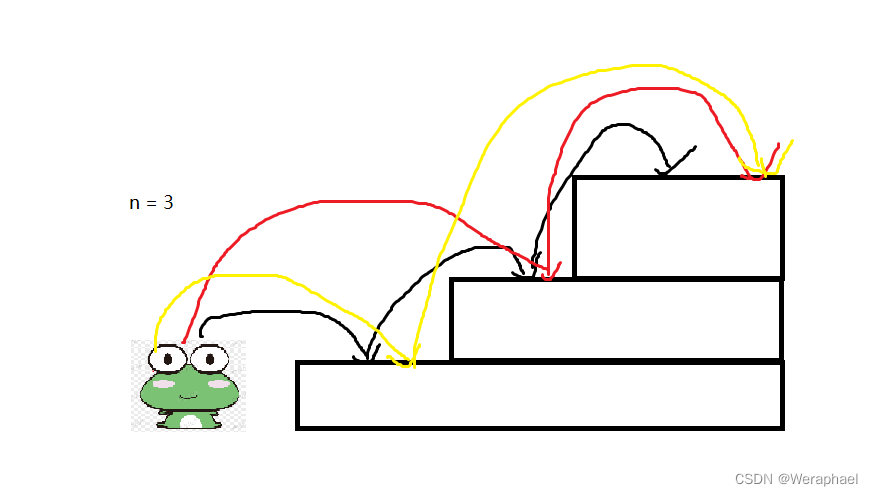
 大家看到这里，心里想是不是有n个台阶，就对应有n种跳法。让我们接着往下看

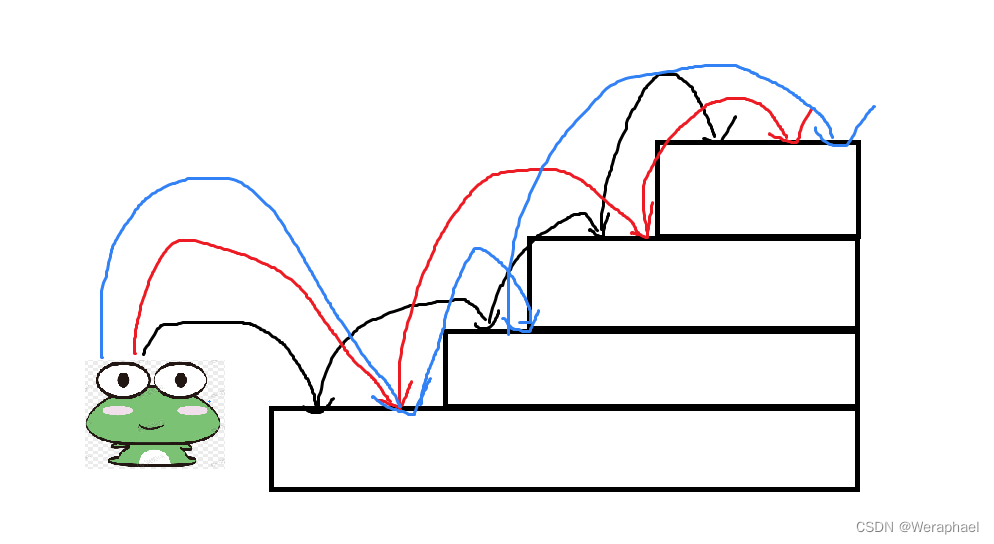
④若n = 4，一共有四级台阶，共有5种跳法

第一种：一级一级跳（黑线）

第二种：先跳一级，再跳两级，最后再跳一级（红线）

第三种：先跳一级，再跳一级，最后再跳两级（蓝线）

第四种：先跳两级，再跳一级，最后再跳一级

第五种：先跳两级，再跳两级

（太乱了未画完，大家明白就好）

介绍动态规划法：

大家数着数着有没有发现，是不是快要把自己给数懵了，那有没有什么好的方法呢？这里我就要给大家介绍动态规划法：用上一步的结果，来快速计算得到下一步的结果。

举个例子

看下图，若台阶数n = 4，假设小青蛙先跳一级台阶，接下来它是不是还有三级台阶要跳，而三级台阶跳法个数刚刚我们算过了，一共有3种跳法，或者小青蛙也可以先跳二级台阶，那么接下来它面对的台阶数为二，而二级台阶数的跳法就有2种。所以对于四级台阶数，小青蛙的跳法一共是3+2=5种跳法。

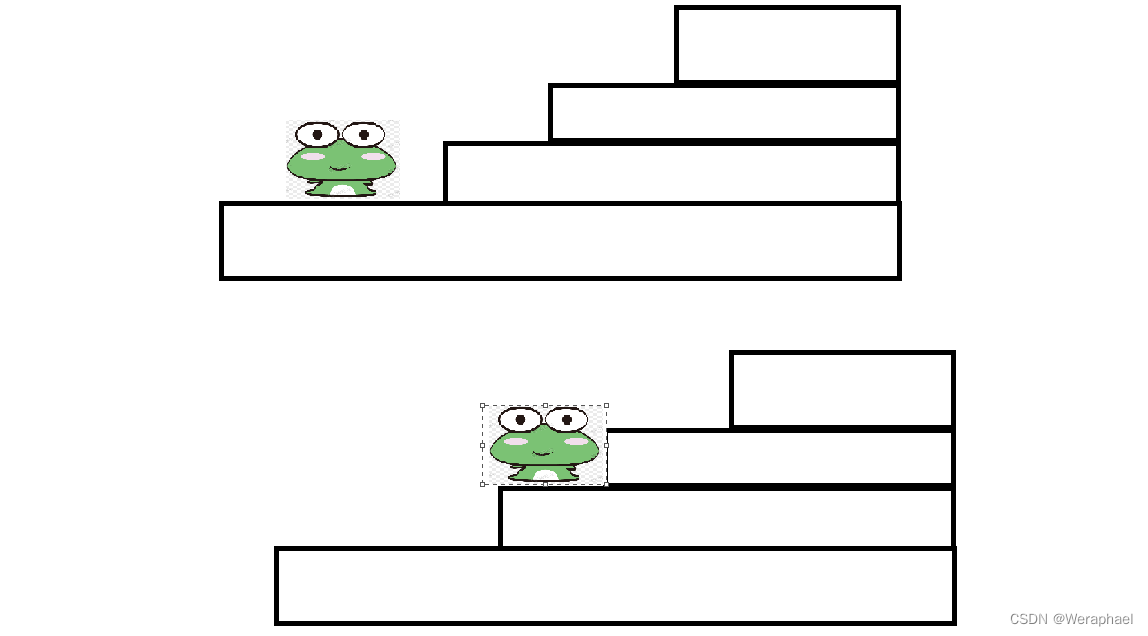
 接下来回到解题思路上来

⑤ 若n = 5，一共有五级台阶，共有8种跳法

（这里分析就省略了，大家还可以用动态规划法来分析）

看到这里大家是不是发现规律了

n<=3时，就对应其台阶数

n>3时，不就是前一个数的跳法加上后一个数的跳法，不就是斐波那契数

（*深入学习函数（3）-- 递归篇（图文详解）_Weraphael的博客-CSDN博客）

既然知道了规律，就赶紧敲代码来验证吧！

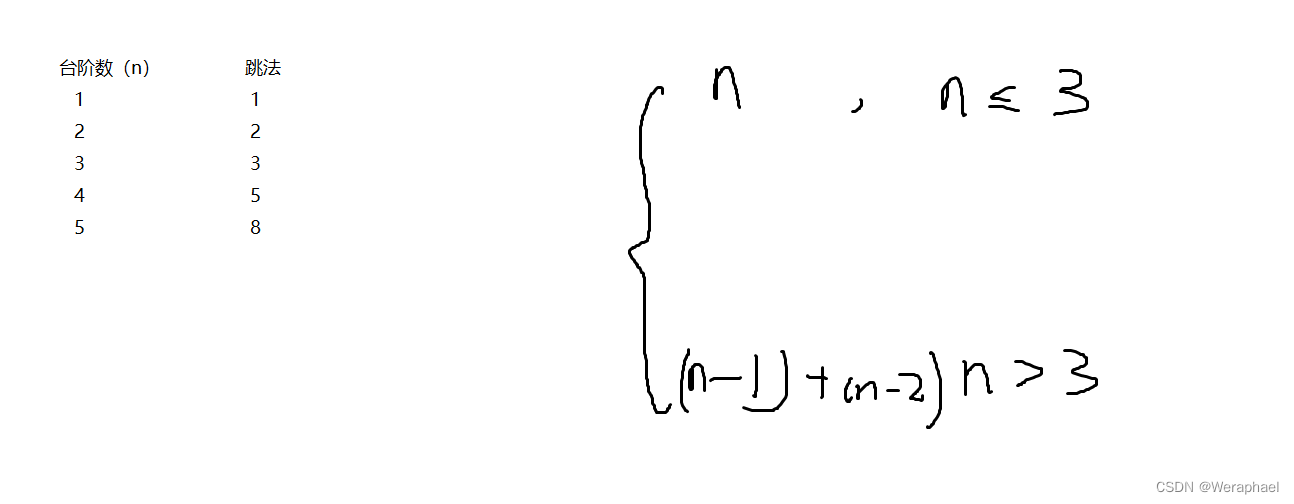
三、代码实现：

#include <stdio.h>
int Jump(int n)
{
	if (n <= 3)
	{
		return n;  //返回对应的台阶数
	}
	else
		return Jump(n - 1) + Jump(n - 2);//斐波那契问题
}
int main()
{
	int n = 0;//台阶数
	//输入台阶数
	scanf("%d", &n);
	int ret = Jump(n);
	printf("一共有%d种跳法。\n", ret);
	return 0;
}

接下来看看代码效果（部分）：

 显然符合预期！

看到这里，你是否真的学会了小青蛙跳台阶问题呢？