很多人都对递归有了解,但是为尾递归很少,所以这次来专门讲一讲关于尾递归的一些问题。
什么是尾递归
如果一个函数中所有递归形式的调用都出现在函数的末尾,我们称这个递归函数是尾递归的。因为在一些题目的做法中,我们可以发现递归的使用有局限性,有时候会占用相当大的空间。比如斐波那契问题,代码很容易用递归去写,但是浪费了大量的内存,一个数会重复计算多次,所以我们来使用尾递归。这里引用一个我看别人说的一句话,我认为非常对普通递归的结果是返回值,尾递归的结果是参数。完全可以这样理解。
尾递归的优化原理
尾递归优化的概念 尾递归是指递归调用出现在函数体的最后,并且是返回值的一部分。 它是一种特殊的递归形式,不会在回归过程中做其他操作或表达式的计算。尾调用优化 尾调用是尾递归优化的基础。 尾调用是指函数调用出现在调用者函数的最后,并且该调用的返回值直接被当前函数返回。 尾调用优化的目的是将递归调用转化为尾调用,从而减少函数调用栈的使用。 通过尾调用优化,实现函数的尾递归优化,可以避免递归调用带来的栈溢出问题。
举例子来说明一下:
阶乘问题(源码一律放后面)
求一个数的阶乘,普通求法非常简单不讲。
首先设置一个函数,你用函数传参的性质,建立出这个阶乘的函数模型,当X等于零的时候那么就直接返回一,也就是结束标志,若X没有为零的时候就进行递归操作
那么尾递归是怎么实现的呢?
注意之前说的一句话,普通递归的结果是返回值,尾递归的结果是参数,所以为递归和尾递归的一个区别是为地规会多一个参数,将这个函数不变,但是多传一个变量,那么我们就想办法让最后的机会用这个变量表示出来,所以说当n等于1的时候我们直接返回那个变量,否则就继续往下传参,我们将参数一一对应,这里面用逗号表达式的知识,这个变量随着n减减下来最后会等于1也就是说,这个函数的结果就是最后ret的那个值,就是阶乘。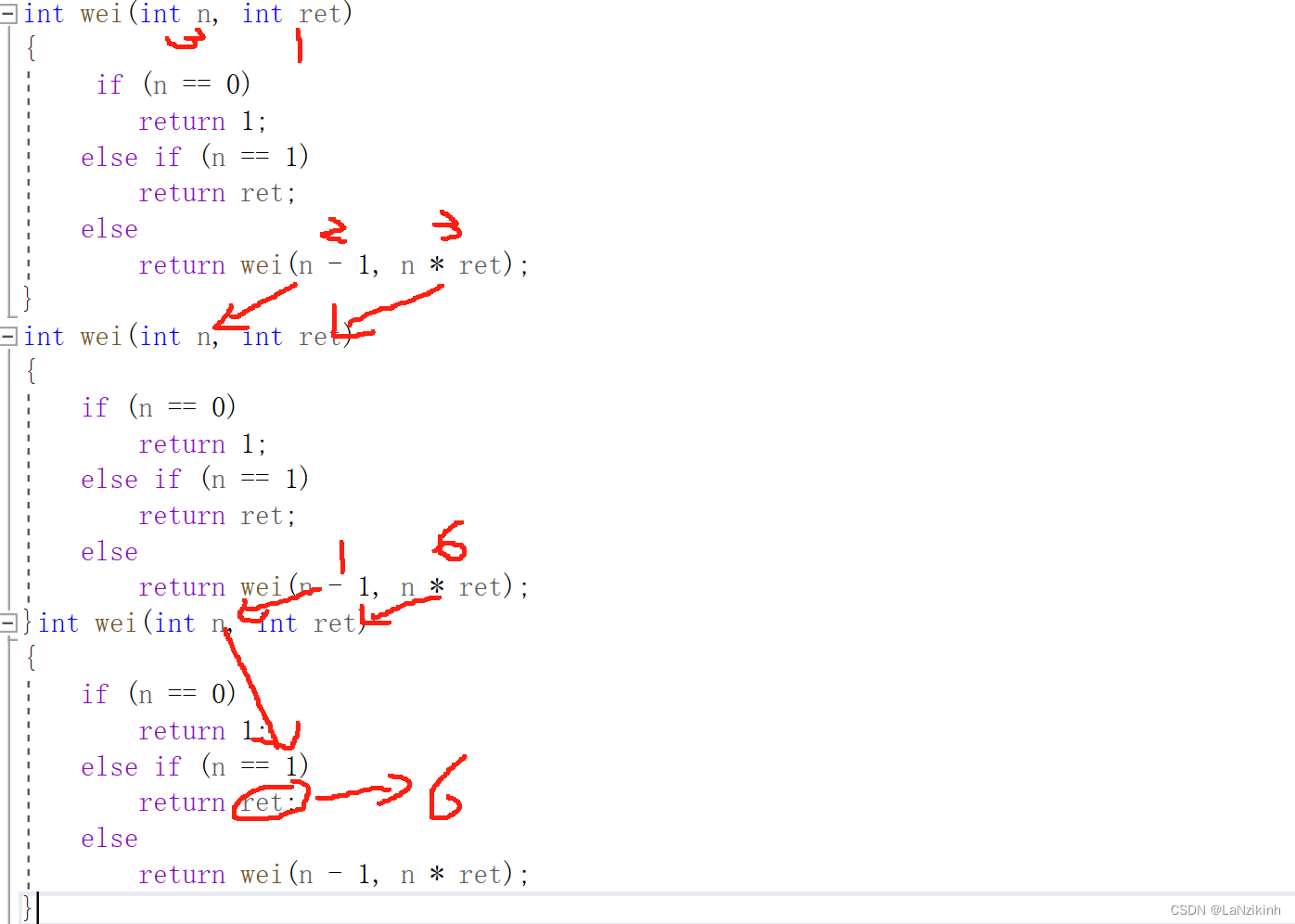
斐波那契问题(源码一律放后面)
什么是斐波那契数?
指的是这样的一个数列:1、1、2、3、5、8、13、21、34、……,这个数列从第 3 项开始,每一项都等于前面两项之和。
做法
递归太简单直接摆
普通做法
利用一个前面加后面一直往后推的一个思想,把加的值,慢慢传递,最开始都是从一n大于二的时候意思就是说从第三个数开始,把第三个数等于前两个数相加,第二个数传给第一个数第三个数再传给第二个数以此类推,最后再返回第三个数就可以了。
尾递归
这里跟普通的相比也是多传两个参数,因为最开始的两个数都是一,我们必须提前知道,其实做法和普通方法的思维是一致的也是相加,但是最后需要用这个b来表示出来,用逗号表达式的这个知识和函数传参
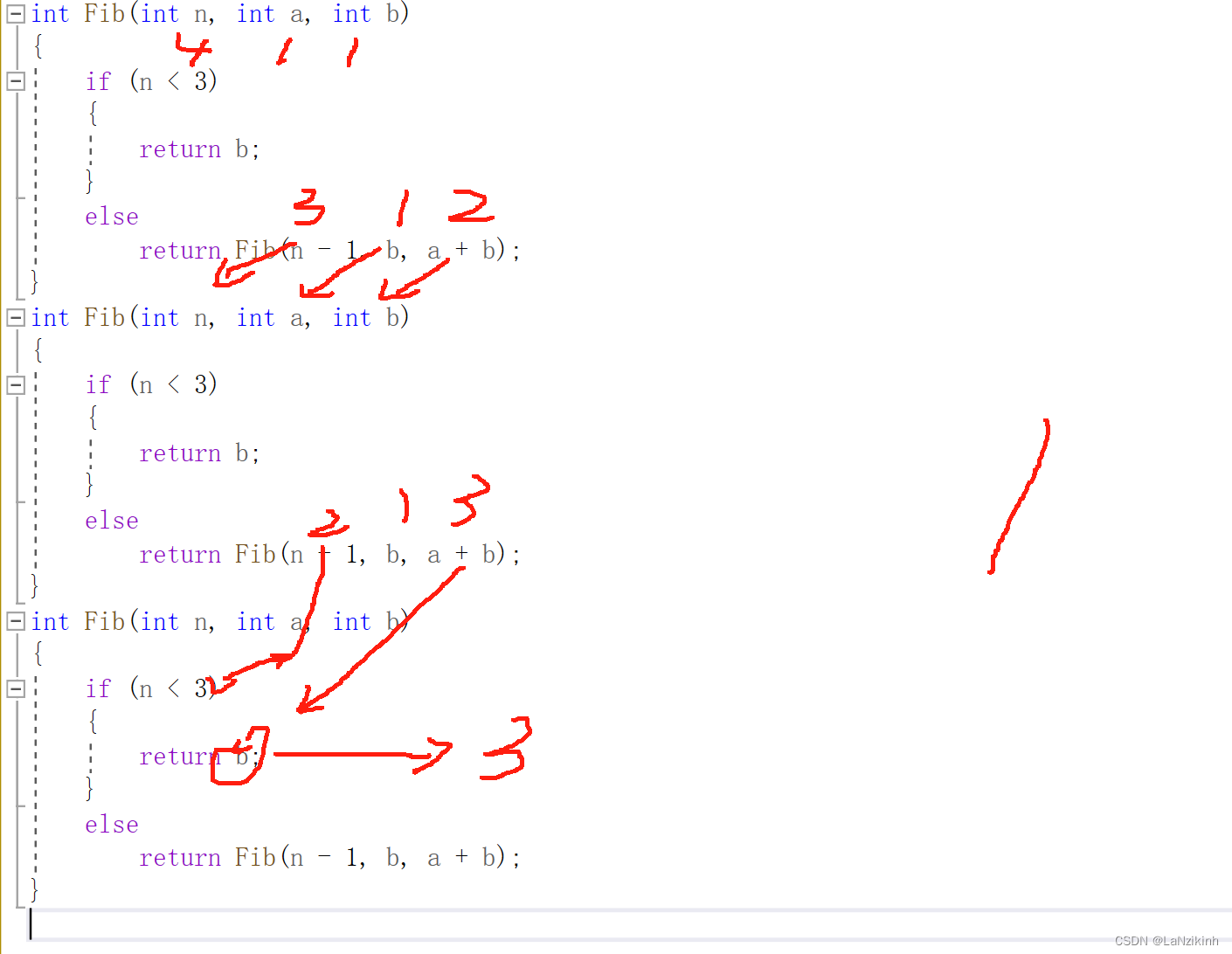
源码
阶乘:
//int test(int x)
//{
// if (x == 0)
// {
// return 1;
// }
// return x * test(x - 1);
//
//}
//int main()
//{
// int n = 0;
// scanf_s("%d", &n);
// int a = test(n);
// printf("%d", a);
//
// return 0;
//}
//int main()
//{
// int n = 0;
// scanf_s("%d", &n);//n=4
// int sum = 1;
// for (int i = 1; i<=n; i++)
// {
// sum = sum * i;
// }
//
// printf("%d", sum);
//
// return 0;
//}
//int wei(int n, int ret)
//{
// if (n == 0)
// return 1;
// else if (n == 1)
// return ret;
// else
// return wei(n - 1, n * ret);
//}
斐波那契:
int Fib(int n, int a, int b)
{
if (n < 3)
{
return b;
}
else
return Fib(n - 1, b, a + b);
}
int main()
{
int n = 0;
int ret = 0;
scanf_s("%d", &n);
ret = Fid(n,1,1);
printf("%d\n", ret);
return 0;
return 0;
}
//int Fid(int n)
//{
// if (n <= 2)
// return 1;
// else
// return Fid(n - 1) + Fid(n - 2);
//}
//int Fid(int n)
//{
// int a, b, c = 1;
// while (n > 2)
// {
// c = a + b;
// a = b;
// b = c;
// n--;
// }
// return c;
//}