代码随想录算法训练营第十四天|二叉树基础-二叉树迭代-二叉树

news2024/11/16 5:36:51

文章目录

  • 二叉树基础
    • 二叉树种类
      • 满二叉树
      • 完全二叉树
      • 二叉搜索树
      • 平衡二叉搜索树
    • 二叉树的存储方式
      • 链式存储
      • 顺序存储
    • 二叉树的遍历方式
    • 二叉树的定义
  • 二叉树的递归遍历
    • 144.二叉树的前序遍历
      • 代码：
    • 145.二叉树的后序遍历
      • 代码：
    • 94. 二叉树的中序遍历
      • 代码
  • 二叉树的迭代遍历
    • 前序遍历（迭代法）-中左右->中右左（模拟出入栈）
      • 代码
    • 后序遍历（迭代法）
      • 思路：
      • 代码：
    • 中序遍历（迭代法）
      • 代码：
  • 二叉树的统一迭代法-画图理解增加熟练
      • 前序遍历写法-右左中（反过来）
      • 中序遍历写法-右中左
    • 后序遍历-中右左

二叉树基础

二叉树种类

满二叉树

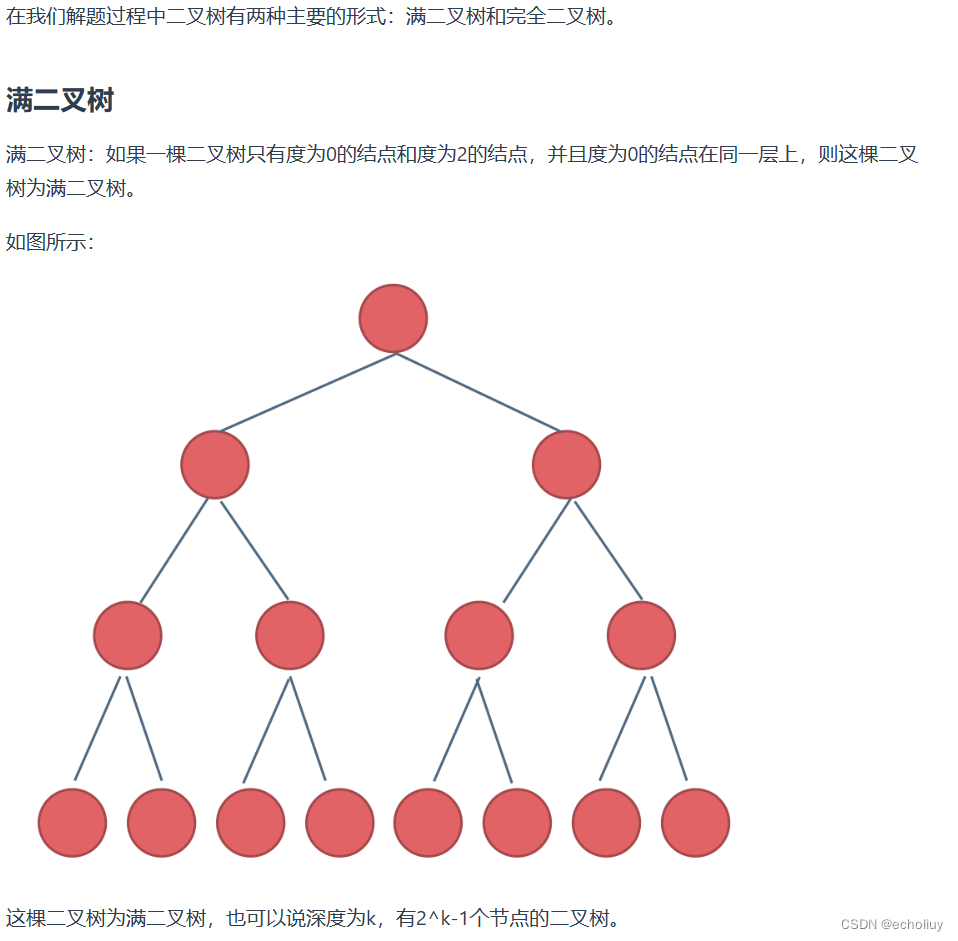
在这里插入图片描述

完全二叉树

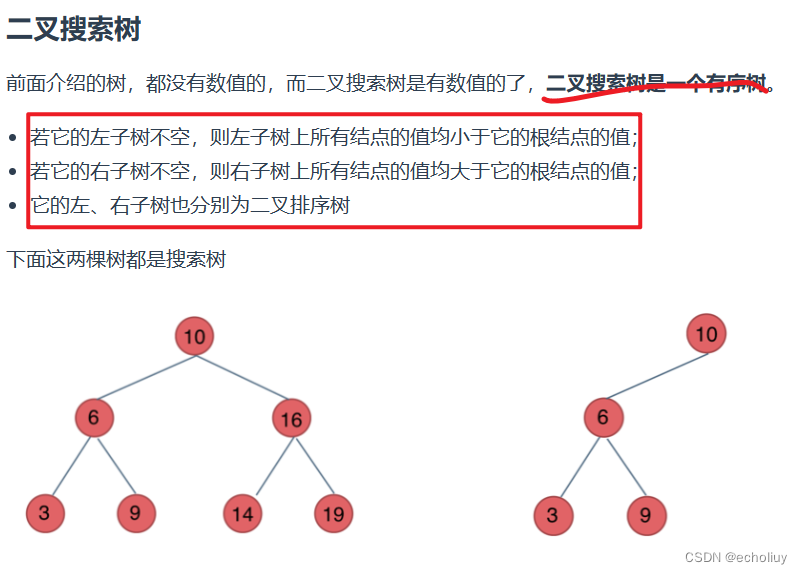
在这里插入图片描述

二叉搜索树

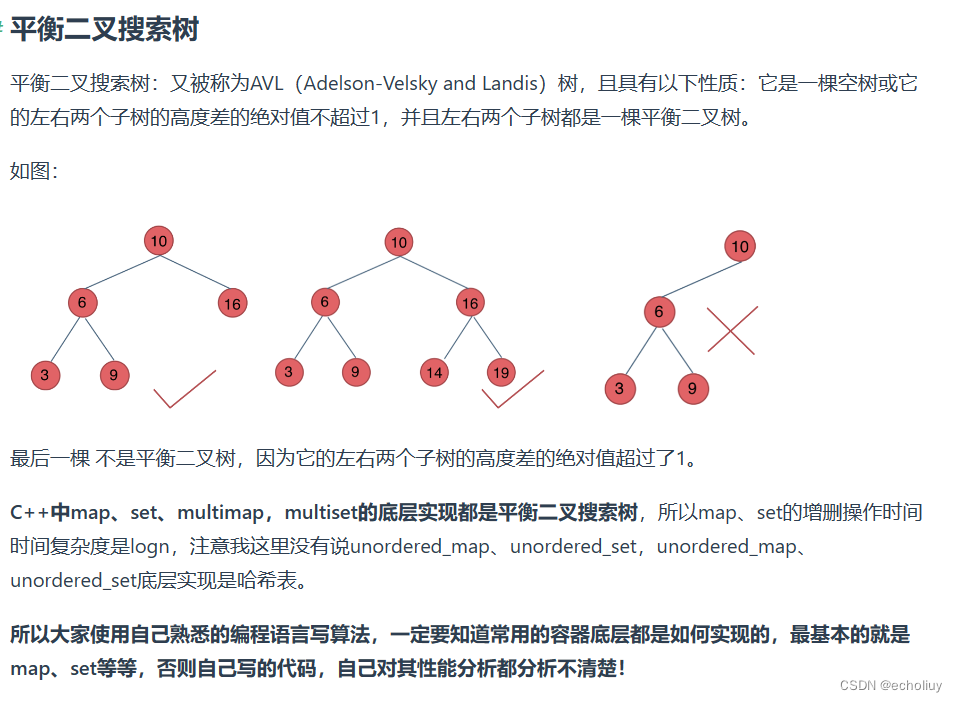
在这里插入图片描述

平衡二叉搜索树

在这里插入图片描述

二叉树的存储方式

链式存储

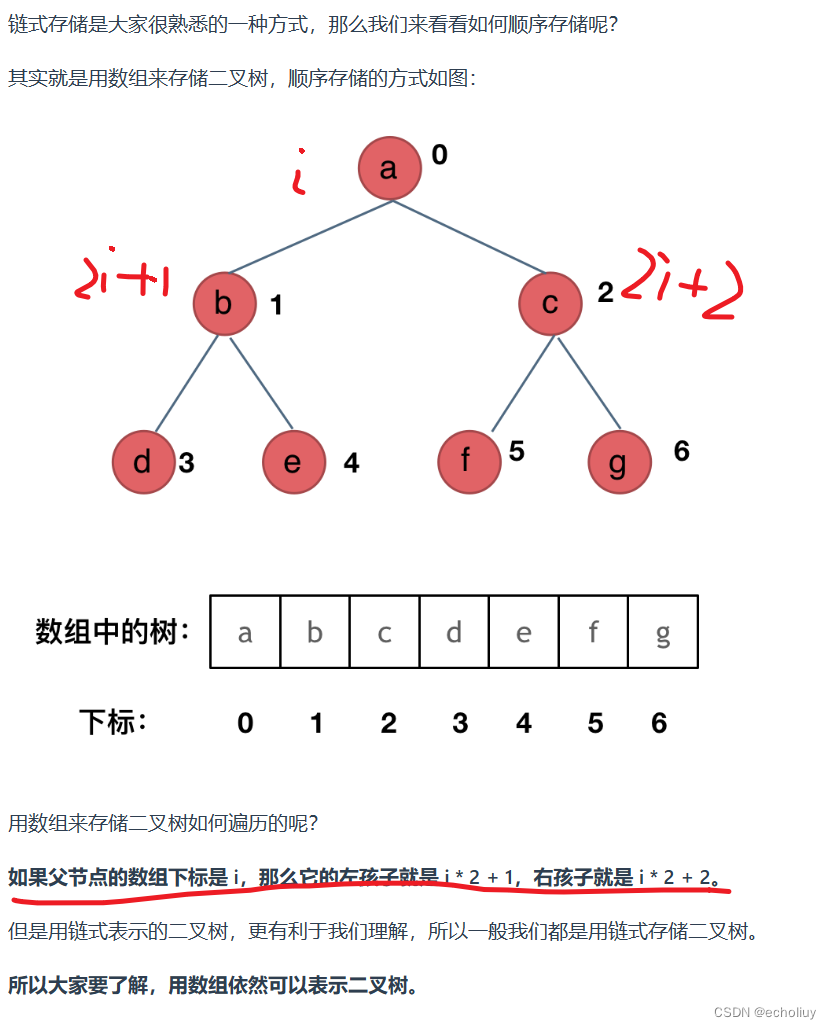
在这里插入图片描述

顺序存储

在这里插入图片描述

二叉树的遍历方式

二叉树主要有两种遍历方式：

  1. 深度优先遍历：先往深走，遇到叶子节点再往回走。
  2. 广度优先遍历：一层一层的去遍历。

这两种遍历是图论中最基本的两种遍历方式，后面在介绍图论的时候 还会介绍到。

那么从深度优先遍历和广度优先遍历进一步拓展，才有如下遍历方式：

  1. 深度优先遍历
    • 前序遍历（递归法，迭代法）
    • 中序遍历（递归法，迭代法）
    • 后序遍历（递归法，迭代法）
  2. 广度优先遍历
    • 层次遍历（迭代法）
      在深度优先遍历中：有三个顺序，前中后序遍历， 有同学总分不清这三个顺序，经常搞混，我这里教大家一个技巧。

这里前中后，其实指的就是中间节点的遍历顺序，只要大家记住 前中后序指的就是中间节点的位置就可以了。

看如下中间节点的顺序，就可以发现，中间节点的顺序就是所谓的遍历方式

  • 前序遍历：中左右
  • 中序遍历：左中右
  • 后序遍历：左右中
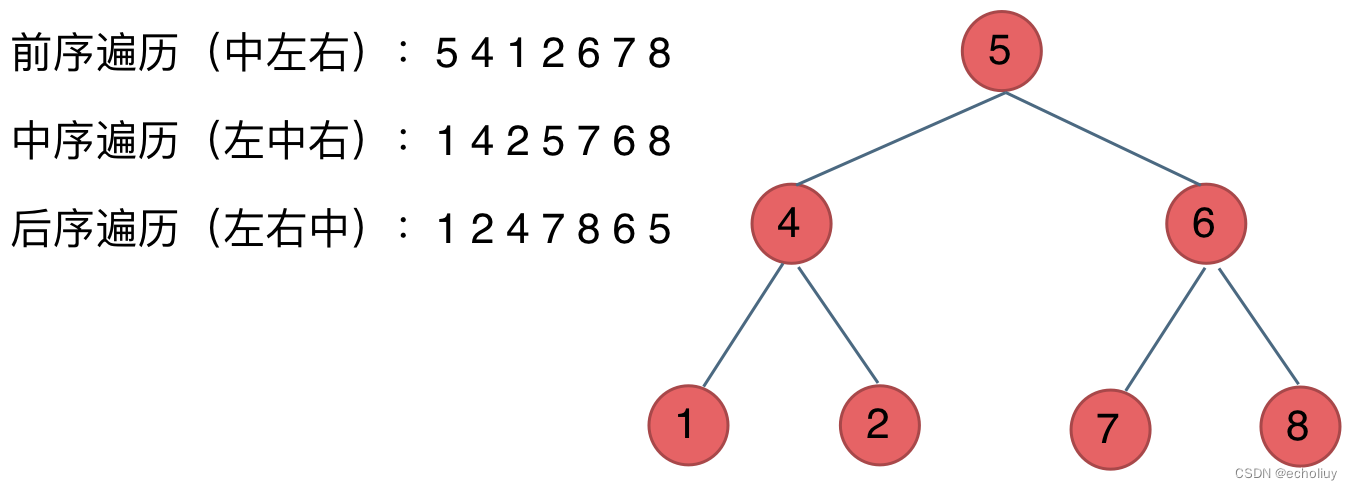
    在这里插入图片描述

二叉树的定义

public class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    TreeNode() {}
    TreeNode(int val) { this.val = val; }
    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

二叉树的递归遍历

在这里插入图片描述

144.二叉树的前序遍历

前序遍历，中左右

代码：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();//结果数组
        preorder(root,result);//开始从根节点遍历
        return result;
    }
    public void preorder(TreeNode root,List<Integer> res){
        if(root==null){
            return; //直接返回
        }
        res.add(root.val);//添加根节点
        preorder(root.left,res);
        preorder(root.right,res);
    }
}

145.二叉树的后序遍历

左右中

代码：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        postOrder(root,res);
        return res;
    }
    public void postOrder(TreeNode root,List<Integer> res){
        if(root==null){
            return;
        }
        postOrder(root.left,res);
        postOrder(root.right,res);
        res.add(root.val);
    }
}

94. 二叉树的中序遍历

左中右

代码

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        inOrder(root,res);
        return res;
    }
    public void inOrder(TreeNode root,List<Integer> res){
        if(root==null){
            return;
        }
        inOrder(root.left,res);
        res.add(root.val);
        inOrder(root.right,res);
    }
}

二叉树的迭代遍历

前序遍历（迭代法）-中左右->中右左（模拟出入栈）

我们先看一下前序遍历。

前序遍历是中左右，每次先处理的是中间节点，
那么先将根节点放入栈中，
然后先将右孩子加入栈，再加入左孩子。

为什么要先加入 右孩子，再加入左孩子呢？ 因为这样出栈的时候才是中左右的顺序。

动画如下：
在这里插入图片描述

代码

// 前序遍历顺序：中-左-右，入栈顺序：中-右-左
class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> res=new ArrayList<>();
        if(root==null){
            return res;
        }
        Stack<TreeNode> stack=new Stack<>();
        stack.push(root);//加入根节点
        while(!stack.isEmpty()){
            //中
            TreeNode node=stack.pop();//弹出根节点
            res.add(node.val);//储存根节点的数值
            //右
            if(node.right!=null){
                stack.push(node.right);
            }
            //左
            if(node.left!=null){
                stack.push(node.left);
            }
        }
        return res;
    }
}

后序遍历（迭代法）

思路：

前序遍历的数组储存是中左右，那么把函数翻转，则变成数组储存是中右左，再将数组进行翻转，则变成左右中。
在这里插入图片描述

代码：

// 后序遍历顺序 左-右-中 入栈顺序：中-左-右 出栈顺序：中-右-左， 最后翻转结果
class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        Stack<TreeNode> stack=new Stack<>();
        if(root==null){
            return res;
        }
        stack.push(root);
        while(!stack.isEmpty()){
            TreeNode node = stack.pop();
            res.add(node.val);
            if(node.left!=null){
                stack.push(node.left);
            }
            if(node.right!=null){
                stack.push(node.right);
            }
        }
        Collections.reverse(res);//反转数组
        return res;
    }
}

中序遍历（迭代法）

为了解释清楚，我说明一下 刚刚在迭代的过程中，其实我们有两个操作：

  1. 处理：将元素放进result数组中
  2. 访问：遍历节点
    分析一下为什么刚刚写的前序遍历的代码，不能和中序遍历通用呢，因为前序遍历的顺序是中左右，先访问的元素是中间节点，要处理的元素也是中间节点，所以刚刚才能写出相对简洁的代码，因为要访问的元素和要处理的元素顺序是一致的，都是中间节点。

那么再看看中序遍历，中序遍历是左中右，先访问的是二叉树顶部的节点，然后一层一层向下访问，直到到达树左面的最底部，再开始处理节点（也就是在把节点的数值放进result数组中），这就造成了处理顺序和访问顺序是不一致的。

那么在使用迭代法写中序遍历，就需要借用指针的遍历来帮助访问节点，栈则用来处理节点上的元素。

动画如下：
在这里插入图片描述

代码：

// 中序遍历顺序: 左-中-右 入栈顺序： 左-右
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        if (root == null){
            return result;
        }
        Stack<TreeNode> stack = new Stack<>();
        TreeNode cur = root;
        while (cur != null || !stack.isEmpty()){
           if (cur != null){
               stack.push(cur);
               cur = cur.left;
           }else{
               cur = stack.pop();
               result.add(cur.val);
               cur = cur.right;
           }
        }
        return result;
    }
}

二叉树的统一迭代法-画图理解增加熟练

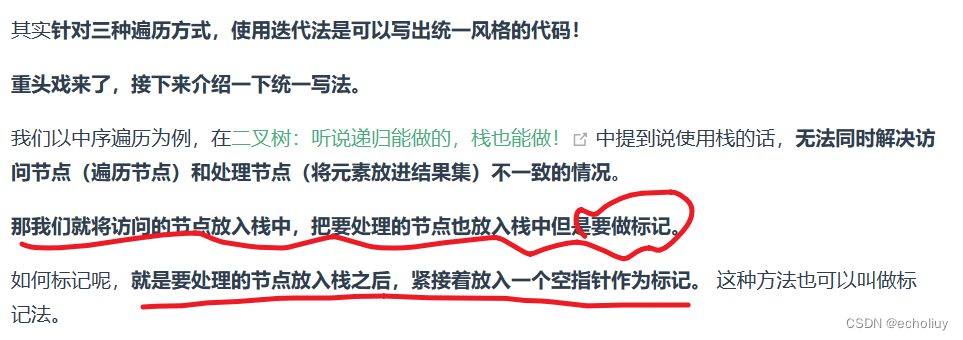
在这里插入图片描述

前序遍历写法-右左中（反过来）

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> res = new LinkedList<>();
        Stack<TreeNode> stack = new Stack<>();
        if(root!=null){
            stack.push(root);
        }
        while(!stack.isEmpty()){
            TreeNode node=stack.peek();//栈中的第一个节点
            if(node!=null){
                stack.pop();//弹出避免重复，下面再将右左中节点添加到栈中
                if(node.right!=null){//添加右节点，空节点不入栈
                    stack.push(node.right); 
                }
                if(node.left!=null){//添加左节点，空节点不入栈
                    stack.push(node.left);
                }
                stack.push(node);//添加中节点
                stack.push(null);//中节点还没有处理，添加空节点null做标记
            }else{
                stack.pop();//弹出null
                node=stack.peek();//重新取出栈中元素
                stack.pop();//取出后再弹出
                res.add(node.val);
            }
        }
        return res;
    }
}

中序遍历写法-右中左

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        Stack<TreeNode> stack = new Stack<>();
        if(root!=null){//先放入根节点
            stack.push(root);
        }
        while(!stack.isEmpty()){
            TreeNode node = stack.peek();//查找第一个结点
            if(node!=null){
                stack.pop();//弹出重复节点，按顺序放入右中左
                if(node.right!=null){
                    stack.push(node.right);
                }
                stack.push(node);
                stack.push(null);
                if(node.left!=null){
                    stack.push(node.left);
                }
            }else{
                stack.pop();
                node = stack.peek();
                stack.pop();
                res.add(node.val);
            }
        }
        return res;
    }
}

后序遍历-中右左

class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        Stack<TreeNode> stack = new Stack<>();
        if(root!=null){//先放入根节点
            stack.push(root);
        }
        while(!stack.isEmpty()){
            TreeNode node = stack.peek();//查找第一个结点
            if(node!=null){
                stack.pop();//弹出重复节点，按顺序放入中右左
                stack.push(node);
                stack.push(null);
                if(node.right!=null){
                    stack.push(node.right);
                }
                if(node.left!=null){
                    stack.push(node.left);
                }
            }else{
                stack.pop();
                node = stack.peek();
                stack.pop();
                res.add(node.val);
            }
        }
        return res;
    }
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1408487.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Linux中并发程序设计

Linux中并发程序设计

进程的创建和回收 进程概念 概念 程序 存放在磁盘上的指令和数据的有序集合&#xff08;文件&#xff09; 静态的 进程 执行一个程序所分配的资源的总称 动态的进程和程序比较 注&#xff1a;进程是存在RAM中&#xff0c;程序是存放在ROM(flash)中的进程内容 BSS段&#xff…
阅读更多...
Unity通用渲染管线升级URP、HDRP

Unity通用渲染管线升级URP、HDRP

Unity通用渲染管线升级URP、HDRP 一、Build-in Pipline升级到 URP 一、Build-in Pipline升级到 URP 安装URP包 升级所有材质&#xff08;升级完成后材质会变成紫红色&#xff0c;Shader丢失&#xff0c;此为正常现象&#xff09; 创建 UniversalRenderPipelineAsset 配置文…
阅读更多...
Origin:调整颜色刻度线间距和小数点

Origin:调整颜色刻度线间距和小数点

如何设置或修改Color Scale 的间距和小数位&#xff1f; 答&#xff1a;&#xff08;1&#xff09;更改间距&#xff1a;左键双击刻度标线——级别——“显示主刻度在”下选择自定义级别——在“值”输入自定义间距增量。 &#xff08;2&#xff09;更改小数点个数&#xff1a…
阅读更多...
嵌入式-stm32-江科大-OLED调试工具

嵌入式-stm32-江科大-OLED调试工具

文章目录 一&#xff1a;OLED调试工具1.1 OLED显示屏介绍1.2 实验&#xff1a;在OLED显示屏的使用1.3 自己新增功能测试道友&#xff1a;今天没有开始的事&#xff0c;明天绝不会完成。 一&#xff1a;OLED调试工具 1.1 OLED显示屏介绍 学习任何一门语言就需要进行调试&#…
阅读更多...
民用激光雷达行业简析

民用激光雷达行业简析

01. 激光雷达是“机器之眼” • 激光雷达是一个通过发射激光并接受发射激光同时对其进行信号处理&#xff0c;从而获得周边物体距离等信息的主动测量装置。 • 激光雷达主要由光发射、光扫描、光接收三大模块组成。光发射模块集成了驱动、开关和光源等芯片。光接收模块集成了…
阅读更多...
浏览器安装证书，使用burp抓取任意https协议的流量

浏览器安装证书，使用burp抓取任意https协议的流量

抓包显示都是http的。 接受风险后&#xff1a; 给burp加证书&#xff1a; 点击后会让你下载&#xff0c;证书已下载 证书长这个样子~~~ 浏览器设置中直接搜索证书&#xff1a; 勾选信任&#xff1a; 会到之前加载不出的页面刷新就可以看到加载出来图片等&#xff1a; 此时看到…
阅读更多...
【大数据】Flink 系统架构

【大数据】Flink 系统架构

Flink 系统架构 1.Flink 组件1.1 JobManager1.2 ResourceManager1.3 TaskManager1.4 Dispatcher 2.应用部署2.1 框架模式2.2 库模式 3.任务执行4.高可用设置4.1 TaskManager 故障4.2 JobManager 故障 Flink 是一个用于状态化并行流处理的分布式系统。它的搭建涉及多个进程&…
阅读更多...
服务器的组成

服务器的组成

服务器的重要结构组成 家用电脑组成&#xff1a; CPU、主板、内存条、显卡、硬盘、电源、风扇、网卡、显示器、机箱、键盘鼠标等等。 CPU CPU是电脑的大脑&#xff0c; CPU发展史&#xff1a; 32 位CPU&#xff1a;最大的内存寻址地址2^32&#xff0c;大约4G的大小。 CP…
阅读更多...
【基础算法练习】二分模板

【基础算法练习】二分模板

文章目录 二分模板题二分的思想C 版本的二分整数二分模板 Golang 版本的二分整数二分模板 例题&#xff1a;在排序数组中查找元素的第一个和最后一个位置题目描述C 版本代码Golang 版本代码 二分模板题 704. 二分查找&#xff0c;这道题目是最经典的二分查找&#xff0c;使用于…
阅读更多...
Git操作指南

Git操作指南

Git操作指南 Git是一款非常强大的版本控制工具&#xff0c;可以帮助开发者管理代码的版本、协同开发以及进行代码的发布。以下是一些常见的Git操作指南。 基本操作 初始化一个Git仓库 git init添加文件到暂存区 git add 文件名提交更改到本地仓库 git commit -m "提…
阅读更多...
Simulink|光伏并网逆变器低电压穿越仿真模型

Simulink|光伏并网逆变器低电压穿越仿真模型

目录 主要内容 模型研究 1.模型总览 2.boost模块 3.Inverter模块 4.控制模块 5.信号模块 结果一览 下载链接 主要内容 该模型为光伏逆变器低电压穿越仿真模型&#xff0c;采用boost加NPC拓扑结构&#xff0c;基于MATLAB/Simulink建模仿真。模型具备中点平衡…
阅读更多...
CentOS安装Redis教程-shell脚本一键安装配置

CentOS安装Redis教程-shell脚本一键安装配置

文章目录 前言一、Redis单机版安装教程1. 复制脚本2. 增加执行权限3. 执行脚本 二、Redis扩展集群版安装教程1. 安装Redis单机版2. 复制脚本3. 增加执行权限4. 执行脚本5. 测试6. redis_cluster.sh 命令6.1 启动Redis扩展集群6.2 停止Redis扩展集群6.3 查看Redis扩展集群节点信…
阅读更多...
在虚拟时空对话邓中亮院士，元宇宙访谈节目强势出圈

在虚拟时空对话邓中亮院士，元宇宙访谈节目强势出圈

​​2023年12月&#xff0c;由米果集团、浙江省元宇宙产业基地联合出品的《科技领军人物的思维模式解析》访谈节目上线。在节目制作过程中&#xff0c;主持人对话“国际欧亚科学院院士、北京邮电大学邓中亮教授”&#xff0c;全程使用蓝海创意云的“vLive虚拟直播”系统进行节目…
阅读更多...
Dubbo 3.x源码(16)—Dubbo服务发布导出源码(5)

Dubbo 3.x源码(16)—Dubbo服务发布导出源码(5)

基于Dubbo 3.1&#xff0c;详细介绍了Dubbo服务的发布与引用的源码。 此前我们学习了Dubbo 3.x源码(15)—Dubbo服务发布导出源码(4)&#xff0c;也就是Dubbo远程服务导出export方法的上半部分&#xff0c;也就是doLocalExport源码&#xff0c;将会得到一个Exporter。 现在我们…
阅读更多...
LLM之RAG理论（七）| 高提升RAG检索的四种方法

LLM之RAG理论（七）| 高提升RAG检索的四种方法

​ RAG两大核心组件&#xff1a;检索和生成。本文将总结四种提高RAG系统检索质量的技术&#xff1a;1&#xff09;子问题查询引擎&#xff08;来自LlamaIndex&#xff09;&#xff0c;2&#xff09;RAG-Fusion、3&#xff09;RAG-end2end和4&#xff09;LoRA微调。 一、L…
阅读更多...
司铭宇老师：门店经理培训：如何成为一位卓越的门店经理

司铭宇老师：门店经理培训：如何成为一位卓越的门店经理

门店经理培训&#xff1a;如何成为一位卓越的门店经理 在激烈的市场竞争中&#xff0c;门店经理作为门店的灵魂人物&#xff0c;肩负着提升门店业绩、维护品牌形象、带领团队成长等重要职责。本文将为您解析如何成为一位卓越的门店经理&#xff0c;助力您的职业生涯迈向新高峰…
阅读更多...
5个程序员可以接私活的平台和一些建议

5个程序员可以接私活的平台和一些建议

22年之前我从没有接触过程序员外包接单&#xff0c;也没有任何的私活接单经验&#xff0c;就纯纯看自己瞎摸索&#xff0c;通过Google搜索&#xff0c;在各类程序员私活接单平台上摸爬滚打&#xff0c;硬是杀出一条血路&#xff0c;从一开始的年入3k到现在每月稳定收入1w&#…
阅读更多...
【排序算法】C语言实现归并排序，包括递归和迭代两个版本

【排序算法】C语言实现归并排序，包括递归和迭代两个版本

文章目录 &#x1f680;前言&#x1f680;归并排序介绍及其思想&#x1f680;递归实现&#x1f680;迭代实现 &#x1f680;前言 大家好啊&#xff01;阿辉接着更新排序算法&#xff0c;今天要讲的是归并排序&#xff0c;这里阿辉将讲到归并排序的递归实现和迭代实现&#xff…
阅读更多...
AI服务器行业分析：预计2023年全球市场规模将达211亿美元

AI服务器行业分析：预计2023年全球市场规模将达211亿美元

AI服务器需求暴增&#xff0c;机构指出&#xff0c;AI时代浪潮汹涌&#xff0c;海量数据催生庞大的算力需求&#xff0c;带动AI服务器需求量与日俱增&#xff0c;用于服务器内、外部数据传输等接口芯片也随之攀升。 ChatGPT大火后&#xff0c;各大科技企业纷纷发力AI大模型&…
阅读更多...
Vue的生命周期方法

Vue的生命周期方法

beforeCreate 在实例初始化之后&#xff0c;数据观测&#xff08;data observe&#xff09;和 event/watcher 事件配置之前被调用。在当前阶段 data、methods、computed 以及 watch 上的数据和方法都不能被访问。 created 实例已经创建完成之后被调用。在这一步&#xff0c;实…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023