归并排序

归并排序模板题

给定你一个长度为 n 的整数数列。

请你使用归并排序对这个数列按照从小到大进行排序。

并将排好序的数列按顺序输出。

输入格式
输入共两行，第一行包含整数 n。

第二行包含 n 个整数（所有整数均在 1∼109 范围内），表示整个数列。

输出格式
输出共一行，包含 n 个整数，表示排好序的数列。

数据范围
1≤n≤100000
输入样例：
5
3 1 2 4 5
输出样例：
1 2 3 4 5

分析

归并排序采用了分治的思想，如果是第一次了解递归代码的话，可以将接下来的步骤理解为：已经将问题划分到最初始的状态，也即只是两个数的大小比较和归并。

1、有数组 q, 左端点 l, 右端点 r

2、确定划分边界 mid

3、递归处理子问题 q[l..mid], q[mid+1..r]

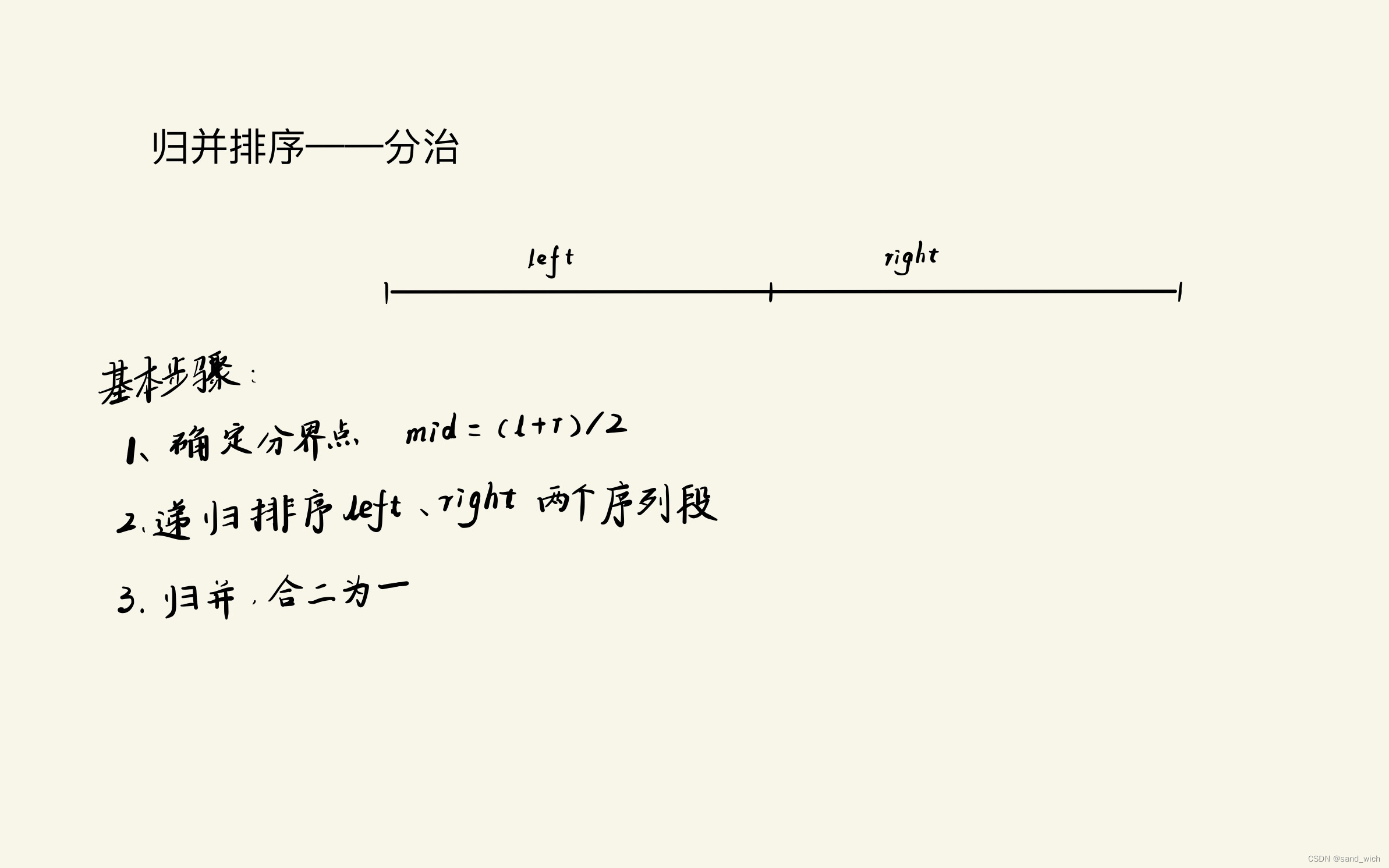
4、合并子问题

1、主体合并：至少有一个小数组添加到 tmp 数组中

2、剩余处理：可能存在的剩下的一个小数组的尾部直接添加到 tmp 数组中

3、物归原主：tmp 数组覆盖原数组

代码模板

代码尽量都写了注释，耐心看我相信一定能清楚代码是怎么得来的。

#include <iostream>


using namespace std;

const int N = 100010;

int a[N],tmp[N];

 // 归并排序
void merge_sort(int q[], int l, int r) 
{
    if (l >= r) return;

    int mid = l + r >> 1;/
    //递归 
    merge_sort(q, l, mid);
    merge_sort(q, mid + 1, r);

    int k = 0, i = l, j = mid + 1;
    //二路归并，也就是合并操作。使用两个“指针”
    while (i <= mid && j <= r)
    {
    //如果前一半的值小于后一半的值的话，将前一半的这个值放入tmp中，指针i向后挪动1位
        if (q[i] <= q[j]) tmp[k ++ ] = q[i ++ ];
        //否则指针j向后挪动一位
        else tmp[k ++ ] = q[j ++ ];
    }
    //当不满足i <= mid && j <= r后，说明有一半的已经走向了尽头，剩下的就全部放入tmp中就可以了
    while (i <= mid) tmp[k ++ ] = q[i ++ ];
    while (j <= r) tmp[k ++ ] = q[j ++ ];
    //将tmp按顺序全部放回q中
    for (i = l, j = 0; i <= r; i ++, j ++ ) q[i] = tmp[j];
}

int main()
{
    int n;
    scanf("%d", &n);
    for (int i = 0; i < n; i ++ ){
        scanf("%d", &a[i]);
    }
    merge_sort(a,0,n-1);
    
    for (int i = 0; i < n; i ++ )
        printf("%d ", a[i]);
    return 0;
}

逆序对数量统计

原理依旧是归并排序，依旧是将问题不断拆解缩小后，分为两段，首先分析左右两段，计算每一段各自的数中，是否存在逆序对，如果存在，将个数记录到res中。最后是特殊情况，将两个段放在一起进行比较，计算left段是否有数a和right段的数b组成逆序对，如果存在，则个数为mid-i+1，原因是：我们的代码是基于归并排序的，每一次递归都会进行排序，当然需要注意的是，这不会改变逆序对的数量，并且同时保证了如果存在right段的b是left段的a的逆序对，那么left段从i到mid都是b的逆序对，因此

res += mid-i+1

题目描述
给定一个长度为 n 的整数数列，请你计算数列中的逆序对的数量。

逆序对的定义如下：对于数列的第 i 个和第 j 个元素，如果满足 i<j 且 a[i]>a[j]，则其为一个逆序对；否则不是。

输入格式
第一行包含整数 n，表示数列的长度。

第二行包含 n 个整数，表示整个数列。

输出格式
输出一个整数，表示逆序对的个数。

数据范围
1≤n≤100000，
数列中的元素的取值范围 [1,109]。

输入样例：
6
2 3 4 5 6 1
输出样例：
5

#include <iostream>


using namespace std;

typedef long long LL;

const int N = 100010;

int q[N],tmp[N];


LL merge_sort(int l, int r)  // 归并排序
{
    if (l >= r) return 0;

    int mid = l + r >> 1;//从中间划分
    //结果用res存
    LL res =  merge_sort(l, mid)+merge_sort(mid + 1, r);

    //归并排序，依旧是分成两段进行比较
    int k= 0, i = l, j = mid + 1;
    //二路归并，用两个指针
    //这一次要找的是大于的位置，所以依旧是当左边小于右边时，就i++
    while (i <= mid && j <= r)
    //如果前一半的值小于后一半的值的话，将前一半的这个值放入tmp中，指针i向后挪动1位
        if (q[i] <= q[j]) tmp[k++] = q[i++];
        //否则指针j向后挪动一位，并且此时可以将res的结果得出
        //说明从i开始到mid结束的数的个数都是符合res结果的，所以res = mid -i+ 1
        else 
        {
            tmp[k++] = q[j++];
            res += mid - i + 1 ;
        } 
    //当不满足i <= mid && j <= r后，说明有一半的已经走向了尽头，剩下的就全部放入tmp中就可以了
    while(i<= mid)
        tmp[k++] = q[i++];
    while(j<= r)
        tmp[k++] = q[j++];
    //物归原主
    for (int i = l,j = 0; i <=r; i ++, j++){
        q[i] = tmp[j];
    }
    return res ;
}

int main()
{
    int n;
    //输出序列长度
    cin >> n;
    //输入序列
    for (int i = 0; i < n; i ++ ){
        cin >> q[i];
    }
    
    cout << merge_sort(0,n-1) <<endl;
    return 0;
}