实时渲染 -- 几何（Geometry）

news2024/9/30 1:42:04

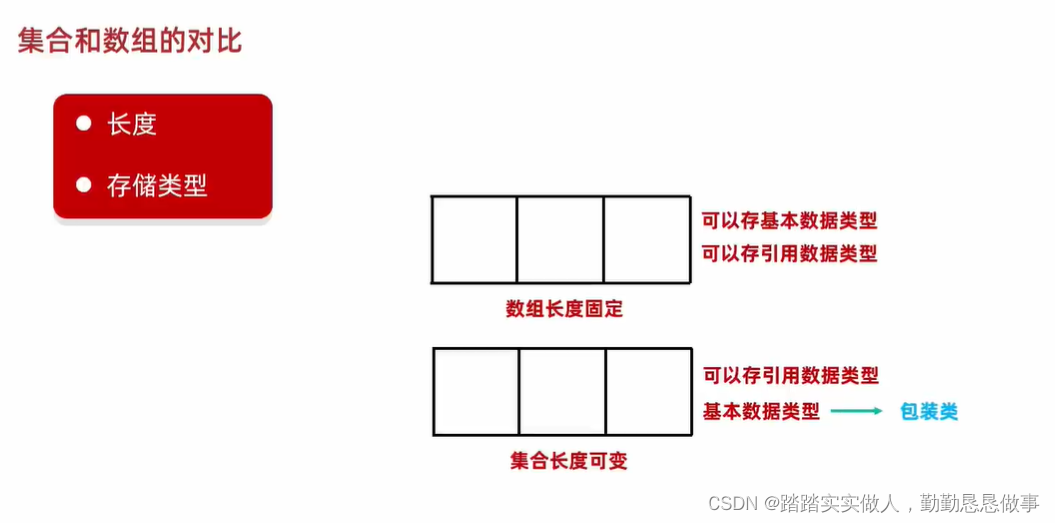
几何表示（Geometry Representation）

隐式表面（Implicit Surface）

一个函数定义一个隐式几何 f(x,y,z)=0。

容易判断一个点是在几何体内部（f<0）还是外部（f>0）

显式表面（Explicit Surface）

低维参数映射成隐式函数的高维参数。

相对容易采样，因为低维参数所需参数数量相对少了。
不容易判断点在几何体内部/外部（需要将多维参数解算成低维参数，这一步相当麻烦）。

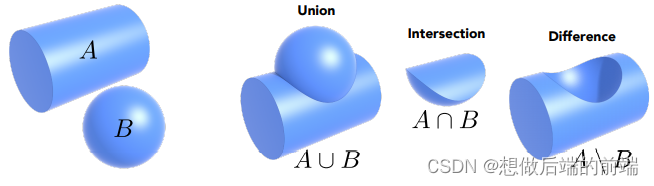
Constructive Soild Geometry

通过几何体布尔运算合成的几何体。

有向距离场（Signed Distance Field,SDF）

有向距离场（Signed Distance Field,SDF）：输入一个点，输出与这个点最近的几何体距离（有向距离）。

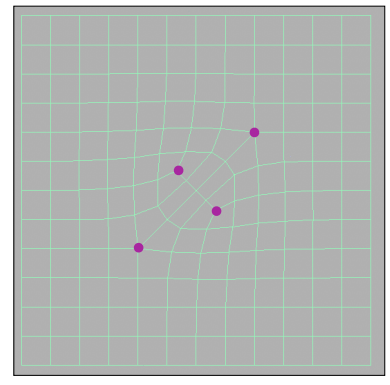
SDF 的插值会有着几何融合的效果（与一般的插值效果很不一样）：

水平集（Level Set Methods）：水平集则是一种用来表示 SDF 的存储结构，因为复杂的几何组合的 SDF 基本上很难用一个数学函数表示出来。网格存储近似函数值，坐标通过网格之间的插值可以得到函数输出。

点云（Point Cloud）

点的集合，一般涉及三维重建领域。

Polygon Mesh

渲染中最常见的几何表示法，通过存储一堆 polygons （往往是三角面 triangles，triangle 一般又有顶点和顶点索引组成）来表示一个 Polygon Mesh。

射线相交（Ray Intersection）

射线的数学形式： $r(t) = o + td (0\leq t < \infty )$

判断射线与几何函数 f(x) 的一般方法就是将射线方程代换掉 x： $f(o+td) = 0$

然后解算出 t 即为相交点，无解时则没有相交

最后还需要测试是否满足 $0\leq t < \infty$ ，即不为负数

射线与球面相交

球方程： $(x-c)^2 - R^2 = 0$

射线与平面相交

平面方程： $(x-p')\cdot N = 0$

射线与三角形相交

测试射线是否与三角形所在平面相交（若相交，将会得到相交点）
测试相交点是否在三角形内部

射线与AABB相交

轮流与各维度的两个平面做相交测试，可以预想到每个维度的测试都能获得两个解，按一大一小分类成 $t_{max},t_{min}$ 。

网格细分（Mesh Subdivision）

Loop细分算法（Loop Subdivision）

注：Loop是人名，不是循环的意思

Loop细分算法主要是针对基于三角形网格的细分。

进行一轮Loop细分的步骤：

1.先将每个三角形拆分成四个小三角形

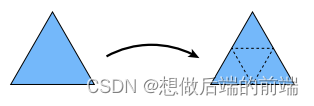
2.每个新顶点（由于三角形拆分而出现的）的位置应为：

$V_{new} = \frac{3}{8}\cdot (A+B) + \frac{1}{8}\cdot (C+D)$

其中，A、B 是新顶点所在边的两个端点（即相邻两个三角形的共享顶点），而 C、D 则分别是相邻两个三角形的非共享顶点。

3.最后，每个旧顶点的位置也应该进行调整，应为

$V'_{old} = (1-n\cdot u)\cdot V_{old} + u\cdot \sum V_{neighbor}$

注：旧顶点的位置调整并不依赖于新顶点，而是依赖于它本身和它周围的旧顶点。

其中， n 为旧顶点的度（即周围有多少个旧顶点与它直接相连），而 u�实际上代表着周围顶点的权重且有如下规则：

$u = \left\{\begin{matrix} \frac{3}{16}, & n=3\\ \frac{3}{8n}, & otherwise \end{matrix}\right.$

Loop细分效果图：

Catmull-Clack 细分算法（Catmull-Clack Subdivision）

Catmull-Clack 细分算法则是支持通用网格（如包含三角形、四边形）的细分，它的主要想法是每轮细分都在面的中心和边的中心生成新顶点，然后连接所有这些新顶点即可。

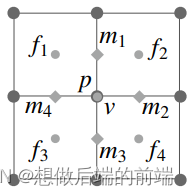
进行一轮 Catmull-Clack （针对四边形Quad Mesh的情况）细分的步骤：

1.先生成每个面的Face point： $f = \frac{v_1+v_2+v_3+v_4}{4}$

2.生成每个边的Edge point： $e = \frac{v_1+v_2+f_1+f_2}{4}$

3.调整旧顶点的位置： $v = \frac{f_1+f_2+f_3+f_4+2(m_1+m_2+m_3+m_4)+4p}{16}$

其中，m 是边的中点，p是旧顶点位置

Catmull-Clack 细分效果图：

曲面细分技术（Tessellation）

曲面细分技术（Tessellation） 通过硬件+算法的方式来完成网格细分的操作，在不耗费CPU资源的情况下让简单的模型变得细节更多、表面更加光滑。

最初，Tessellation 技术仅用于网格细分。随着DirectX11中引入可编程的Tessellation Shader后，Tessellation 技术开始多了更多的顶点插值算法来实现别的效果（例如，NVIDIA的一个Demo演示了利用Tessellation技术生产的“头发”，在有限的头发模型中镶嵌入更多的头发模型）

Tessellation 可被重新编程来用来实现如下技术（部分）：

网格细分（Mesh Subdivision）
Displacement mapping
头发镶嵌
地形渲染

在DirectX11的渲染管线中，Tessellation 技术包含了三个流程：Hull Shader、Tessellator、Domain Shader。

Hull Shader（外壳着色器）：控制自动生成顶点的数量（Tessellator的细分级别）和算法。

Tessellator：根据 Hull Shader 配置好的参数，GPU硬件会自动进行镶嵌处理。

Domain Shader（域着色器）：修改镶嵌后的顶点的属性，可用于生成曲面、法线平移、Displacement mapping等。

网格简化（Mesh Simplification）

Quadric Error 网格简化算法（Quadric Error Mesh Simplification）

1.网格简化最简单的想法是每次简化都坍缩（collapse）一条边，并且：

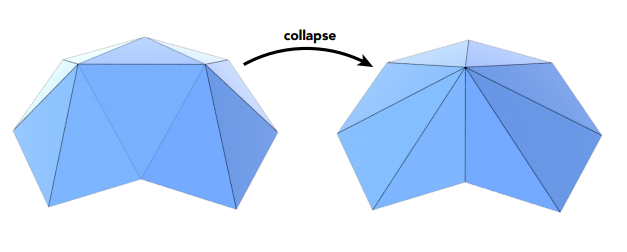
坍缩一条边后自然会形成一个新的顶点，这个顶点需要放在适当的位置来尽可能保持坍缩后的模型与原来的模型一致，于是便引入了一个衡量新旧模型差别的数值概念：Quadric Error Metrics。

朴素的想法是：新顶点位置使用取周围几个顶点的位置平均或者中点的位置，旦这样效果显然不佳（如图左）。

二次误差度量（Quadric Error Metrics）：坍缩后形成的新顶点与周围各个旧三角形所在平面的距离之和。

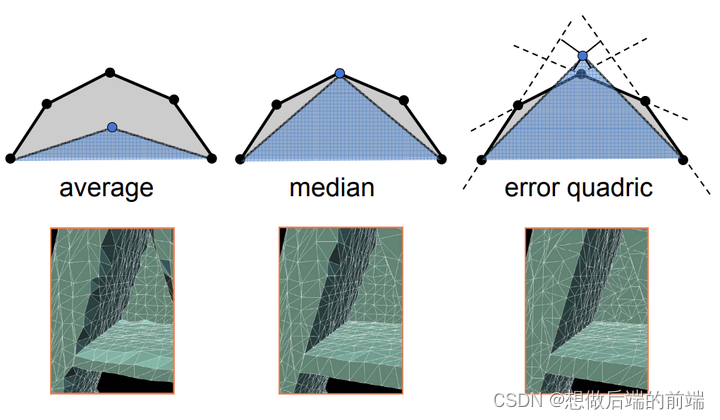
2.使用最小化 Quadric Error Metrics 方法（类比于机器学习里的最小二乘法）找到新顶点应当所在的位置即可。

Level Of Details 技术（LOD）

LOD 技术：简单来说就是渲染远处模型的时候不一定要使用原始高精度的模型，而可以使用简化的模型来替代，从而减少提交GPU的顶点数。为了做到这种优化效果且避免低模穿帮，可以根据模型与摄像机的距离来决定模型的精度（或者说简化程度）。

生成简化网格的算法往往比较耗时，因此一般采用离线计算先计算出若干个Level的模型（不同简化程度），然后在运行时根据模型与摄像机的距离来决定采用哪个Level的模型。

LOD的思想也可以应用到游戏开发的其它方面，例如一些Component的update频率可以根据与摄像机的距离来适当减小，《刺客信条》的NPC基本上就是采用这种LOD方式，因为视野远处的NPC即使行为稍有些粗糙滞后都很难被察觉到。

当然，这种Discret LOD是必然有突变的，level 切换的时候很难采用插值的方式实现模型过渡效果，因此也有LOD的实现是借助 Tessellation 技术：使用粗糙模型+Displacement mapping的方式，当模型距离最远时使用原始模型，距离越近则细分程度越高。由于细分的工作是GPU去做的，因此可以大大减少因动态切换模型而导致的开销。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1407354.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！