完整代码在最后
树结构:
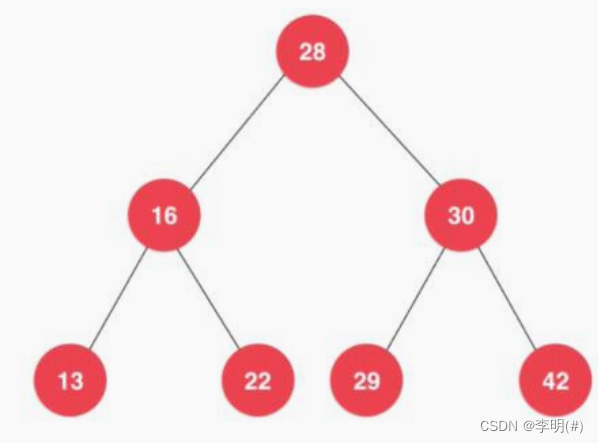
1.树结构本身是一种天然的组织结构
2.高效
二分搜索树的基础
1、二叉树
1.和链表一样:动态存储
2.具有唯一的根
3.每个结点最多只有2个孩子,每个结点最多只有一个父亲
4.具有天然的递归结构
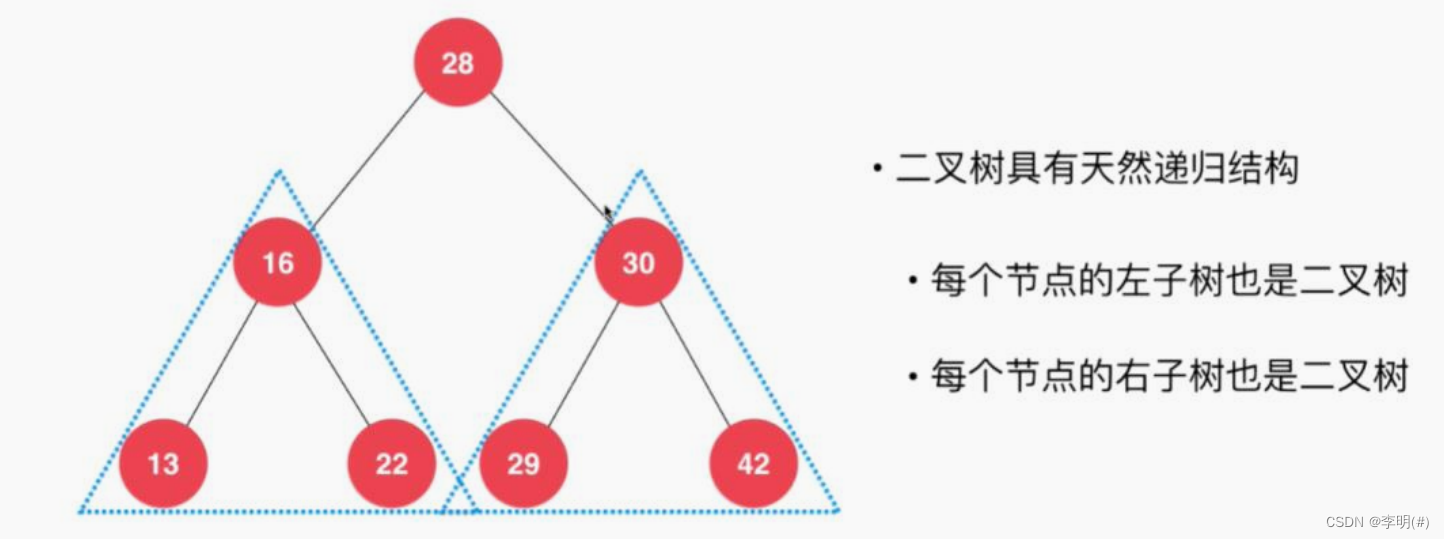
2、满二叉树
a.
叶子结点出现在二叉树的最底层,除叶子结点之外的其它结点都有两个孩子结点。
b. 一个层数为k 的满二叉树总结点数为:
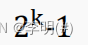
c. 第i层上的结点数为:
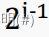
d. 一个层数为k的满二叉树的叶子结点个数(也就是最后一层):
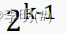
3、二叉树不一定是“满”的

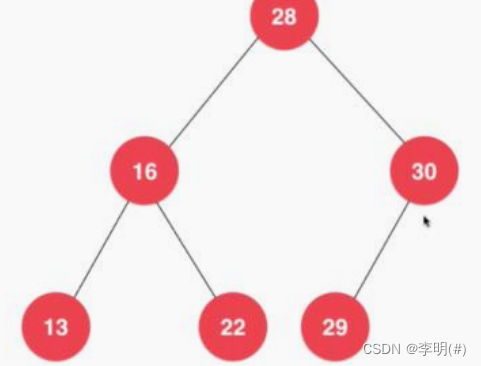
4、二分搜索树(二分排序树)
1.是二叉树
2.每个结点:大于其左子树结点值,小于右子树结点的值
3.每个子树也是二分搜索树
二分搜索树的创建和部分功能:
1.创造结点:(内部类)
//创建结点
private class Node {
private T ele;//值
private Node left;//左孩子索引
private Node right;
public Node(T ele) {
this.ele = ele;
}
}2创造树:
private Node root;//根
private int size;
public BinearySearchTree(){
this.root=null;
this.size=0;
}3.获取树结点个数:
public int getSize(){
return this.size;
}4.添加节点(递归操作)
//添加
public void add(T ele){
//更新根
this.root=addDG(this.root,ele);
this.size++;
}
//向以root为根的二分搜索树添加元素
private Node addDG(Node root,T ele){
//终止条件
if(root==null){
return new Node(ele);
}
//递归操作
if(root.ele.compareTo(ele)>0){
root.left= addDG(root.left,ele);
}
else{
root.right=addDG(root.right,ele);
}
return root;
}5.查寻值是否存在(递归操作)
//查询
public boolean search(T ele){
return searchDG(this.root,ele);
}
private boolean searchDG(Node root,T ele){
//终止
if(root==null){
return false;
}
if(root.ele.compareTo(ele)==0){
return true;
}else if(root.ele.compareTo(ele)>0){
return searchDG(root.left,ele);
}else{
return searchDG(root.right,ele);
}
}6.遍历(先序,中序,后续)
先序:
public void preTravel() {
//先序
List<T> list = new ArrayList<>();
preTrvelDG(this.root, list);
String res=list.stream().map(item -> item.toString()).collect(Collectors.joining("-"));
System.out.println(res);
}
private void preTrvelDG(Node root,List<T>list){
//先序
if(root==null){
//判断
return ;
}
//操作
list.add(root.ele);
preTrvelDG(root.left,list);
preTrvelDG(root.right,list);
}中序:
public void midTravel() {
//中序
List<T> list = new ArrayList<>();
midTrvelDG(this.root, list);
String res=list.stream().map(item -> item.toString()).collect(Collectors.joining("-"));
System.out.println(res);
}
private void midTrvelDG(Node root,List<T>list){
//中序
if(root==null){
//判断
return ;
}
//操作
midTrvelDG(root.left,list);
list.add(root.ele);
midTrvelDG(root.right,list);
}后续
public void suffiuxTravel() {
//后序
List<T> list = new ArrayList<>();
suffiuxTrvelDG(this.root, list);
String res=list.stream().map(item -> item.toString()).collect(Collectors.joining("-"));
System.out.println(res);
}
private void suffiuxTrvelDG(Node root,List<T>list){
//后序
if(root==null){
//判断
return ;
}
//操作
suffiuxTrvelDG(root.left,list);
suffiuxTrvelDG(root.right,list);
list.add(root.ele);
}
7.完整代码
package com.ffyc.learn.binearysearch;
import com.ffyc.leetcodetest.sortList077;
import java.util.ArrayList;
import java.util.List;
import java.util.Random;
import java.util.stream.Collectors;
//二分搜索树
public class BinearySearchTree<T extends Comparable<T>> {
//创建结点
private class Node {
private T ele;//值
private Node left;//左孩子索引
private Node right;
public Node(T ele) {
this.ele = ele;
}
}
private Node root;//根
private int size;
public BinearySearchTree(){
this.root=null;
this.size=0;
}
public int getSize(){
return this.size;
}
//添加
public void add(T ele){
//更新根
this.root=addDG(this.root,ele);
this.size++;
}
//向以root为根的二分搜索树添加元素
private Node addDG(Node root,T ele){
//终止条件
if(root==null){
return new Node(ele);
}
//递归操作
if(root.ele.compareTo(ele)>0){
root.left= addDG(root.left,ele);
}
else{
root.right=addDG(root.right,ele);
}
return root;
}
//查询
public boolean search(T ele){
return searchDG(this.root,ele);
}
private boolean searchDG(Node root,T ele){
//终止
if(root==null){
return false;
}
if(root.ele.compareTo(ele)==0){
return true;
}else if(root.ele.compareTo(ele)>0){
return searchDG(root.left,ele);
}else{
return searchDG(root.right,ele);
}
}
//遍历
public void preTravel() {
//先序
List<T> list = new ArrayList<>();
preTrvelDG(this.root, list);
String res=list.stream().map(item -> item.toString()).collect(Collectors.joining("-"));
System.out.println(res);
}
private void preTrvelDG(Node root,List<T>list){
//先序
if(root==null){
//判断
return ;
}
//操作
list.add(root.ele);
preTrvelDG(root.left,list);
preTrvelDG(root.right,list);
}
public void midTravel() {
//中序
List<T> list = new ArrayList<>();
midTrvelDG(this.root, list);
String res=list.stream().map(item -> item.toString()).collect(Collectors.joining("-"));
System.out.println(res);
}
private void midTrvelDG(Node root,List<T>list){
//中序
if(root==null){
//判断
return ;
}
//操作
midTrvelDG(root.left,list);
list.add(root.ele);
midTrvelDG(root.right,list);
}
public void suffiuxTravel() {
//后序
List<T> list = new ArrayList<>();
suffiuxTrvelDG(this.root, list);
String res=list.stream().map(item -> item.toString()).collect(Collectors.joining("-"));
System.out.println(res);
}
private void suffiuxTrvelDG(Node root,List<T>list){
//后序
if(root==null){
//判断
return ;
}
//操作
suffiuxTrvelDG(root.left,list);
suffiuxTrvelDG(root.right,list);
list.add(root.ele);
}
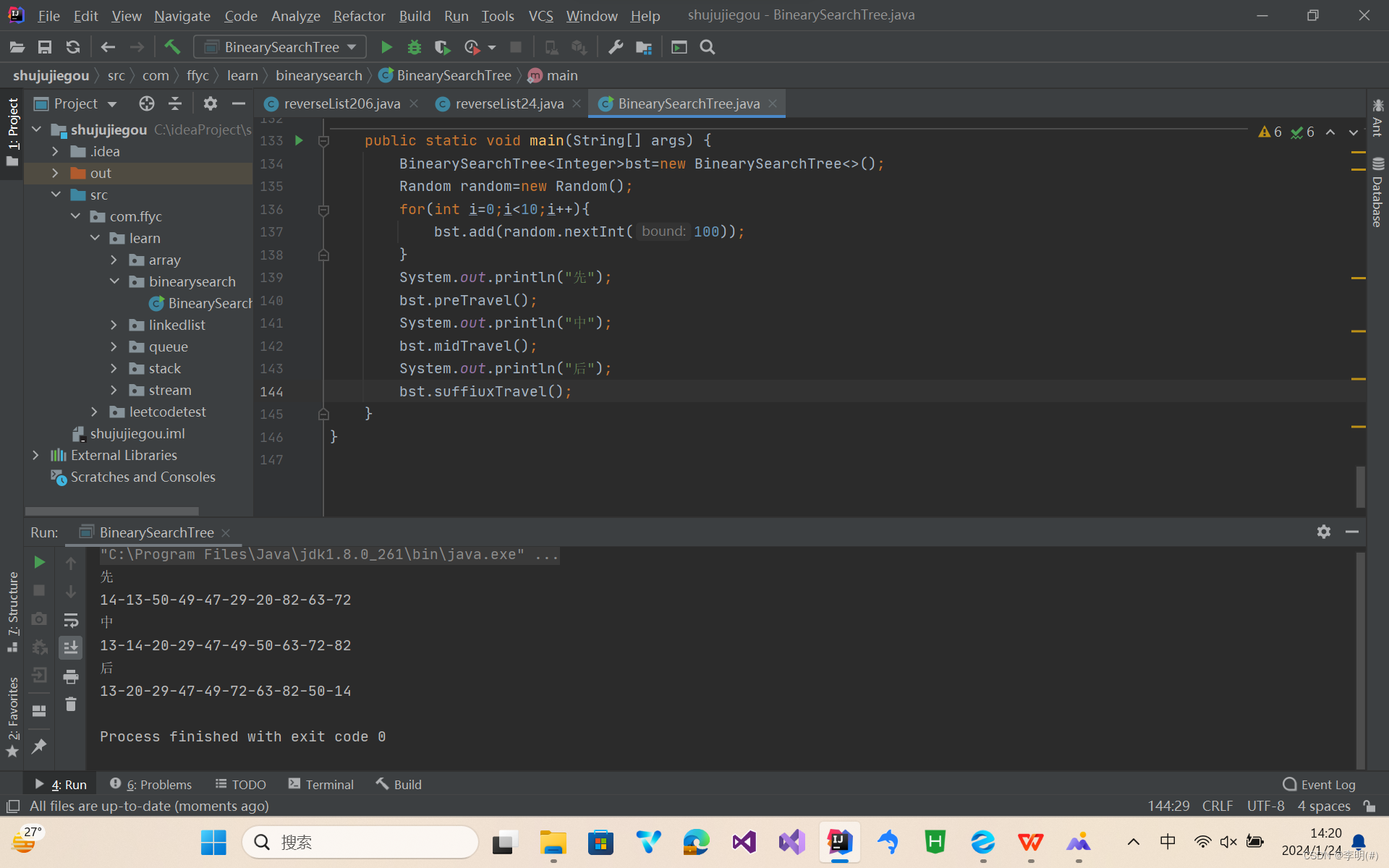
public static void main(String[] args) {
BinearySearchTree<Integer>bst=new BinearySearchTree<>();
Random random=new Random();
for(int i=0;i<10;i++){
bst.add(random.nextInt(100));
}
System.out.println("先");
bst.preTravel();
System.out.println("中");
bst.midTravel();
System.out.println("后");
bst.suffiuxTravel();
}
}
8.测试结果: