论文：Feature Pyramid Networks for Object Detection （CVPR 2016)
参考blog：https://blog.csdn.net/weixin_55073640/article/details/122627966
参考视频讲解：添加链接描述

卷积网络中，深层网络容易响应语义特征，浅层网络容易响应图像特征。然而，在目标检测中往往因为卷积网络的这个特征带来了不少麻烦：

高层网络虽然能响应语义特征，但是由于Feature Map的尺寸太小，拥有的几何信息并不多，不利于目标的检测；浅层网络虽然包含比较多的几何信息，但是图像的语义特征并不多，不利于图像的分类。这个问题在小目标检测中更为突出。
为何可以处理小目标问题：

1. FPN可以利用经过top-down模型后的那些上下文信息（高层语义信息）；
2. 对于小目标而言，FPN增加了特征映射的分辨率（即在更大的feature map上面进行操作，这样可以获得更多关于小目标的有用信息）。

FPN图示

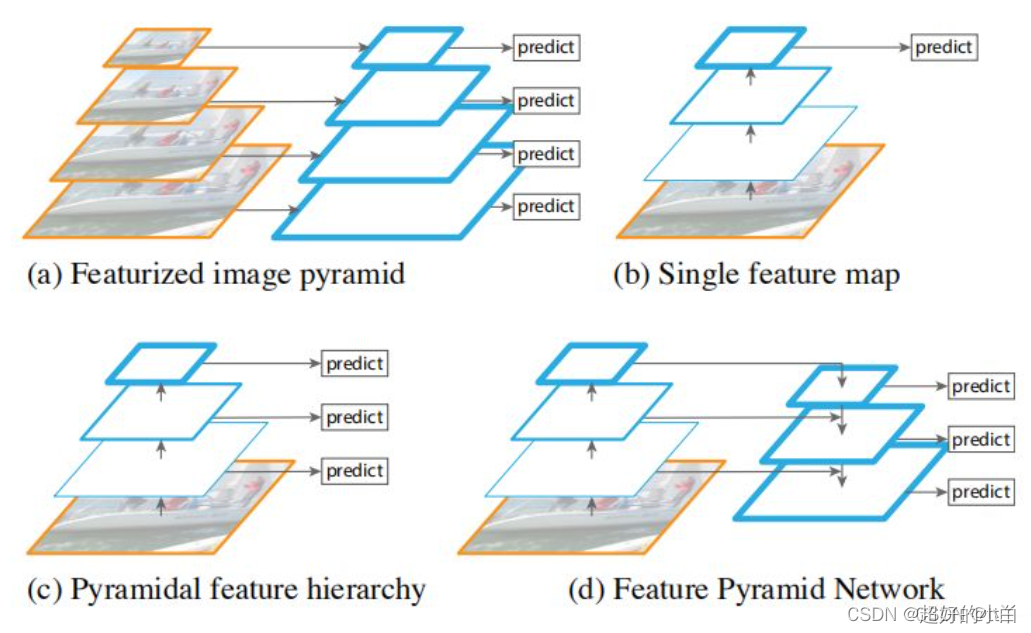图（a）：

先对原始图像构造图像金字塔，然后在图像金字塔的每一层提出不同的特征，然后进行相应的预测。优点：精度不错；缺点：计算量大得恐怖，占用内存大。直接pass！

图（b）：

通过对原始图像进行卷积和池化操作来获得不同尺寸的feature map，在图像的特征空间中构造出金字塔。

因为浅层的网络更关注于细节信息，高层的网络更关注于语义信息，更有利于准确检测出目标，因此利用最后一个卷积层上的feature map来进行预测分类。

优点：速度快、内存少。缺点：仅关注深层网络中最后一层的特征，却忽略了其它层的特征。

图（c）：

同时利用低层特征和高层特征。就是首先在原始图像上面进行深度卷积，然后分别在不同的特征层上面进行预测。

优点：在不同的层上面输出对应的目标，不需要经过所有的层才输出对应的目标（即对于有些目标来说，不用进行多余的前向操作），速度更快，又提高了算法的检测性能。

缺点：获得的特征不鲁棒，都是一些弱特征（因为很多的特征都是从较浅的层获得的）。
图（d）这才是我们真正的FPN

简单概括来说就是：自下而上，自上而下，横向连接和卷积融合。

整体过程：

（1）自下而上：先把预处理好的图片送进预训练的网络，比如像ResNet这些，这一步就是构建自下而上的网络，就是对应下图中的（1，2，3）这一组金字塔。

（2）自上而下：将层3进行一个复制变成层4，对层4进行上采样操作（就是2 * up），再用1 * 1卷积对层2进行降维处理，然后将两者对应元素相加（这里就是高低层特征的一个汇总），这样我们就得到了层5，层6以此类推，是由层5和层1进行上述操作得来的。这样就构成了自上而下网络，对应下图（4，5，6）金字塔。（其中的层2与上采样后的层4进行相加，就是横向连接的操作）

（3）卷积融合：最后我们对层4，5，6分别来一个3 * 3卷积操作得到最终的预测（对应下图的predict）。

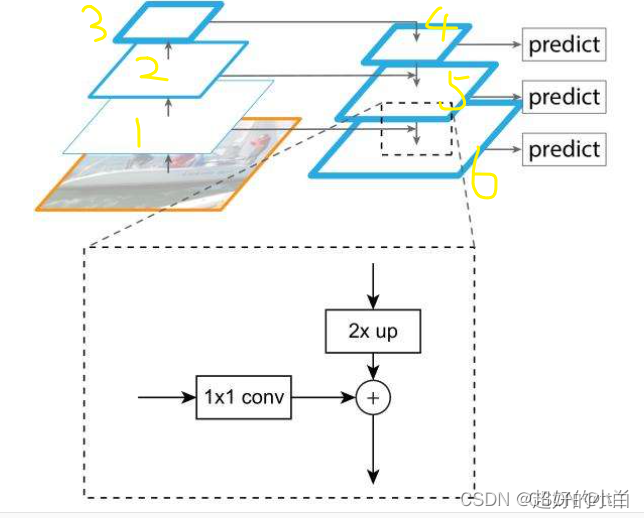
FPN细节结构示例