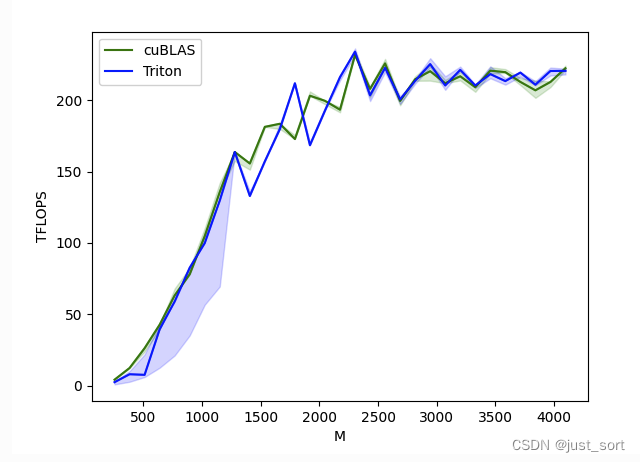
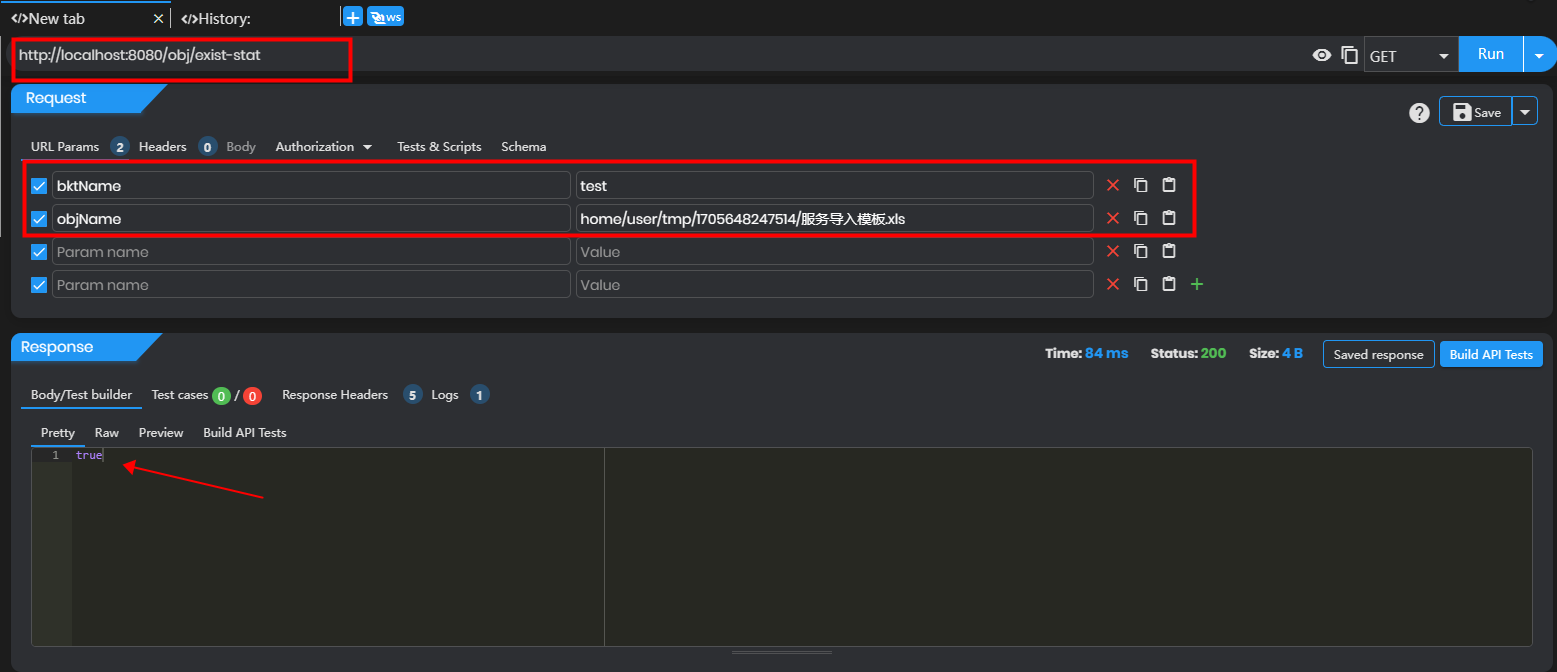
Actor-Critic算法结合了策略梯度和值函数的优点,我们将其分为两部分,Actor(策略网络)和Critic(价值网络)
- Actor与环境交互,在Critic价值函数的指导下使用策略梯度学习好的策略
- Critic通过Actor与环境交互收集的数据学习,得到一个价值函数,来判断当前状态哪些动作是好,哪些动作是坏,进而帮Actor进行策略更新。

A2C算法
AC算法的目的是为了消除策略梯度算法的高仿查问题,可以引用优势函数(advantage function)
A
π
(
s
t
,
a
t
)
A^{\pi}(s_t,a_t)
Aπ(st,at) ,来表示当前当前状态-动作对相对于平均水平的优势:
A
π
(
s
t
,
a
t
)
=
Q
π
(
s
t
,
a
t
)
−
V
π
(
s
t
)
A^{\pi}(s_t,a_t)=Q^{\pi}(s_t,a_t)-V^{\pi}(s_t)
Aπ(st,at)=Qπ(st,at)−Vπ(st)
通过与平均水平相减,可以降低方差。但需要注意的是,相减的是
V
π
(
s
t
)
V^{\pi}(s_t)
Vπ(st) ,即在状态
s
t
s_t
st 下的价值,即状态
s
t
s_t
st 的回报的均值,而不是所有状态
s
s
s 的回报的均值。
可以将目标函数改为:
∇
θ
J
(
θ
)
∝
E
π
θ
[
A
π
(
s
t
,
a
t
)
∇
θ
log
π
θ
(
a
t
∣
s
t
)
]
\nabla_\theta J(\theta)\propto\mathbb{E}_{\pi_\theta}\left[A^\pi(s_t,a_t)\nabla_\theta\log\pi_\theta(a_t\mid s_t)\right]
∇θJ(θ)∝Eπθ[Aπ(st,at)∇θlogπθ(at∣st)]
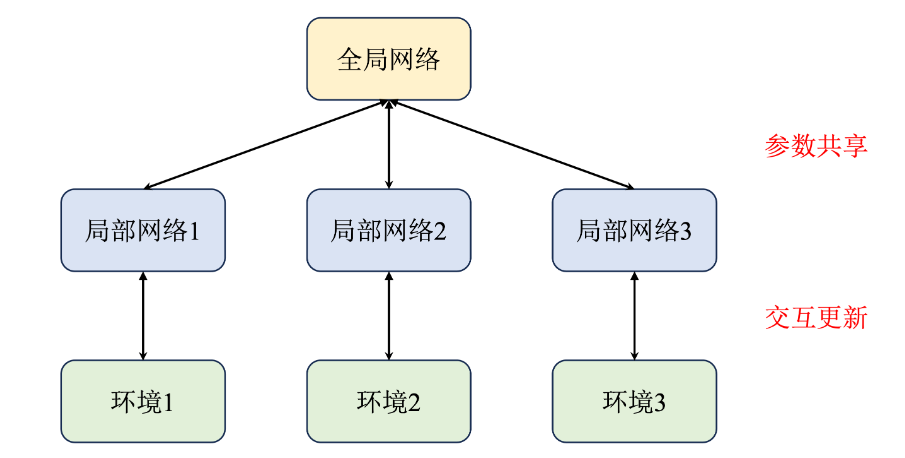
这就是A2C算法(Advantage Actor-Critic)算法。脱胎于A3C算法,即增加了多个进程,每一个进程都拥有一个独立的网络和环境以供训练。
广义优势估计
时序差分能有效解决高方差问题但是是有偏估计,而蒙特卡洛是无偏估计但是会带来高方差问题,因此通常会结合这两个方法形成一种新的估计方式,即 T D ( λ ) TD(\lambda) TD(λ) 估计,通过结合多步,形成新的估计方式,成为广义优势估计(generalized advantage estimation GAE)。
A
GAE
(
γ
,
λ
)
(
s
t
,
a
t
)
=
∑
l
=
0
∞
(
γ
λ
)
l
δ
t
+
l
=
∑
l
=
0
∞
(
γ
λ
)
l
(
r
t
+
l
+
γ
V
π
(
s
t
+
l
+
1
)
−
V
π
(
s
t
+
l
)
)
\begin{aligned} A^{\text{GAE}(\gamma,\lambda)}(s_t,a_t)& =\sum_{l=0}^\infty(\gamma\lambda)^l\delta_{t+l} \\ &=\sum_{l=0}^\infty(\gamma\lambda)^l\left(r_{t+l}+\gamma V^\pi(s_{t+l+1})-V^\pi(s_{t+l})\right) \end{aligned}
AGAE(γ,λ)(st,at)=l=0∑∞(γλ)lδt+l=l=0∑∞(γλ)l(rt+l+γVπ(st+l+1)−Vπ(st+l))
其中,
δ
t
+
l
\delta_{t+l}
δt+l 为时步
t
+
l
t+l
t+l 的TD误差,为:
δ
t
+
l
=
r
t
+
l
+
γ
V
π
(
s
t
+
l
+
1
)
−
V
π
(
s
t
+
l
)
\delta_{t+l}=r_{t+l}+\gamma V^{\pi}(s_{t+l+1})-V^{\pi}(s_{t+l})
δt+l=rt+l+γVπ(st+l+1)−Vπ(st+l)
当
λ
=
0
\lambda=0
λ=0 时,退化为单步TD误差:
A
G
A
E
(
γ
,
0
)
(
s
t
,
a
t
)
=
δ
t
=
r
t
+
γ
V
π
(
s
t
+
1
)
−
V
π
(
s
t
)
A^{\mathrm{GAE}(\gamma,0)}(s_t,a_t)=\delta_t=r_t+\gamma V^\pi(s_{t+1})-V^\pi(s_t)
AGAE(γ,0)(st,at)=δt=rt+γVπ(st+1)−Vπ(st)
当
λ
=
1
\lambda=1
λ=1 时,则为蒙特卡洛估计:
A
G
A
E
(
γ
,
1
)
(
s
t
,
a
t
)
=
∑
l
=
0
∞
(
γ
λ
)
l
δ
t
+
l
=
∑
l
=
0
∞
(
γ
)
l
δ
t
+
l
A^{\mathrm{GAE}(\gamma,1)}(s_t,a_t)=\sum_{l=0}^\infty(\gamma\lambda)^l\delta_{t+l}=\sum_{l=0}^\infty(\gamma)^l\delta_{t+l}
AGAE(γ,1)(st,at)=l=0∑∞(γλ)lδt+l=l=0∑∞(γ)lδt+l
代码实操

import gymnasium as gym
import torch
import torch.nn.functional as F
import numpy as np
import matplotlib.pyplot as plt
import rl_utils
# 定义策略网络
class PolicyNet(torch.nn.Module):
def __init__(self, state_dim, hidden_dim, action_dim):
super(PolicyNet, self).__init__()
self.fc1 = torch.nn.Linear(state_dim, hidden_dim)
self.fc2 = torch.nn.Linear(hidden_dim, action_dim)
def forward(self, x):
x = F.relu(self.fc1(x))
return F.softmax(self.fc2(x), dim=1)
# 定义价值网络,输出一个价值,为一维张量
class ValueNet(torch.nn.Module):
def __init__(self, state_dim, hidden_dim):
super(ValueNet, self).__init__()
self.fc1 = torch.nn.Linear(state_dim, hidden_dim)
self.fc2 = torch.nn.Linear(hidden_dim, 1)
def forward(self, x):
x = F.relu(self.fc1(x))
return self.fc2(x)
现在定义A2C算法的主题,包括采取动作和更新网络参数的两个函数。
class ActorCritic:
def __init__(self, state_dim, hidden_dim, action_dim, actor_lr, critic_lr,
gamma, device):
# 策略网络
self.actor = PolicyNet(state_dim, hidden_dim, action_dim).to(device)
self.critic = ValueNet(state_dim, hidden_dim).to(device) # 价值网络
# 策略网络优化器
self.actor_optimizer = torch.optim.Adam(self.actor.parameters(),
lr=actor_lr)
self.critic_optimizer = torch.optim.Adam(self.critic.parameters(),
lr=critic_lr) # 价值网络优化器
self.gamma = gamma
self.device = device
def take_action(self, state):
state = torch.tensor([state], dtype=torch.float).to(self.device)
probs = self.actor(state)
action_dist = torch.distributions.Categorical(probs)
action = action_dist.sample()
return action.item()
def update(self,transition_dict):
states = torch.tensor(transition_dict['states'],
dtype=torch.float).to(self.device)
actions = torch.tensor(transition_dict['actions']).view(-1, 1).to(
self.device)
rewards = torch.tensor(transition_dict['rewards'],
dtype=torch.float).view(-1, 1).to(self.device)
next_states = torch.tensor(transition_dict['next_states'],
dtype=torch.float).to(self.device)
dones = torch.tensor(transition_dict['dones'],
dtype=torch.float).view(-1, 1).to(self.device)
# 时序差分目标
td_target=rewards+self.gamma*self.critic(next_states)*(1-dones)
# 进行时序擦划分
td_delta=td_target-self.critic(states)
log_probs=torch.log(self.actor(states).gather(1,actions))
actor_loss=torch.mean(-log_probs*td_delta.detach())
# 均方误差损失函数
critic_loss = torch.mean(F.mse_loss(self.critic(states), td_target.detach()))
self.actor_optimizer.zero_grad()
self.critic_optimizer.zero_grad()
actor_loss.backward() # 计算策略网络的梯度
critic_loss.backward() # 计算价值网络的梯度
self.actor_optimizer.step() # 更新策略网络的参数
self.critic_optimizer.step() # 更新价值网络的参数
actor_lr = 1e-3
critic_lr = 1e-2
num_episodes = 1000
hidden_dim = 128
gamma = 0.98
device = torch.device("cuda") if torch.cuda.is_available() else torch.device(
"cpu")
env_name = 'CartPole-v0'
env = gym.make(env_name)
torch.manual_seed(0)
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.n
agent = ActorCritic(state_dim, hidden_dim, action_dim, actor_lr, critic_lr,
gamma, device)
return_list = rl_utils.train_on_policy_agent(env, agent, num_episodes)
episodes_list = list(range(len(return_list)))
plt.plot(episodes_list, return_list)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('Actor-Critic on {}'.format(env_name))
plt.show()
mv_return = rl_utils.moving_average(return_list, 9)
plt.plot(episodes_list, mv_return)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('Actor-Critic on {}'.format(env_name))
plt.show()
state = torch.tensor([state], dtype=torch.float).to(self.device)
Iteration 0: 100%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 100/100 [00:03<00:00, 25.55it/s, episode=100, return=20.400]
Iteration 1: 100%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 100/100 [00:04<00:00, 24.48it/s, episode=200, return=51.200]
Iteration 2: 100%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 100/100 [00:14<00:00, 6.91it/s, episode=300, return=151.500]
Iteration 3: 100%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 100/100 [00:25<00:00, 3.88it/s, episode=400, return=256.700]
Iteration 4: 53%|███████████████████████████████████████████████████████████████████████████████▌ | 53/100 [00:17<00:10, 4.51it/s, episode=450, return=235.500]