目录
1.根据二叉树创建字符串
2.二叉树的层序遍历
3.二叉树的层序遍历2
4.二叉树的最近公共祖先
5. 搜索二叉树与双向链表
6.从前序与中序遍历构建二叉树
1.根据二叉树创建字符串
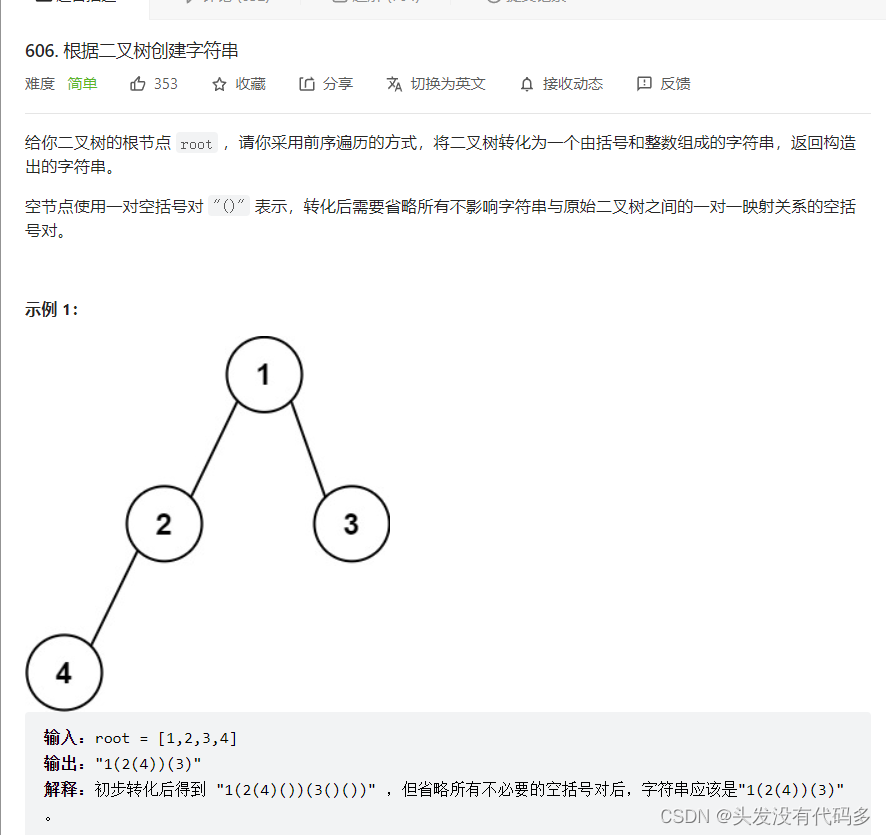
按照前序遍历:根左右。
1(2(4()())())(3()())
1.左右都为空,则可以省略掉括号
如这里的3,还有4 1(2(4)())(3)
2.左子树不为空,右子树为空,省略掉
如2,1(2(4))(3)
3.如果左为空。不省略
class Solution { public: string tree2str(TreeNode* root) { if(root==nullptr) return string(); string str; str+=to_string(root->val);//根节点 if(root->left||root->right) //左边不为空或者左边为空右边不为空,左边需要加括号 { str+='('; //左子树 str+=tree2str(root->left); str+=')'; } if(root->right)//右边不为空,则加括号 { str+='('; //右子树 str+=tree2str(root->right); str+=')'; } return str; } };
2.二叉树的层序遍历
102. 二叉树的层序遍历 - 力扣(LeetCode)
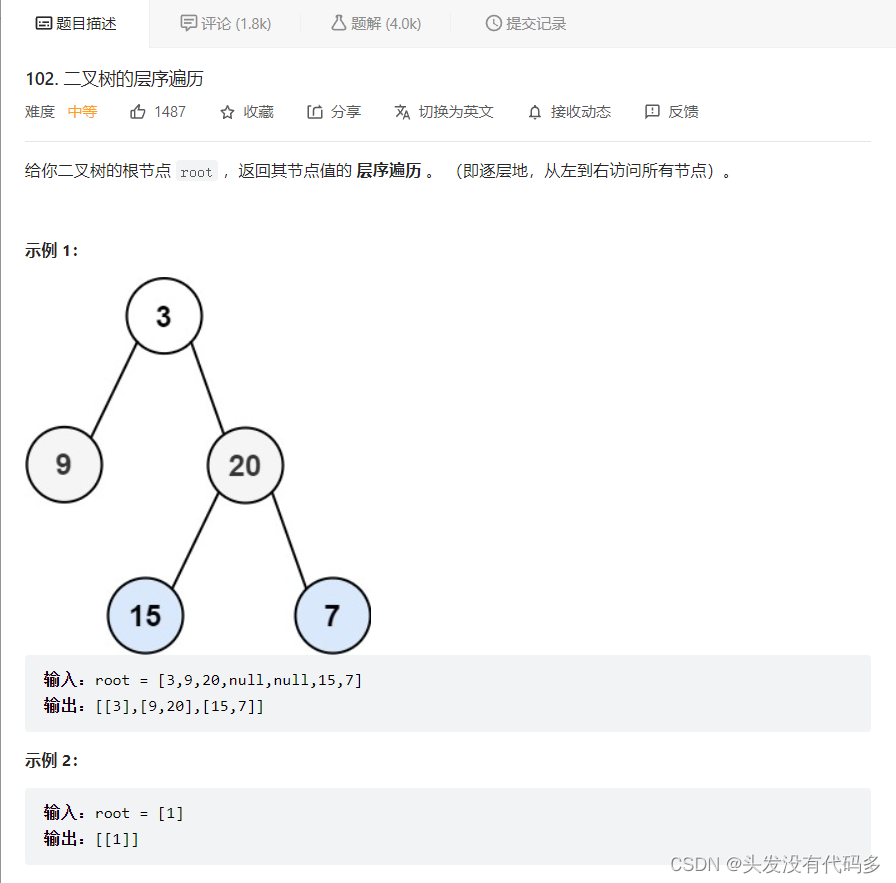
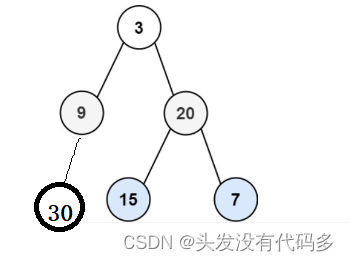
思路:使用队列,当某个节点出来的时候,将他的子节点放入
9出来后放入30,但有个问题,不知道每一层的分界点在哪 ,这里当20出来后不知道30是这一场的还是下一层的
解决办法:用一个数字去记录每层的个数,控制一层一层出
class Solution { public: vector<vector<int>> levelOrder(TreeNode* root) { queue<TreeNode*> q; size_t levelSize=0; if(root) { q.push(root); levelSize=1; } vector<vector<int>> vv; while(!q.empty()) { vector<int> v; for(size_t i=0;i<levelSize;++i) { TreeNode*front=q.front(); q.pop(); v.push_back(front->val); if(front->left) q.push(front->left); if(front->right) q.push(front->right); } vv.push_back(v);//把这一层给v levelSize=q.size(); } return vv; } };
3.二叉树的层序遍历2
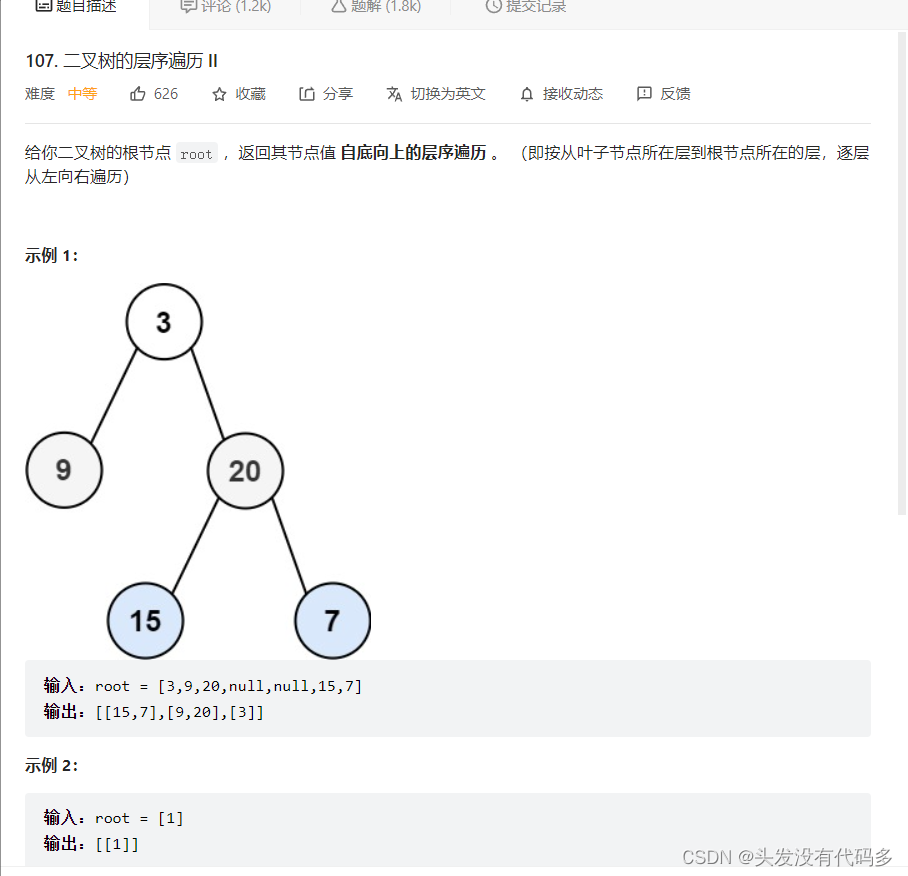
107. 二叉树的层序遍历 II - 力扣(LeetCode)
逆置一下即可
class Solution { public: vector<vector<int>> levelOrderBottom(TreeNode* root) { queue<TreeNode*> q; size_t levelSize=0; if(root) { q.push(root); levelSize=1; } vector<vector<int>> vv; while(!q.empty()) { vector<int> v; for(size_t i=0;i<levelSize;++i) { TreeNode*front=q.front(); q.pop(); v.push_back(front->val); if(front->left) q.push(front->left); if(front->right) q.push(front->right); } vv.push_back(v);//把这一层给v levelSize=q.size(); } reverse(vv.begin(),vv.end()); return vv; } };
4.二叉树的最近公共祖先
236. 二叉树的最近公共祖先 - 力扣(LeetCode)
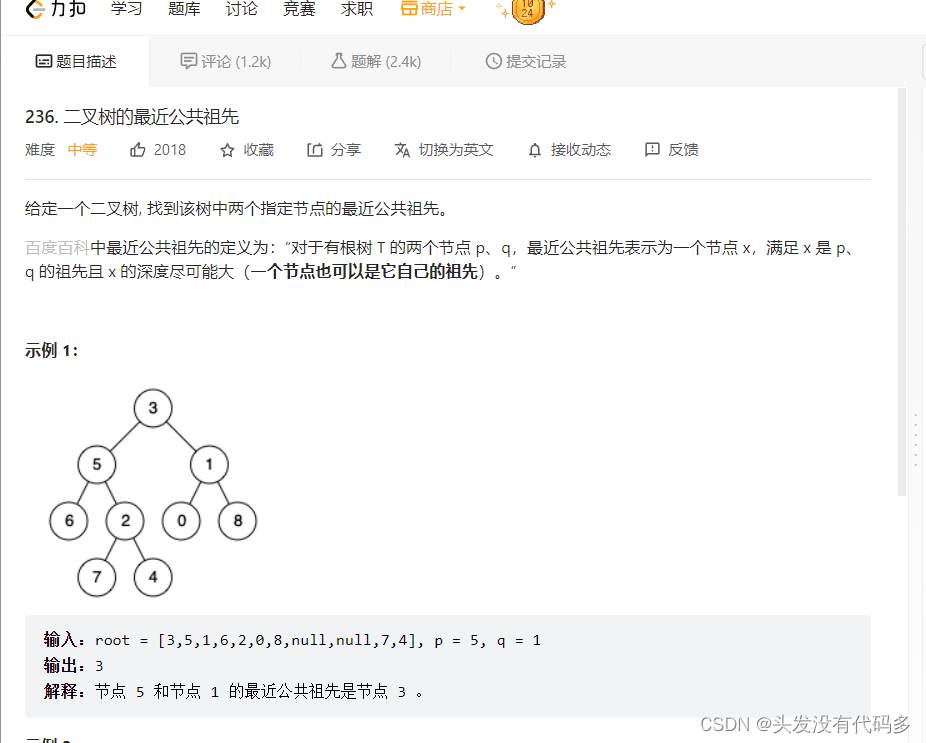
思路:如果一个是某节点左子树中的节点,一个是它右子树中的节点,该节点就是公共祖先
//1.一个在左,一个在右,root是公共祖先
//2.都在左,递归到左子树找
//3.都在右,递归到右子树找class Solution { public: bool Find(TreeNode *sub,TreeNode *x) { if(sub==nullptr) return false; if(sub==x) return true; return sub==x||Find(sub->left,x) ||Find(sub->right,x); } TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) { if(root==nullptr) return nullptr; if(root==p||root==q)//如果p或q是根节点,就说明root是公共祖先 { return root; } bool pInleft,pInright,qInleft,qInright; pInleft=Find(root->left,p);//在左子树中去找p pInright=!pInleft; qInleft=Find(root->left,q);//在右子树中去找q qInright=!qInleft; //1.一个在左,一个在右,root是公共祖先 //2.都在左,递归到左子树找 //3.都在右,递归到右子树找 if((pInleft&&qInright)||(qInleft&&pInright)) return root; else if(pInleft&&qInleft)//如果都在左 { return lowestCommonAncestor(root->left,p,q); } else if(pInright&&qInright)//如果都在左 { return lowestCommonAncestor(root->right,p,q); } else return nullptr; } };时间复杂度是O(H*N),H是树的高度,我们将时间复杂度优化到O(N)
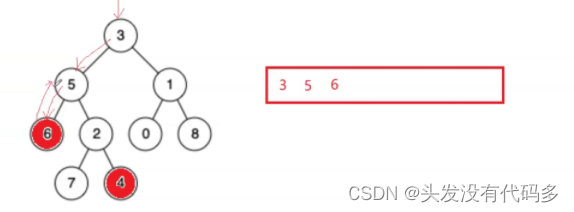
使用一个栈解决,如果不是我们要找的节点就入栈,如这里要找6,4把往6这条路走的节点都入栈。之后返回。
这里找4,先找左数3,5,6 6的左右子树为空,就说明没找到4,把6出栈
.
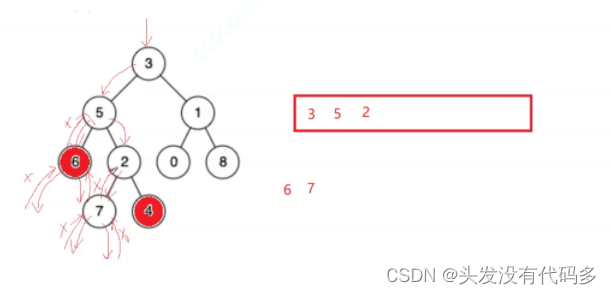
出栈之后从2开始找,从左子树开始找,再找右子树
此时有俩个栈
我们让大的栈先pop,先pop4,然后比较2和6不相等pop2和6,再比较5和5相等就说明找到了
class Solution { public: bool FindPath(TreeNode *root,TreeNode* x, stack<TreeNode*>&path) { if(root==nullptr) return false; path.push(root);//先入栈 if(root==x) return true;//找到了该节点 if(FindPath(root->left,x,path))//如果没找到就去左数找 return true;//左树找到了就返回 if(FindPath(root->right,x,path))//左树没找到就去右树找 return true; path.pop();//左边右边都没找到pop出去该节点 return false;//左右都没找到 } TreeNode *lowestCommonAncestor(TreeNode *root,TreeNode *p,TreeNode *q) { stack<TreeNode*>pPath,qPath; FindPath(root,p,pPath); FindPath(root,q,qPath); //类似链表相交,长的先走 while(pPath.size()!=qPath.size()) { if(pPath.size()>qPath.size()) pPath.pop(); else qPath.pop(); } while(pPath.top()!=qPath.top()) { pPath.pop(); qPath.pop(); } return pPath.top(); } };
5. 搜索二叉树与双向链表
二叉搜索树与双向链表_牛客题霸_牛客网 (nowcoder.com)
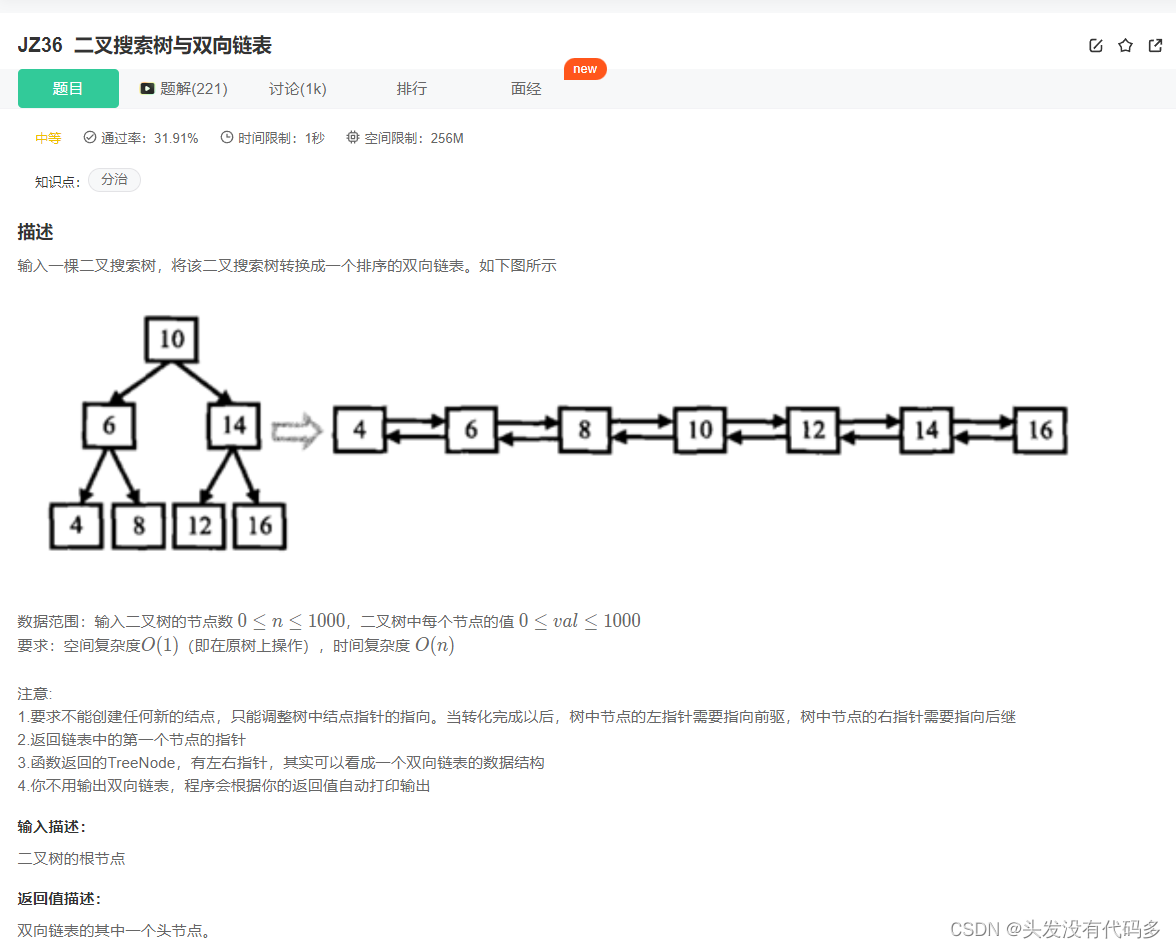
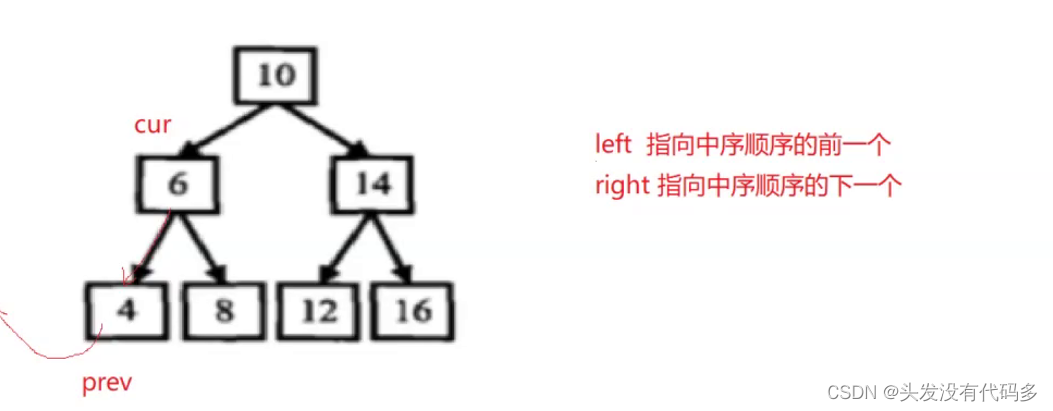
中序递归遍历,这里让left指向中序顺序的前一个,right指向中序顺序的下一个
用俩个指针prev和cur,cur比prev先走一步。
走到这时让cur->left指向prev
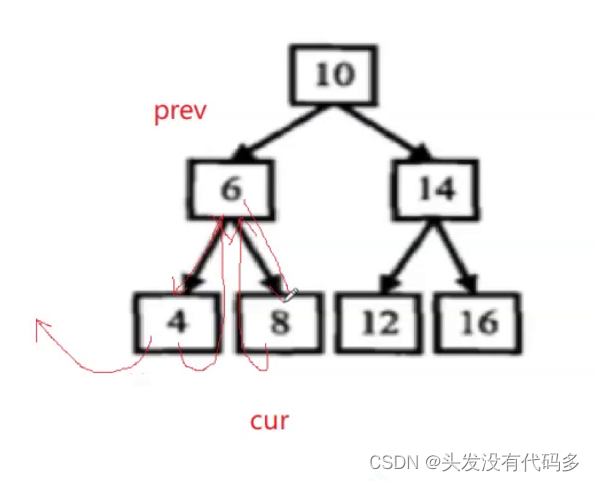
由于是中序遍历,cur走到6之后会走到8,让8的left指向6
解决了left,接下来解决right,right要指向下一个即4->6->8->10
换个遍历顺序:右->根->左这样可以处理右节点
还下面这种办法,让prev的右指向6
让6的右指向8
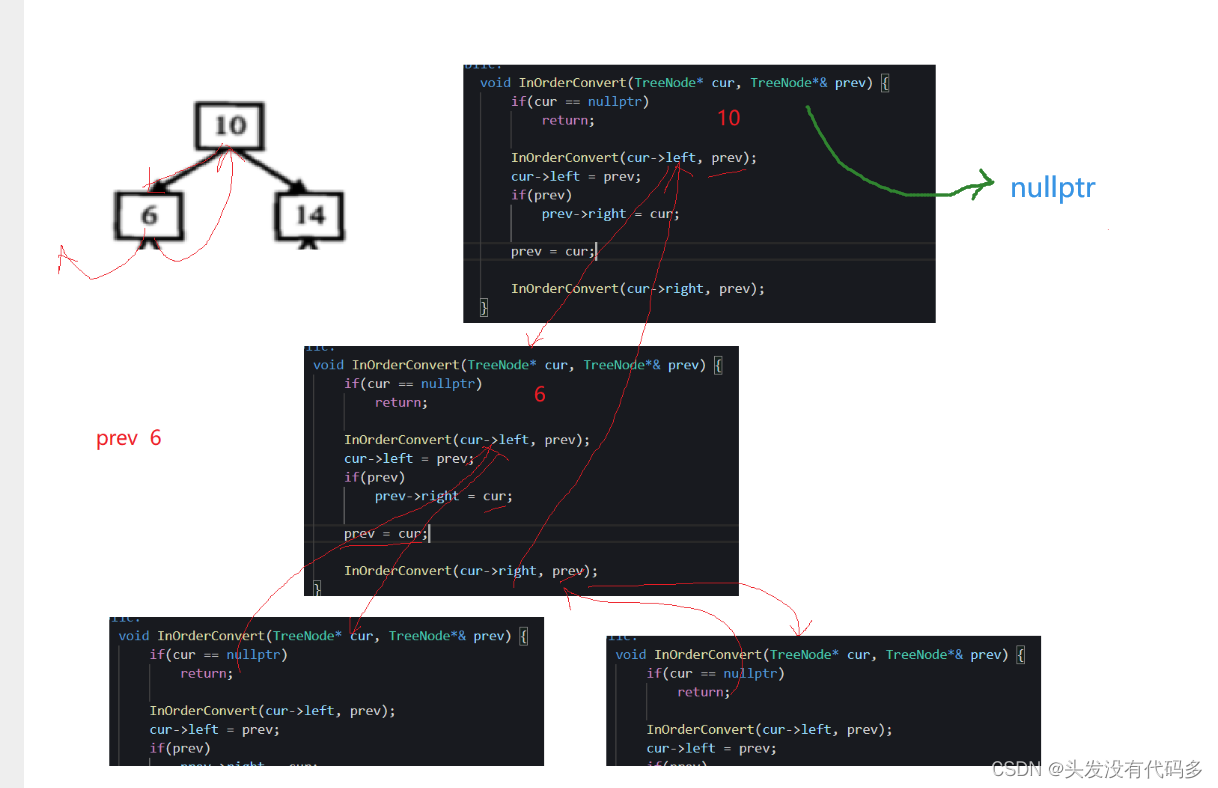
class Solution { public: void InOderConvert(TreeNode*cur,TreeNode*& prev) { if(cur==nullptr) return ; InOderConvert(cur->left,prev); cur->left=prev; if(prev) prev->right=cur; prev=cur; InOderConvert(cur->right,prev); } TreeNode* Convert(TreeNode* pRootOfTree) { TreeNode* prev=nullptr; InOderConvert(pRootOfTree,prev); TreeNode* head=pRootOfTree; while(head&&head->left) { head=head->left; } return head; } };最后要返回链表头部,根据根节点往左边找即可找到头部,prev要用引用,是因为递归返回上一层的时候要把确定新的prev的位置,不然prev在第一层是空,第二层是6,当第二成返回第一层时,cur->left=prev,此时应该是10->6,而这里不加引用就是10->nulllptr
6.从前序与中序遍历构建二叉树
105. 从前序与中序遍历序列构造二叉树 - 力扣(LeetCode)

大思路:前序创建树,中序分割左右子树
前序可以确定根
class Solution { public: TreeNode* _buildTree(vector<int>& preorder, vector<int>& inorder,int& prei,int inbegin,int inend) { if(inbegin>inend) return nullptr; TreeNode *root=new TreeNode(preorder[prei++]);//分割中序 int ini=inbegin; while(ini<=inend) { if(inorder[ini]==root->val) break; else ++ini; }//创建根 //[inbegin,ini-1]ini [ini,inend] root->left=_buildTree(preorder,inorder,prei,inbegin,ini-1); root->right=_buildTree(preorder,inorder,prei,ini+1,inend); return root; } TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) { int i=0; return _buildTree(preorder,inorder,i,0,inorder.size()-1); } };