决策树的基本构建流程
决策树的本质是挖掘有效的分类规则,然后以树的形式呈现。
这里有两个重点:
- 有效的分类规则;
- 树的形式。
有效的分类规则:叶子节点纯度越高越好,就像我们分红豆和黄豆一样,我们当然是想把红豆和黄豆完全分开。
这里标签的纯度的衡量指标有:
- 分类误差;
- 信息熵(Entropy);
- 基尼系数(Gini)。
我们举例来看看这三个指标是如何计算的:
对于单个数据集
假如我们有10条样本,6条0类样本,4条1类样本
则0类样本占:
6
10
\frac{6}{10}
106
1类样本占:
4
10
\frac{4}{10}
104
分类误差(1-多数类的占比):
1
−
6
10
=
0.4
1-\frac{6}{10}=0.4
1−106=0.4
信息熵:
−
6
10
∗
l
o
g
2
6
10
−
4
10
∗
l
o
g
2
4
10
=
0.97
-\frac{6}{10}*log_2\frac{6}{10}-\frac{4}{10}*log_2\frac{4}{10} =0.97
−106∗log2106−104∗log2104=0.97
基尼系数:
1
−
(
(
6
10
)
2
+
(
4
10
)
2
)
=
0.48
1-((\frac{6}{10})^2+(\frac{4}{10})^2)=0.48
1−((106)2+(104)2)=0.48
对于多个数据集
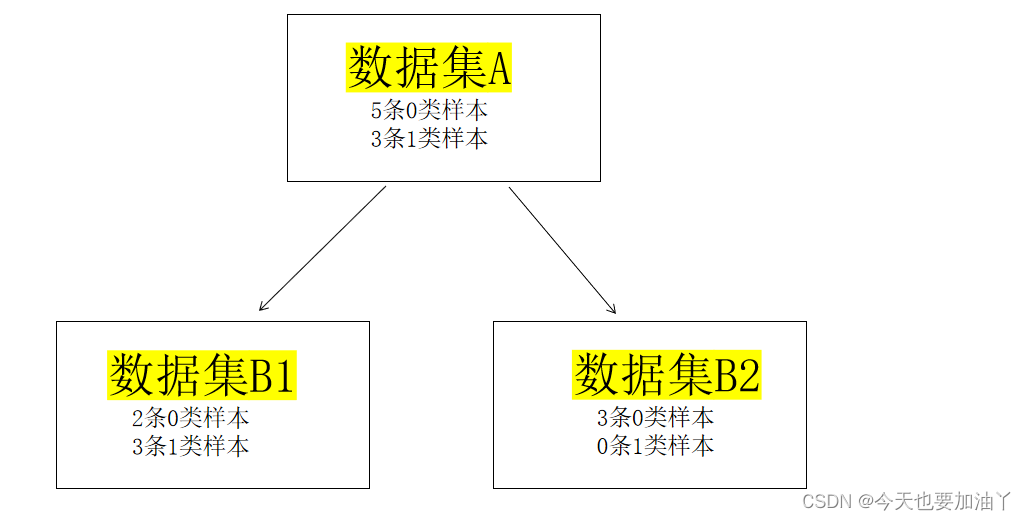
如何计算B1,B2两个子节点整体的评估指标?
这里以基尼系数为例
Gini_B1 = 1 − ( ( 2 5 ) 2 + ( 3 5 ) 2 ) = 0.48 1-((\frac{2}{5})^2+(\frac{3}{5})^2)=0.48 1−((52)2+(53)2)=0.48
Gini_B2 = 0
Gini_B = 5 8 \frac{5}{8} 85*Gini_B1 + 3 8 \frac{3}{8} 83*Gini_B2= 5 8 ∗ 0.48 \frac{5}{8}*0.48 85∗0.48+ 3 8 ∗ 0 \frac{3}{8}*0 83∗0=0.3
介绍完了有效的分类规则,我们再来看看第二个重点:树的形式。
下面简单画一下二层分类树。
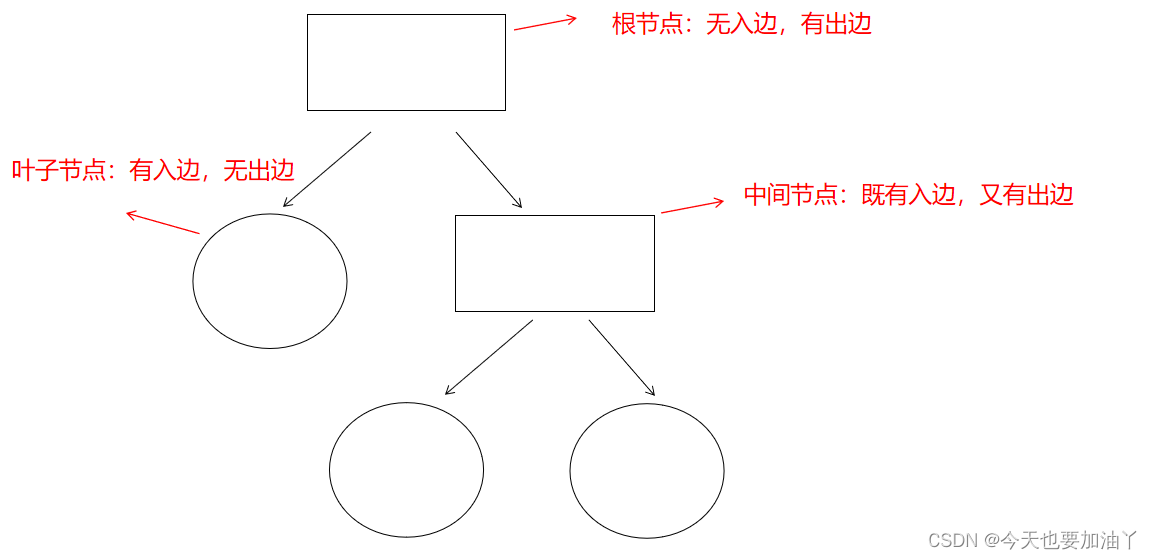
主流的决策树分类类别可划分为:
- D3(Iterative Dichotomiser 3) 、C4.5、C5.0决策树
- CART(Classification and Regression Trees)决策树
- CHAID(Chi-square automatic interaction detection)树
下面我们分别来看看决策树构建重点问题
1. 决策树的生长方向?
决策树生长的方向也就是令每个划分出来的子集纯度越来越高的方向
2. 如何挑选有效的分类规则?
选择信息增益最大的
假设我们有age列:

首先逐列对特征进行数值排序:

然后寻找特征不同取值之间的中间点为切点:

N个取值,有N-1种划分方式
这里有10个取值,所以有9种划分方式将数据集一分为二。
假设我们以10和9的中间点为划分方式
10
+
9
2
=
9.5
\frac{10+9}{2}=9.5
210+9=9.5
则我们可以以age是否小于等于9.5为划分规则,将数据集一分为二。
Notes:
1.CART(二叉树)用这种方法同时处理连续变量(预测值是划分后子数据集的均值)和离散变量;
2. C4.5连续变量用这种方式,离散变量用列的取值。
信息增益的计算:
CART Gain = Gini(父节点)- Gini(子节点)
ID3和C4.5 Gain = Entropy(父节点)- Entropy(子节点)
3. 如何停止迭代生长?
收敛条件:
(1)两轮迭代损失函数的差值小于某个值;
(2)限制最大迭代次数,也就是约束树最多生长几层





![[AutoSar]BSW_OS 06 Autosar OS_Alarms](https://img-blog.csdnimg.cn/direct/b8b0f588cd694a568eddcfe8e054c463.png)