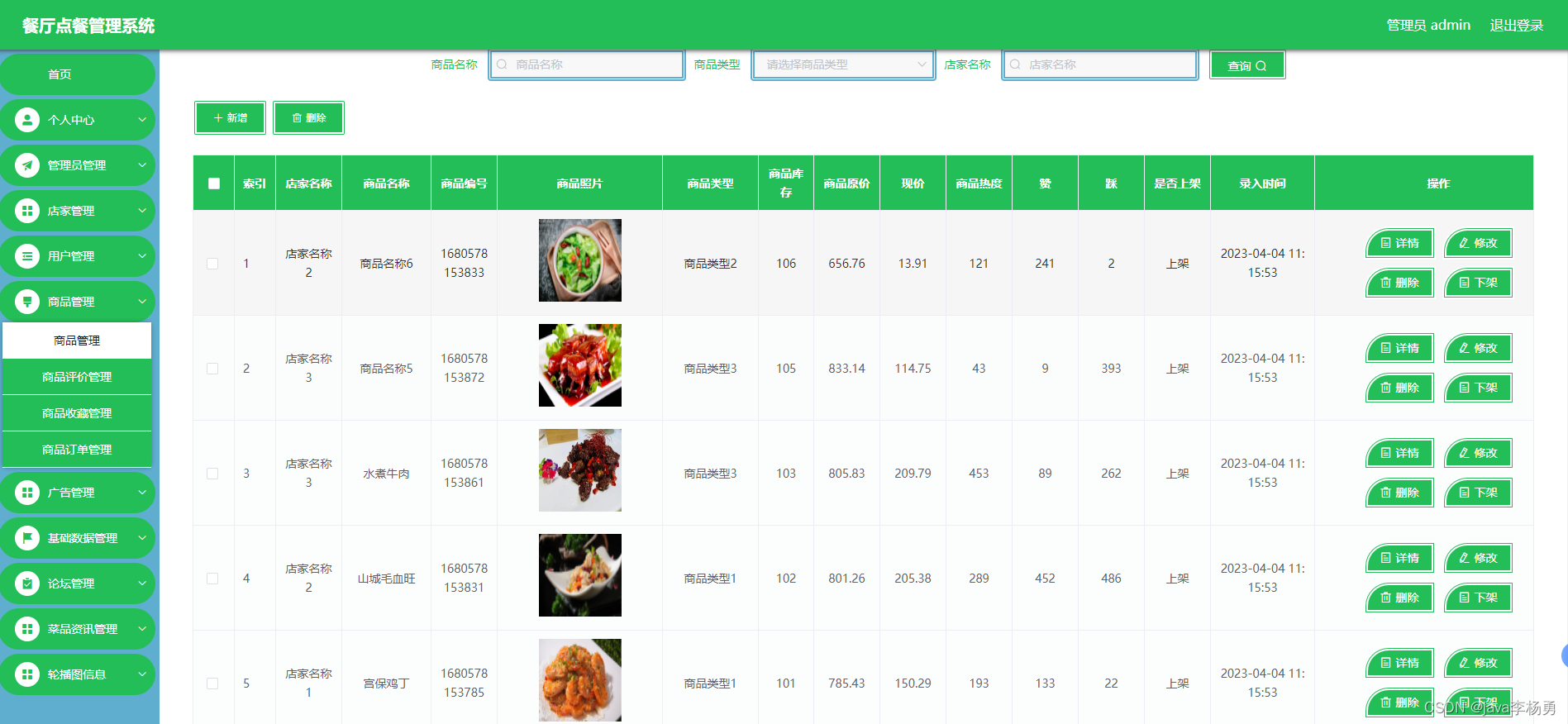
- 39. 组合总和

// 剪枝优化 class Solution { public List<List<Integer>> combinationSum(int[] candidates, int target) { List<List<Integer>> res = new ArrayList<>(); Arrays.sort(candidates); // 先进行排序 backtracking(res, new ArrayList<>(), candidates, target, 0, 0); return res; } public void backtracking(List<List<Integer>> res, List<Integer> path, int[] candidates, int target, int sum, int idx) { // 找到了数字和为 target 的组合 if (sum == target) { res.add(new ArrayList<>(path)); return; } for (int i = idx; i < candidates.length; i++) { // 如果 sum + candidates[i] > target 就终止遍历 if (sum + candidates[i] > target) break; path.add(candidates[i]); backtracking(res, path, candidates, target, sum + candidates[i], i); path.remove(path.size() - 1); // 回溯,移除路径 path 最后一个元素 } } }思路:典型的回溯算法,套用回溯三部曲就可以,这道题可以在for循环里面做剪枝操作,if(sum + candidates[i])>target 就终止遍历
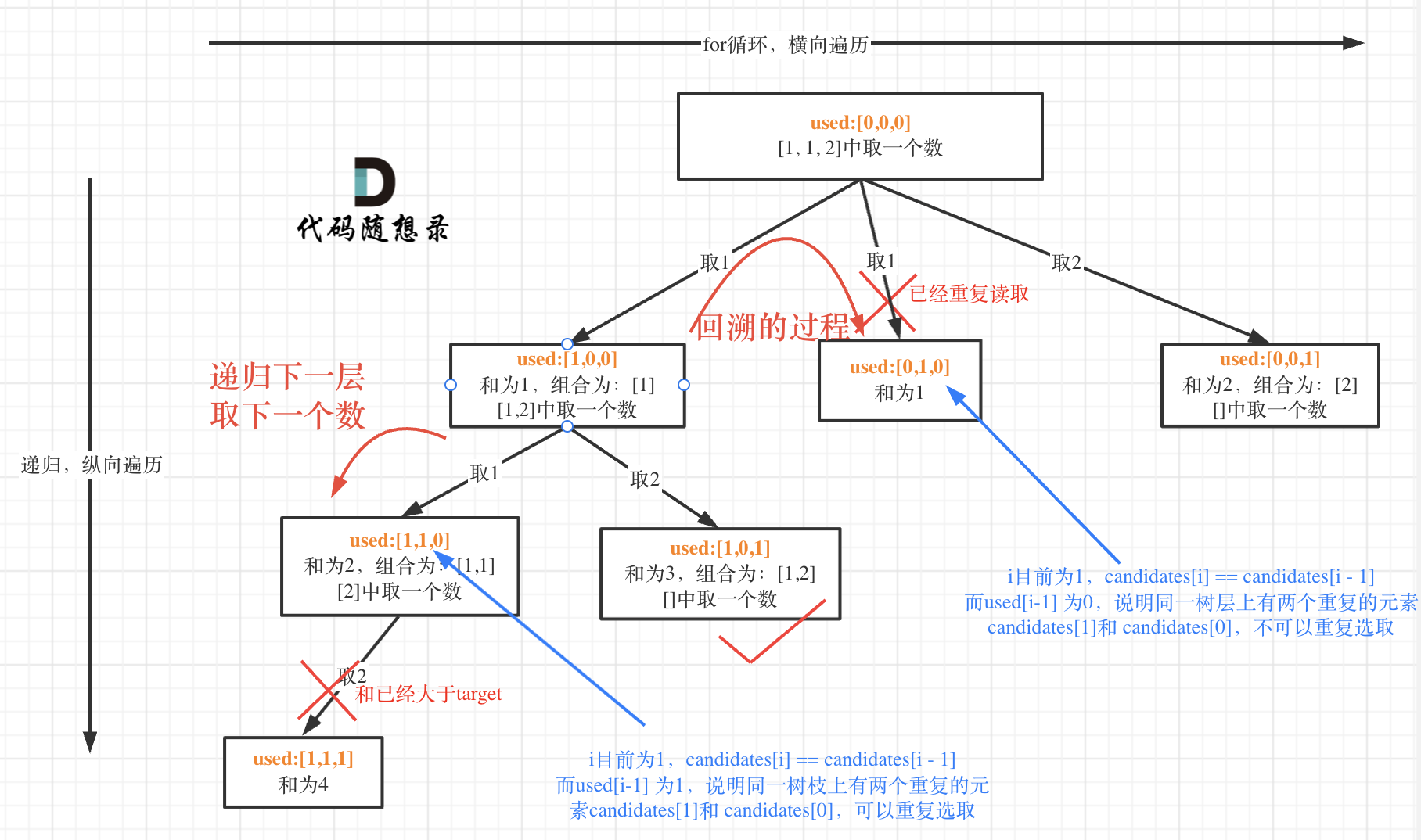
- 40.组合总和II

class Solution { LinkedList<Integer> path = new LinkedList<>(); List<List<Integer>> ans = new ArrayList<>(); boolean[] used; int sum = 0; public List<List<Integer>> combinationSum2(int[] candidates, int target) { used = new boolean[candidates.length]; // 加标志数组,用来辅助判断同层节点是否已经遍历 Arrays.fill(used, false); // 为了将重复的数字都放到一起,所以先进行排序 Arrays.sort(candidates); backTracking(candidates, target, 0); return ans; } private void backTracking(int[] candidates, int target, int startIndex) { if (sum == target) { ans.add(new ArrayList(path)); } for (int i = startIndex; i < candidates.length; i++) { if (sum + candidates[i] > target) { break; } // 出现重复节点,同层的第一个节点已经被访问过,所以直接跳过 if (i > 0 && candidates[i] == candidates[i - 1] && !used[i - 1]) { continue; } used[i] = true; sum += candidates[i]; path.add(candidates[i]); // 每个节点仅能选择一次,所以从下一位开始 backTracking(candidates, target, i + 1); used[i] = false; sum -= candidates[i]; path.removeLast(); } } }思路:回溯思路与上题差不多,主要是去重的操作,去重分为树枝去重和树层去重,本题是树层去重,同一层的数据,与前一个数据相等时,去重(跳过),用used[i-1]==false保证是同一层的而不是同一个树枝。
-
- 131.分割回文串

class Solution { List<List<String>>result = new ArrayList<>(); LinkedList<String>path = new LinkedList<>(); public List<List<String>> partition(String s) { backTracking(s, 0); return result; } public void backTracking(String s, int startIndex){ if(startIndex == s.length()){ result.add(new ArrayList<>(path)); } for(int i = startIndex ; i < s.length() ; i++){ if(isPalindrome(s, startIndex, i) == true){ path.add(s.substring(startIndex, i+1)); }else{ continue; } backTracking(s, i+1); path.removeLast(); } } public boolean isPalindrome(String s, int startIndex, int endIndex){ for(int i = startIndex, j = endIndex ; i < j ; i++, j--){ if(s.charAt(i) != s.charAt(j)){ return false; } } return true; } }思路:该题和组合问题类似,主要是要理清startIndex代表分割位置的思想,相当于画线操作,当一个区间为回文串的时候,add进path中,回溯终点是startIndex==s.length()
代码随想录算法训练营29期|day27 任务以及具体安排
news2026/2/16 3:13:05
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/1404610.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
ARM_Linux中GCC编译器的使用
目录 前言:
GCC编译过程:
预处理:
编译阶段:
汇编:
链接阶段
GCC的常见使用 前言:
什么是GCC: gcc的全称是GNU Compiler Collection,它是一个能够编译多种语言的编译器。最开始gcc是作为C语言的编译器(GNU C Co…
linux之安装配置VM+CentOS7+换源
文章目录 一、centos07安装二、CentOS 07网络配置2.1解决CentOS 07网络名不出现问题此博主的论文可以解决2.2配置(命令: 【ip a】也可查看ip地址) 三、使用链接工具链接CentOS进行命令控制四、换软件源 一、centos07安装
1、在vmvare中新建虚拟机 2、下…
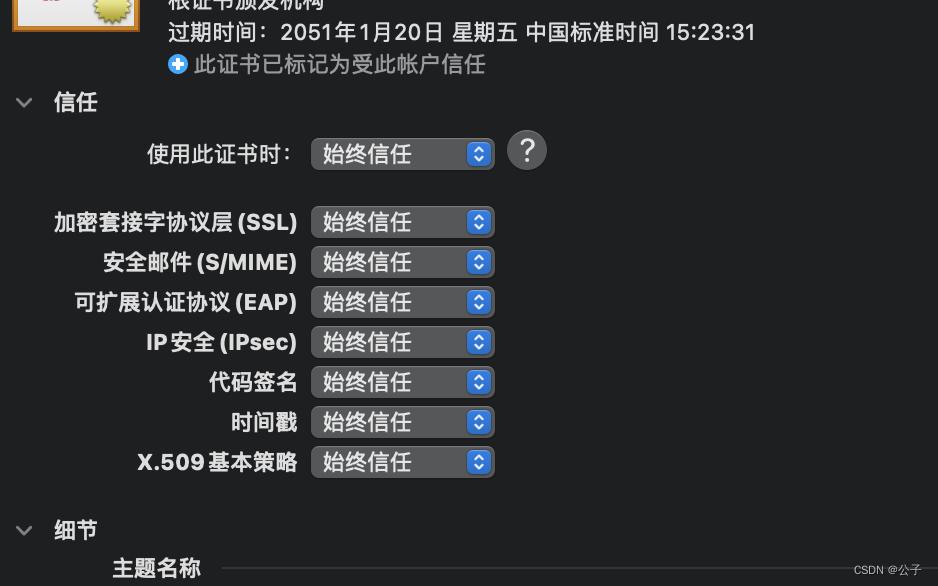
charles mac抓包unknown问题
第一步:mac上安装Charles后,mac安装证书: 第二步:mac上信任证书 第三步:手机上安装证书 安装提示:电脑上通过help–>SSLProxying–> Install Charles Root Ceriticate on a Mobile Device or Remote …
微信小程序从入门到进阶(二)
数据请求
wx.request发起网络请求,请求的方式主要分为两种: get 请求 post 请求
// get请求
// html
<view><button type"primary" bindtap"onGetClick">发起 get 请求</button>
</view>
// js
// inde…
redis 入门及相关知识汇总
什么是 Redis ? 1,相对于mysql ,oracle , 这种关系西数据库, 我们还有非关系数据库服务,他的产生是为了,解决常规数据库的并发能力,传统的关系型数据库受限于IO 和性能瓶颈ÿ…
xshell可以远程登录服务器但是vscode一直显示让输入密码的解决方案
vscode报错 但是xshell可以登录
原因:可能因为我上一次没有恰当的退出远程链接导致的,我每次退出远程都是直接强制关闭VScode。
解决方法:打开VScode的 view (查看) palette(命令面板)然后输…
[AutoSar]BSW_OS 06 Autosar OS_Alarms
一、 目录 一、关键词平台说明一、Timer1.1 配置1.2Periodical Interrupt Timer (PIT)和High Resolution Timer (HRT) 二、Alarm 工作机制三、Code3.1创建一个15ms的runnable3.2mapping到basic task3.3生成代码 关键词
嵌入式、C语言、autosar、OS、BSW
平台说明
项目ValueO…
还在用JS?过来看看GS
什么是GS?GS是我自创的一门编程语言,全名叫“GreatScript”,是一门类型化语言,可以编译成JavaScript。简单来说,就是又一门TypeScript。
GreatScript的生态位跟Typescript,CoffeeScript,ReScri…
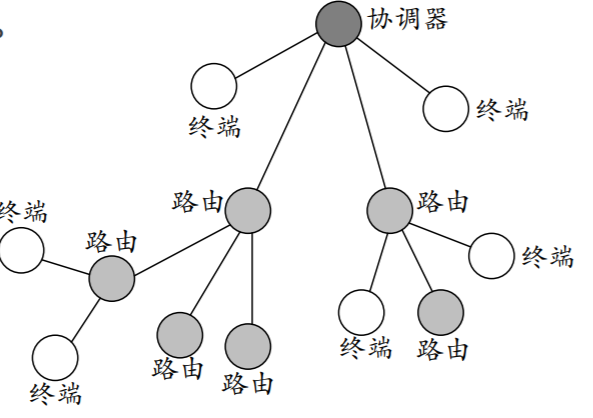
ZigBee学习(一)
文章目录 一、ZigBee介绍二、IEEE 802.15.42.1 物理层2.2 MAC层2.3 如何实现网络和设备寻址2.4 能量管理 三、ZigBee网络拓扑结构四、ZigBee配置参数 一、ZigBee介绍 ZigBee是一种基于IEEE 802.15.4标准的高级通信协议,它被设计用于低速率、低功耗和短距离无线通信&…
带头 + 双向 + 循环链表增删查改实现
目录
源码:
List.c文件:
List.h文件:
简单的测试: 很简单,没什么好说的,直接上源码。 源码:
List.c文件:
#include"DLList.h"ListNode* creadNode(LTDataType x)
{L…
自己重装Win10系统详细步骤教程
用户不喜欢自己电脑当前的操作系统,想自己重新一款喜欢的Win10系统,但不知道如何操作才能重新安装系统Win10?以下小编带来自己重装Win10系统详细步骤教程,帮助用户们轻轻松松地完成Win10系统的重装,快速体验Win10系统的…
2023.1.21 关于 Redis 主从复制详解
目录
引言
单点问题
分布式系统
主从模式
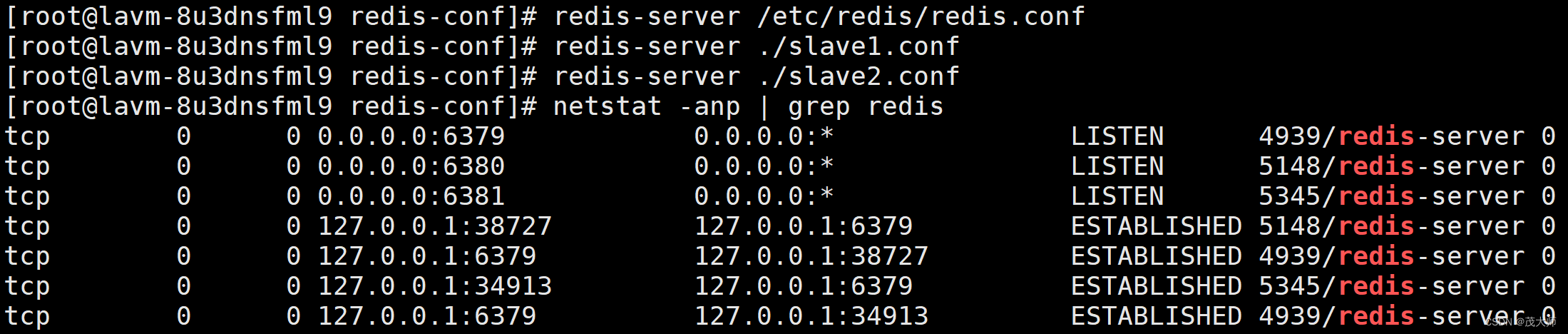
配置 Redis 主从结构
断开主从关系
切换主从关系
补充知识点一
只读
网络延迟 拓扑结构
一主一从
一主多从
树形主从结构
主从复制的基本流程
数据同步
replicationid
offset
pzync 运行流程
具体流程 补充知识点二…
JS 将字符串‘10.3%‘ 经过运算加2转换为 ‘12.3%‘
文章目录 需求分析 需求
已知 字符串 a ‘10.3%’,现需将转换为 字符串’12.3%’
分析
去掉百分号,将字符串转换为数字
const aNumber parseFloat(10.3%);
const resultNumber aNumber 2;将结果转换为带百分号的字符串
const resultString re…
〖大前端 - ES6篇①〗- ES6简介
说明:该文属于 大前端全栈架构白宝书专栏,目前阶段免费,如需要项目实战或者是体系化资源,文末名片加V!作者:哈哥撩编程,十余年工作经验, 从事过全栈研发、产品经理等工作,目前在公司…
2024年Java SpringBoot 计算机软件毕业设计题目推荐
博主介绍:✌全网粉丝30W,csdn特邀作者、博客专家、CSDN新星计划导师、Java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和学生毕业项目实战,高校老师/讲师/同行交流合作✌ 主要内容:SpringBoot、Vue、SSM、HLM…
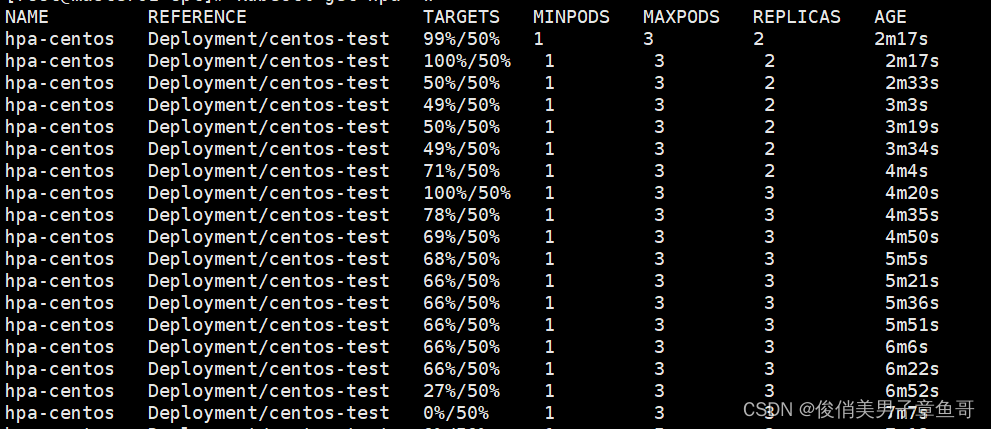
k8s---pod的水平自动伸缩HPA
HPA:Horizontal Pod Autoscaling是pod的水平自动伸缩。是k8s自带的模块
pod占用CPU的比率到达一定的阈值会触发伸缩机制。
replication controller:副本控制器。控制pod的副本数
deployment controller:节点控制器。部署pod
hpa控制副本的…
浅析位运算符(左移、右移、与、或、异或)
C语言是一种很奇妙的语言,它既有高级语言的特点,又有低级语言的特点,支持位运算让它更方便于硬件编程。
一、左移运算符(<<) 左移运算就是将一个二进制位的操作数按指定位数整体向左移位,移出位被丢…
【力扣】记录一下竞赛分上 Knight
记录一下力扣上 Knight
力扣的题还是相对来说比较简单的,前两个月写的题多一点,后面几乎都是只做了每日一题,感觉正常来说刷个两三个月的题水平就差不多够了,甚至在我才刷半个月的时候就可以做三题了,排名和现在差不多…
手机上菜谱记录簿在哪 用备忘录放大看菜谱更清晰
作为一个热爱生活的现代人,我深知健康饮食的重要性。然而,每当我想亲手为自己和家人烹饪美食时,厨艺的不精常常让我望而却步。好在互联网时代,网上搜罗的各式菜谱成了我的救星。但问题是,每次做菜时都得反复查找&#…
docker运行redis,jdk,nginx
Redis
1.查询redis
[rootlocalhost ~]# docker search redis
NAME DESCRIPTION STARS OFFICIAL
redis Redis is an open source key-value store that… 12620 …



![[AutoSar]BSW_OS 06 Autosar OS_Alarms](https://img-blog.csdnimg.cn/direct/b8b0f588cd694a568eddcfe8e054c463.png)