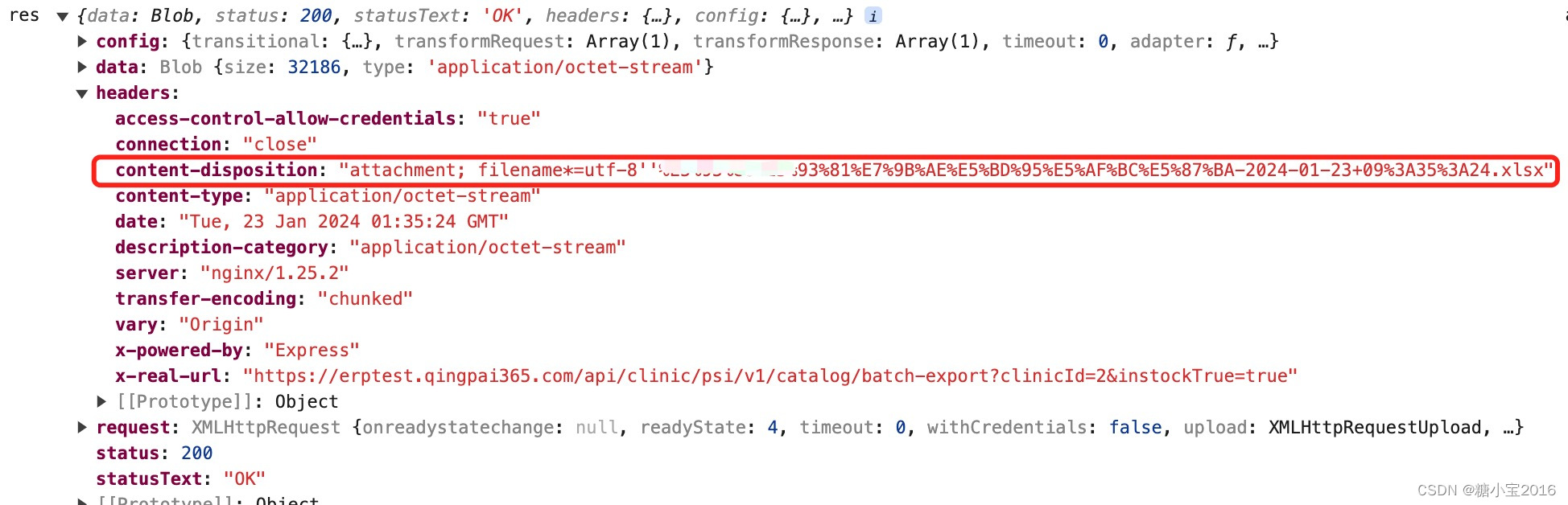
题目地址：

101. 对称二叉树 - 力扣（LeetCode）

难度：简单

今天刷对称二叉树，大家有兴趣可以点上面链接，看看题目要求，试着做一下。

题目：

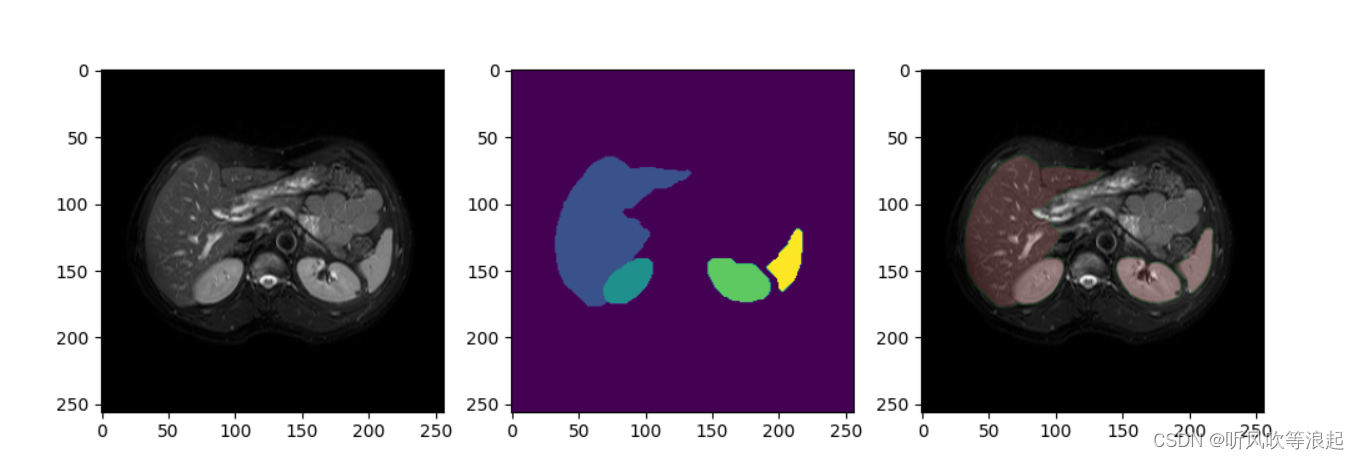
给你一个二叉树的根节点 root ， 检查它是否轴对称。

我们直接看题解吧：

快速理解解题思路小建议：

可以先简单看一下解题思路，然后照着代码看思路，会更容易理解一些

解题方法：

方法1，递归

方法2，迭代

解题分析：

对称二叉树定义： 对于树中 任意两个对称节点 L 和 R ，一定有：

    ·L.val = R.val ：即此两对称节点值相等。

    ·L.left.val = R.right.val ：即 L的 左子节点 和 R的右子节点 对称。

    ·L.right.val = R.left.val ：即 L的 右子节点 和 R的左子节点对称。

根据以上规律，考虑从顶至底递归，判断每对左右节点是否对称，从而判断树是否为对称二叉树。

解题思路（递归）：

主要设计一个递归函数，通过‘同步移动’两个指针的方法遍历树，利用两个指针从根节点开始向左右子树移动，每次检查当前节点的值是否相等，若相等再判断左右子树是否对称。

算法流程：

1、在函数 isSymmetric(root) ：

    特例处理： 若根节点 root 为空，则直接返回 true。

    返回值： 即 check(root.left, root.right) ;

2、函数check(L, R)：

    终止条件：

         ·当 L 和 R 同时越过叶节点： 此树从顶至底的节点都对称，因此返回 true 。

         ·当 L或R中只有一个越过叶节点： 此树不对称，因此返回 false。

        · 当节点 L 值 ≠ 节点 R 值：此树不对称，因此返回 false。

3、递推工作：

     判断两节点 L.left 和 R.right 是否对称,即 check(L.left, R.right) 。

     判断两节点 L.right 和 R.left 是否对称，即 check(L.right, R.left) 。

    返回值： 两对节点都对称时，才是对称树，因此用与逻辑符 && 连接。

代码实现：

class Solution {
    public boolean isSymmetric(TreeNode root) {
        return check(root, root);
    }

    public boolean check(TreeNode L, TreeNode R) {
        if ( L == null && R== null) {
            return true;
        }
        if ( L == null || R== null|| L.val == R.val) {
            return false;
        }
        return check( L.left, R.right) && check( L.right,R.left);
    }
}

解题思路（迭代）：

  首先引入一个队列（递归改迭代的常用方法）。

初始化时，将根节点入队两次，每次提取节点比较节点值(队列每两个连续节点应相等，且其子树互为镜像)

接着将两节点的左右子节点以相反顺序插入队列中。

最后当队列为空，或树不为空时结束

代码实现：

class Solution {
public:
    bool check(TreeNode *u, TreeNode *v) {
        queue <TreeNode*> q;  //创建队列
        q.push(u); q.push(v);  //节点入队
        while (!q.empty()) {
            u = q.front(); q.pop();
            v = q.front(); q.pop();
            if (!u && !v) continue;
            if ((!u || !v) || (u->val != v->val)) return false;

            q.push(u->left); 
            q.push(v->right);

            q.push(u->right); 
            q.push(v->left);
        }
        return true;
    }

    bool isSymmetric(TreeNode* root) {
        return check(root, root);  //调用check方法
    }
};