DDOD（Disentangle Your Dense Object Detector）解析

paper：Disentangle Your Dense Object Detector

official implementation：https://github.com/zehuichen123/DDOD

third-party implementation：https://github.com/open-mmlab/mmdetection/tree/main/configs/ddod

存在的问题

现有的目标检测模型的设计中存在许多联结conjunctions，本文研究了三种conjunction：1）只有在分类head中分配为positive的样本才被用来训练回归head。2）在当前分类和回归两个平行分支的设计中，两个head共享相同的输入特征。3）在计算损失时，对分布在不同FPN level的样本进行同等的对待。作者首先进行了一系列实验证明解耦这些联结可以持续提升性能。基于这些方法，作者提出了Disentangled Dense Object Detector（DDOD），其中设计了简单有效的解耦机制并且集成到了目前SOTA的密集目标检测模型中。

本文的创新点

本文通过实验证明了解耦上述三种联结可以显著提升模型性能。对于标签分配的联结，针对分类和回归设计了分离的label assigner，从而可以分别为两个分支挑选出最合适的训练集。对于空间特征的联结，基于可变形卷积提出了一种自适应特征解耦模块（adaptive feature disentanglement module），可以自动关注有利于分类和回归的不同特征。对于FPN监督的联结，设计了一种重加权机制，基于每一层的正样本，自适应的调整不同FPN层的监督大小。结合上述三点，提出了一种新的dense detector，DDOD(Disentangled Dense Object Detector)。

预实验

作者首先做了一些预实验来验证三种联结对模型的负作用。

Label Assignment Conjunction

回归损失只应用于分类分支中的“前景”样本这种conjunction是出于历史原因。只有与GT box的IoU大于设定阈值的样本才视为正样本，但是这个阈值不需要与分类的阈值一致，并且在推理时不存在“正样本”的概念因为每个anchor box或center point都会被用于预测的回归器。因此为边界框的回归单独设置一个阈值时合理的。为了验证这个假设，作者用不同的分类和回归IoU阈值训练了RetinaNet，结果如表1所示。可以看出，当分类头的IoU为0.5回归的IoU为0.4时性能最好。因此在DDOD中，通过在分类和回归分支上采用不同的label assigner来解耦assignment conjunction。

Spatial Feature Conjunction

像RetinaNet这种分类和回归是两个平行且结构相同的设计，意味着它们在特征图中对应的感受区域也是相同的。但如TSD中提到的，分类和回归任务关注的区域是不同的：语义信息丰富的区域有助于分类而轮廓区域对于回归是至关重要的。作者使用GradCAM对于分类和回归的sensitive region进行了可视化，如图2所示，可以看出两个任务关注的区域确实是不同的。

Supervision Conjunction in FPN

目前基于FPN的密集检测模型的常用实现是将不同层的输出“flatten and concatenated”然后计算损失，这使得不同层的监督变得联结。但因为不同层的样本分布明显不平衡，随着特征分辨率的增加，特征的大小也以二次指数的形式增加，这使得训练被低层的样本dominate，高层的样本缺乏监督，从而影响大目标的检测。一个克服这个问题的简单想法是给高层样本赋予更大的权重来弥补监督的缺失，作者采用了不同的重加权策略进行了实验，结果如表2所示，其中只设置了最低层和最高处的权重，其余层的权重用插值计算得到。可以看到，最好的策略是从1线性增加到2，最坏的策略是从3到1线性递减。

方法介绍

DDOD的完整结构如图3所示

Label Assignment Disentanglement

基于上述实验结果，本文对分类和回归分支分别设计了不同的标签分配策略。对于输入图片 \(I\)，假设有 \(N\) 个GT，基于预设anchor有 \(P\) 个预测，对于每个候选（anchor或center point）\(P_{i}\)，输出每个类别的前景概率 \(\hat{p}(i)\) 和回归的bounding box \(\hat{b}(i)\)。基于此，cost matrix如下

其中 \(C_{i,\pi(i)}\in[0,1]\) 表示第 \(\pi(i)\) 个预测的匹配质量，\(\Omega_{i}\) 表示第 \(i\) 个GT的候选预测。为了稳定训练过程加速收敛，只有中心点落入GT box的候选才被认为是可能的前景。标签分配时，从FPN每层选择cost value最大的K个预测。如果候选对象的匹配质量超过了用ATSS等batch statistics计算得到的自适应阈值时，将其分配为前景样本。、

为了解耦分类和回归的标签分配，本文还引入了一个超参 \(\alpha\) 来平衡两者的贡献，然后通过消融实验确定了 \(\alpha\) 的最佳值。

Spatial Feature Disentanglement

借助可变形卷积，模型可以关注到特征图中不同的空间区域，作者提出了自适应特征解耦模块，其中在每个位置 \(p_{n}\) 预测一个可学习的卷积偏移，从而针对当前任务学习自适应的挑选空间特征。对于特征图 \(F\) 上的位置 \(p_{i}\) 有

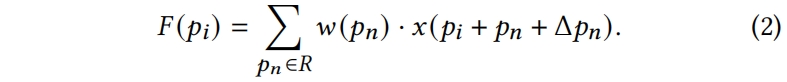
关于可变形卷积的具体介绍见https://blog.csdn.net/ooooocj/article/details/128539972

Pyramid Supervision Disentanglement

对于FPN conjunction，本文提出了FPN分层损失。不平衡的根本原因在于每层样本的不平衡，因此本文直接用每层的样本数量作为指标来确定该层监督的权重应该增加还是降低。\(L_{i}\) 层上关于损失 \(L\) 的重加权系数 \(w\) 根据下式得到

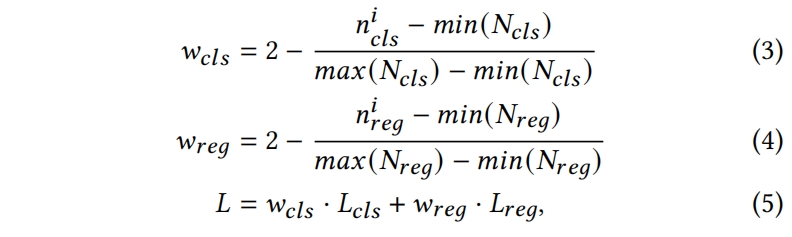
其中 \(n_{cls}^{i}\) 和 \(n_{reg}^{i}\) 分别是第 \(i\) 层FPN上的正负样本数量，\(N_{cls}\) 和 \(N_{reg}\) 分别是所有层 \(n_{cls}^{i}\) 和 \(n_{reg}^{i}\) 的集和。此外作者还采用了moving average的方式来缓解不同图片上样本的分布差异。具体来说，每个interation \(J\)，采用每个FPN层 \(i\) 上正样本的累积数量 \( {\textstyle \sum_{j=0}^{J}} n^{i}_{cls/reg}\) 来计算 \(w\)。

代码解析

这里以mmdetection中的实现为例，其中具体实现在mmdet/models/dense_heads/ddod_head.py中。

首先是label assignment的解耦，从配置文件中可以看出分类和回归分别采用了ATSSAssigner，并且alpha值不同。

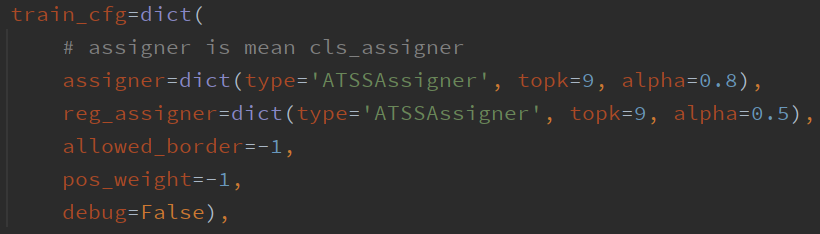
在具体实现atss_assigner.py中，具体实现如下。这里变量alpha只在DDOD中不为None，其它情况就是原始的ATSS。最后一行overlaps的实现对应论文中的式(1)，alpha值越小，对应项overlaps**self.alpha越大，表示cost matirx更关注回归的质量，反之亦然。

# compute iou between all bbox and gt
if self.alpha is None:
    # ATSSAssigner
    overlaps = self.iou_calculator(priors, gt_bboxes)
    if ('scores' in pred_instances or 'bboxes' in pred_instances):
        warnings.warn(message)

else:
    # Dynamic cost ATSSAssigner in DDOD
    assert ('scores' in pred_instances
            and 'bboxes' in pred_instances), message
    cls_scores = pred_instances.scores
    bbox_preds = pred_instances.bboxes

    # compute cls cost for bbox and GT
    cls_cost = torch.sigmoid(cls_scores[:, gt_labels])

    # compute iou between all bbox and gt
    overlaps = self.iou_calculator(bbox_preds, gt_bboxes)

    # make sure that we are in element-wise multiplication
    assert cls_cost.shape == overlaps.shape

    # overlaps is actually a cost matrix
    overlaps = cls_cost**(1 - self.alpha) * overlaps**self.alpha

然后是两个检测头spatial feature的解耦，具体实现就是每个分支的第一个卷积改成了可变形卷积，具体实现如下

def _init_layers(self) -> None:
    """Initialize layers of the head."""
    self.relu = nn.ReLU(inplace=True)
    self.cls_convs = nn.ModuleList()
    self.reg_convs = nn.ModuleList()
    for i in range(self.stacked_convs):
        chn = self.in_channels if i == 0 else self.feat_channels
        self.cls_convs.append(
            ConvModule(
                chn,
                self.feat_channels,
                3,
                stride=1,
                padding=1,
                conv_cfg=dict(type='DCN', deform_groups=1)
                if i == 0 and self.use_dcn else self.conv_cfg,
                norm_cfg=self.norm_cfg))
        self.reg_convs.append(
            ConvModule(
                chn,
                self.feat_channels,
                3,
                stride=1,
                padding=1,
                conv_cfg=dict(type='DCN', deform_groups=1)
                if i == 0 and self.use_dcn else self.conv_cfg,
                norm_cfg=self.norm_cfg))

最后是FPN监督的解耦，具体实现如下

def calc_reweight_factor(self, labels_list: List[Tensor]) -> List[float]:
    """Compute reweight_factor for regression and classification loss."""
    # get pos samples for each level
    bg_class_ind = self.num_classes
    for ii, each_level_label in enumerate(labels_list):
        pos_inds = ((each_level_label >= 0) &
                    (each_level_label < bg_class_ind)).nonzero(
                        as_tuple=False).squeeze(1)
        self.cls_num_pos_samples_per_level[ii] += len(pos_inds)
    # get reweight factor from 1 ~ 2 with bilinear interpolation
    min_pos_samples = min(self.cls_num_pos_samples_per_level)
    max_pos_samples = max(self.cls_num_pos_samples_per_level)
    interval = 1. / (max_pos_samples - min_pos_samples + 1e-10)
    reweight_factor_per_level = []
    for pos_samples in self.cls_num_pos_samples_per_level:
        factor = 2. - (pos_samples - min_pos_samples) * interval
        reweight_factor_per_level.append(factor)
    return reweight_factor_per_level