坚持刷题｜二叉树的最大深度

news2024/11/16 7:50:38

文章目录

题目
考察点
代码实现
实现总结
扩展
- 用迭代的方式实现二叉树最大深度
- 可能的扩展问题

坚持刷题，老年痴呆追不上我，今天刷：二叉树的最大深度

题目

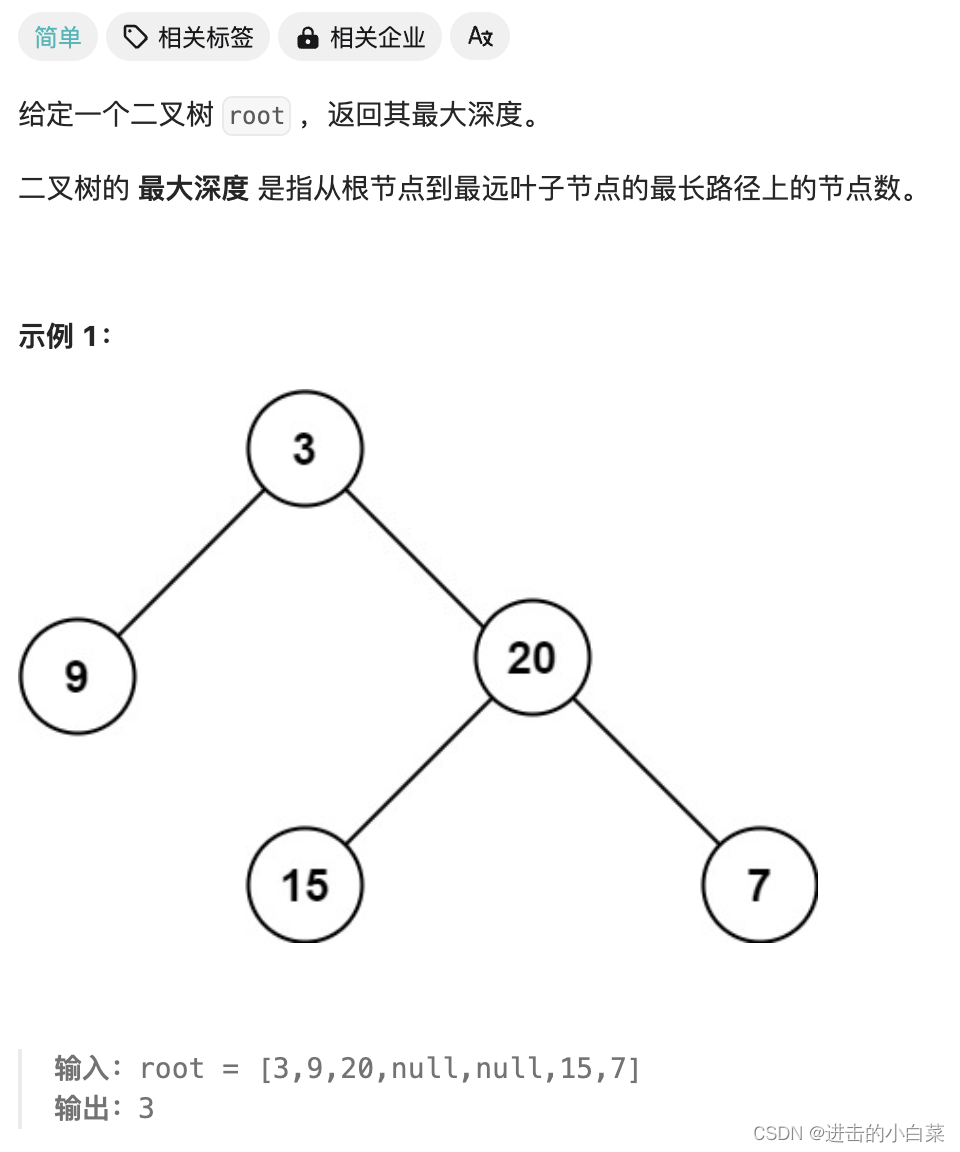
104.二叉树的最大深度
在这里插入图片描述

考察点

二叉树的基本实现：能够定义二叉树节点（TreeNode）以及构建一个二叉树的基本结构
递归的理解和运用：能够使用递归的方式遍历二叉树节点
树的深度计算：能够理解并实现计算二叉树深度的算法

代码实现

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    public TreeNode(int val) {
        this.val = val;
    }
}

public class BinaryTreeDepth {
    public int maxDepth(TreeNode root) {
        if (root == null) {
            return 0;
        } else {
            int leftDepth = maxDepth(root.left);
            int rightDepth = maxDepth(root.right);

            // 返回左右子树深度的较大值加上当前节点的深度（1）
            return Math.max(leftDepth, rightDepth) + 1;
        }
    }

    public static void main(String[] args) {
        // 创建一个二叉树示例
        TreeNode root = new TreeNode(1);
        root.left = new TreeNode(2);
        root.right = new TreeNode(3);
        root.left.left = new TreeNode(4);
        root.left.right = new TreeNode(5);

        BinaryTreeDepth binaryTreeDepth = new BinaryTreeDepth();
        int depth = binaryTreeDepth.maxDepth(root);

        System.out.println("二叉树的深度为：" + depth);
    }
}

实现总结

递归的理解和使用：通过递归计算左右子树的深度，并在递归的基础上计算当前节点的深度
树的深度计算：通过比较左右子树的深度，选择较大值，并在此基础上加上当前节点的深度（1），得到整个二叉树的深度
时间复杂度： O(N)，其中 N 是二叉树中的节点数。每个节点都会被访问一次，因此时间复杂度是线性的
空间复杂度： O(H)，其中 H 是二叉树的高度。递归调用会使用系统调用栈，因此空间复杂度取决于递归的深度，即树的高度。在最坏的情况下，如果树是一个单链表形式的完全不平衡树，空间复杂度为 O(N)；在最好的情况下，如果树是平衡二叉树，空间复杂度为 O(log N)
递归调用会占用栈空间，每次递归调用都会将当前状态保存在栈中，因此空间复杂度主要取决于递归的深度。在实际应用中，需要考虑递归深度是否可能达到系统栈的限制

扩展

用迭代的方式实现二叉树最大深度

import java.util.LinkedList;
import java.util.Queue;

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    public TreeNode(int val) {
        this.val = val;
    }
}

public class BinaryTreeDepth {
    public int maxDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }

        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        int depth = 0;

        while (!queue.isEmpty()) {
            int levelSize = queue.size();

            for (int i = 0; i < levelSize; i++) {
                TreeNode current = queue.poll();

                if (current.left != null) {
                    queue.offer(current.left);
                }

                if (current.right != null) {
                    queue.offer(current.right);
                }
            }

            depth++;
        }

        return depth;
    }

    public static void main(String[] args) {
        // 创建一个二叉树示例
        TreeNode root = new TreeNode(1);
        root.left = new TreeNode(2);
        root.right = new TreeNode(3);
        root.left.left = new TreeNode(4);
        root.left.right = new TreeNode(5);

        BinaryTreeDepth binaryTreeDepth = new BinaryTreeDepth();
        int depth = binaryTreeDepth.maxDepth(root);

        System.out.println("二叉树的深度为：" + depth);
    }
}