二分查找引入大O表示法

仅知道算法需要多长时间运行完毕还不够，还需要知道运行时间如何随列表长度增加而增加，这正是大O表示法的用武之地。

大O表示法

1. 大O表示法指出了算法有多块，之所以称作大O，单纯因为前面有个O(funny!)
2. 大O表示法指出了最糟糕情况下的运行时间
   

画格子

方法1：
一个个画出来，画16个格子就需要操作16次，所以为O(n)
方法2：
对折4次，画16个格子就需要操作4次，每次对半(log16=4)，所以为O(logn)

常见的大O

1. O(logn)，也叫对数时间，如：二分查找
2. O(n)，也叫线性时间，如：简单查找
3. O(n*logn)，如：快排（速度较快的排序方法）
4. O(n**2)，如：选择排序（速度较慢的排序方法）
5. O(n!)，如：旅行商问题解决方案（非常慢的算法）

小结

1. 算法的速度并非指运行时间，而是操作数的增速
2. 讨论算法的速度指的是，随着输入的增加，运行时间将以什么速度增加。（类似于速度与加速度）

O(n!)旅行商问题

有一个旅行商，需要前往5个城市，同时确保旅程最短，5个城市就有120种排列方式（考虑顺序：A51A52A53A54A55=5!=120，见排列组合）


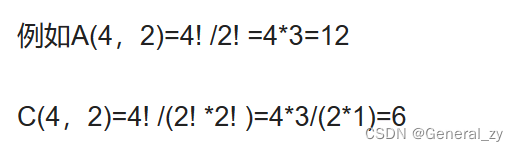
当城市为n时，就要进行n!次操作才能计算出结果，如果n过大，等你计算出来估计太阳了爆炸了。