基本思想

松弛问题无解，则整数规划无解

松弛问题的最优解是整数解，则他也是整数规划的最优解

如果松弛问题的解是非整数解，则对其增加割平面条件。

割平面条件：增加一个线性条件，通过不等式将可行区域割掉一部分，将部分的非整数解部分去掉，保留原问题整数的可行解，得到新的问题，重复过程。

结合案例说明使用时的具体步骤：

对松弛变量求解 

松弛问题的解是非整数解，需要对其增加割 平面 条件。

引入与解数目一样的松弛变量，将不等式变成等式。

 将等式分别消元得到两个都只有一个实解的等式

 松弛变量的系数化为整数部分和小数部分，

 将整数部分放一边，小数部分放在等式的另一边

 根据所有的x都是正整数得出不等式

 进而得出x3，x4的不等式

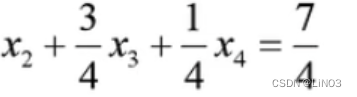
 再将其带回原来的等式，就可以得出附加的约束条件

x2<=1

再次计算线性规划得出整数解。

matlab上直接使用intlinprog求解器也可以直接得出整数答案

c=[-1,-1];
intcon=1:2;
A=[-1,1;3,1];
b=[1;4];
lb=[0,0];
[x,fval]=intlinprog(c,intcon,A,b,[],[],lb);
fval=-fval;

x=[1;1]

fval=2