---

引自同一作者百家号文章：「Python语言进阶」算法复杂度是什么？如何估算？

概念介绍

算法，可以理解为解决问题的方法和思路，不是一定得有代码的才叫算法，它是可以独立存在的，代码只是算法实现的一种载体。而我们评价算法的性能，也就是评价一个算法好不好，主要是评估算法的复杂度。

算法复杂度：分为（渐进）时间复杂度和（渐进）空间复杂度。这也是考量算法消耗计算机最重要的两种资源（时间、寄存器空间）的情况。时间复杂度：可以简单理解为电脑的基本运算的执行次数；空间复杂度：可以理解为电脑实现这个算法的过程中所开辟的存储空间大小。

算法分析一般指的复杂度分析，包括时间和空间两方面，其目的在于选择合适的算法和改进算法。那我们如何估算或表示算法的复杂度？答案是：大O法。

用$O(g(n))$来表示算法估算的渐进复杂度，$f(n)$表示实际复杂度，$g(n)$和$f(n)$成正比，$n$ 表示算法输入的数据规模。这里和前面都提到的“渐进”，指的是当输入数据规模趋近于无穷大的情况下算法的复杂度，它反映的是算法复杂度随着输入数据规模增加而提升的速度。

时间复杂度估算

刚才说，算法执行基本运算的次数用来描述时间复杂度，而现实中还会遇见说用执行时间来描述复杂度的，用执行时间来做性能分析的。而且Python有 timeit 库用来分析程序的系统运行时间，如下示例：

import time
from timeit import Timer


def func():
    s = 0
    for i in range(1000):
        s += i


# Timer(函数名_字符串，运行环境_字符串)
test = Timer('func()', 'from __main__ import func')
# timeit(1)，运行1次，参数省略则默认运行1000,000次
print(test.timeit(1))

在实际中，用执行时间来表示时间复杂度是很方便的，但因为执行时间的长短的影响因素很多，包括运行环境、算法随机性、算法和输入数据的适配性等，使得用不同条件下得到的执行时间来估算时间复杂度的做法不完全可靠。

而另一个对比的方式就是用 “大O法” 进行渐进复杂度的估算，通过估算超大规模下算法执行次数的增长速度，来评估算法效率，这种估计不受程序执行环境的影响。

先来看用 “大O法“ 计算时间复杂度的几条规则：

1. 用常数1等价替代不受数据规模影响的基本操作。如加法、赋值、打印等基本操作，它们在计算机中的执行时间是个极短的常数，而程序中的这部分与输入规模无关的操作，则可以统一为执行了1次；
2. 嵌套循环按乘法计算。如果有个两层循环，一层是循环 $n$ 次，另一层循环了 $m$ 次，且循环内的执行代码都只是基本操作，那这个循环操作的复杂度为 $n\times m$；在算法设计时尽量不要用太多层循环；
3. 分支操作按复杂度最大的分支进行计算，无特殊说明情况下，分支操作都是考虑最坏情况下的复杂度；
4. 只保留最高次项，并去除常数系数，前面说的$g(n)$与$f(n)$成正比就很好理解了，举个例子，$f(n)=2logn+100$，只保留最高次项，并去除常数系数，最后复杂度写为 $O(logn)$。

时间复杂度常见到的 $logn$ 是以 2 为底 $n$ 的对数

如下是时间复杂度为$O(1),O(logn),O(n)$的例子的代码：

# O(1)，不含循环
def o1(n):
    return n+n*3
    
# O(logn)，函数执行了logn次循环
def o_log_n(n):
    i = 1
    while i<n:
        i *= 2
    return i
    
# O(n)，函数循环了n次
def o_n(n):
    count = 0
    for i in range(n):
        count += i
    return count

那么问题来了：如果既有分支又有循环，那复杂度又要怎么估算呢？

对 $f(n)$ 来说很简单，把所有操作的复杂度加起来就行。但对于 $O()$ 来说，只保留其中主导的那一项。例如 $f(n)=nlogn+n$，则复杂度估算为 $O(nlogn)$。因为随着数据规模 $n$ 趋近于无穷，$nlogn$ 起到主导作用，另外一项 $+n$ 相对来说对复杂度的贡献不显著。当然，这里的默认前提是用同一个 $n$ 的时间复杂度。又例如，$f(n,m)=nlogn+n+m$，复杂度估算则为 $O(nlogn+m)$。

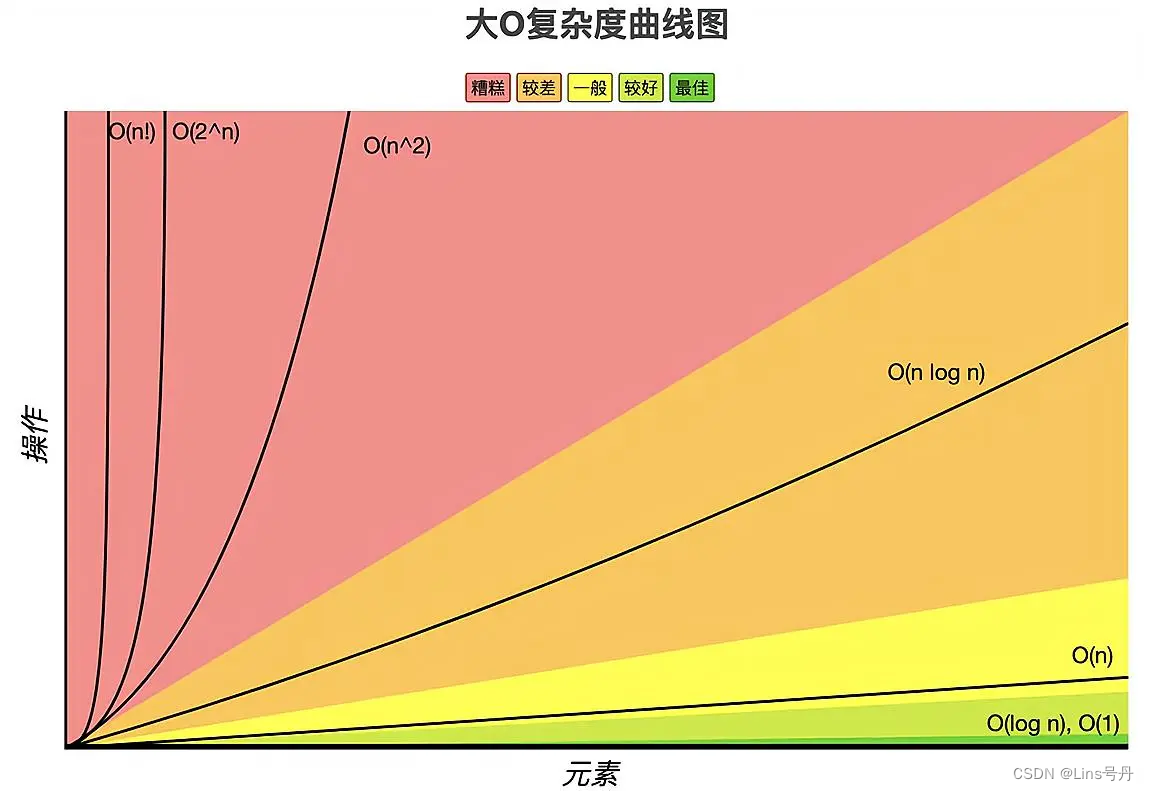
常见的大O时间复杂度曲线的高低排序如下，纵坐标表示操作的执行次数，横坐标表示输入数据的规模。

排序：$O(1)<O(logn)<O(n)<O(nlogn)<O(n^2)<O(2^n)<O(n!)$

空间复杂度估算

相比于时间复杂度，空间复杂度是很容易计算出来，其实就是算法在执行过程中，新开辟了多少用来存放变量值的存储空间，这个空间的大小即空间复杂度。同样的，存储一个值的空间看成是1（固定大小的空间），存储一个列表的空间为列表的长度，而变量的重新赋值不会改变空间复杂度。

空间复杂度的估算也是用 “大O法”，且遵循时间复杂度的估算规则，描述的是空间复杂度随数据规模 $n$ 增大的渐进增速。

举个空间复杂度为 $O(1)$ 的例子：

# O(1)，每次循环都只改变原有变量值
def o1(n):
    count = 0
    for i in range(n):
        count += i
    return count

如上面的代码，运行函数只新开辟了 count 这个变量，而循环并没有分配新的空间给变量，只是在原有数的基础上进行修改。当然，辅助变量 i 也算，但是根据估算规则，$O(2)$最后也等价于 $O(1)$。

此外，还有种常见的操作叫做递归，即函数自己调用自己。如下面空间复杂度为 $O(n)$ 的递归例子：

def sum_(n):
    if n == 0:
        return n # 递归一定要有的中断程序
    return n+sum_(n-1)

假设 $n=10$，当计算 $sum(10)$ 的时候，需要先计算 $sum(9)$，计算 $sum(9)$ 需要先计算 $sum(8)$…在整个递归调用过程中，被调用的函数依次被压入到系统栈中（先进后计算），而这些一层层的调用状态都需要占用一定空间。换言之，递归的空间复杂度取决于递归的深度。