力扣日记1.21-【回溯算法篇】77. 组合

news2024/10/2 22:25:15

力扣日记：【回溯算法篇】77. 组合

日期：2023.1.21
参考：代码随想录、力扣
终于结束二叉树了！听说回溯篇也是个大头，不知道这一篇得持续多久了……

77. 组合

题目描述

难度：中等

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按任何顺序返回答案。

示例 1：

输入：n = 4, k = 2
输出：
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]

示例 2：

输入：n = 1, k = 1
输出：[[1]]

提示：

1 <= n <= 20
1 <= k <= n

题解

class Solution {
#define SOLUTION 2
public:
#if SOLUTION == 1
    // 定义两个全局变量
    vector<vector<int>> result; // 存放结果集
    vector<int> path;   // 存放当前组合

    // 转换为树结构，树的宽度为当前集合长度(用for循环横向遍历)，树的深度为递归层数(组合个数k)
    vector<vector<int>> combine(int n, int k) {
        backtracking(n, k, 1);
        return result;
    }
    
    // 回溯三部曲
    // 1. 返回值为void，参数为原参数n、k以及表示当前集合开始遍历的起始位置
    void backtracking(int n, int k, int startindex) {
        // 2. 终止条件
        if (path.size() == k) { // 当前组合(大小)已满足条件
            // 存放结果
            result.push_back(path);
            return;
        }
        // 3. 回溯逻辑
        // for 循环横向遍历当前集合
        for (int i = startindex; i <= n; i++) { // index:[1, n]
            // 处理节点
            path.push_back(i);
            // 递归
            backtracking(n, k, i+1);    // 下一次从i+1开始遍历
            // 回溯，撤销处理节点
            path.pop_back();
        }
    }
#elif SOLUTION == 2 // 考虑剪枝优化
    // 剪枝优化主要体现在 for 循环横向遍历处
    // 如果剩余可遍历(取值)的元素数量不足以达到组合长度，则没有必要遍历
    // 即当前路径长度 path.size() + x >= k, 其中x为剩余可遍历的元素个数 x = n - startindex + 1(加1因为是左闭)
    // 所以startindex(即for中的i) 需 <= path.size() + n + 1 - k
    
    // 定义两个全局变量
    vector<vector<int>> result; // 存放结果集
    vector<int> path;   // 存放当前组合

    // 转换为树结构，树的宽度为当前集合长度(用for循环横向遍历)，树的深度为递归层数(组合个数k)
    vector<vector<int>> combine(int n, int k) {
        backtracking(n, k, 1);
        return result;
    }
    
    // 回溯三部曲
    // 1. 返回值为void，参数为原参数n、k以及表示当前集合开始遍历的起始位置
    void backtracking(int n, int k, int startindex) {
        // 2. 终止条件
        if (path.size() == k) { // 当前组合(大小)已满足条件
            // 存放结果
            result.push_back(path);
            return;
        }
        // 3. 回溯逻辑
        // for 循环横向遍历当前集合
        for (int i = startindex; i <= path.size() + n + 1 - k; i++) { // 剪枝优化
            // 处理节点
            path.push_back(i);
            // 递归
            backtracking(n, k, i+1);    // 下一次从i+1开始遍历
            // 回溯，撤销处理节点
            path.pop_back();
        }
    }
#endif
};

复杂度

时间复杂度：
空间复杂度：

思路总结

回溯算法理论基础

回溯算法模板框架：

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

将组合问题抽象为树形结构（N叉树）：

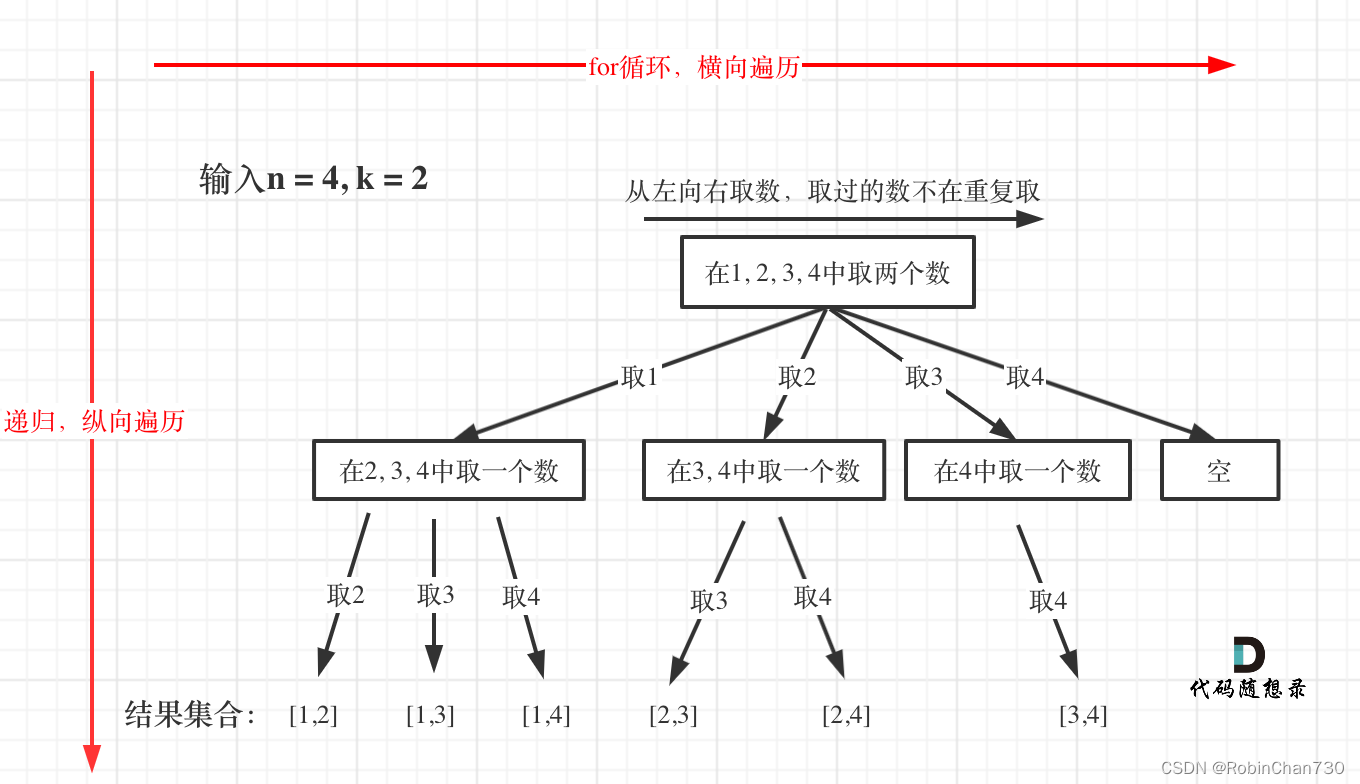
每个框即为每层递归的for循环，取值即为处理节点，最下面即为达到组合长度（终止条件）后存放结果
回溯法三部曲：
- 递归函数的返回值以及参数：
  - 为了简化参数，分别为存放整体结果集和单一组合定义两个全局变量，result和path；
  - 返回值一定为void，传递参数除了原始参数n和k，还要加一个startindex，用来记录本层递归的中，集合从哪里开始遍历
- 终止条件：当前组合(大小)已满足条件
  - 此时将组合保存进结果集
- 单层搜索的过程：
  - for 循环横向遍历当前集合（从startindex开始遍历）：
    - 首先处理节点（即将当前值放入path）
    - 接着进行递归（起始位置要+1）
    - 再是回溯（即撤销处理节点，将值弹出）
关于剪枝优化：
- 剪枝优化主要体现在 for 循环横向遍历处：
  - 如果剩余可遍历(取值)的元素数量不足以达到组合长度，则没有必要继续遍历
  - 即当前路径长度 path.size() + x >= k, 其中x为剩余可遍历的元素个数 x = n - startindex + 1(加1因为是左闭)
  - 所以startindex(即for中的i) 需 <= path.size() + n + 1 - k
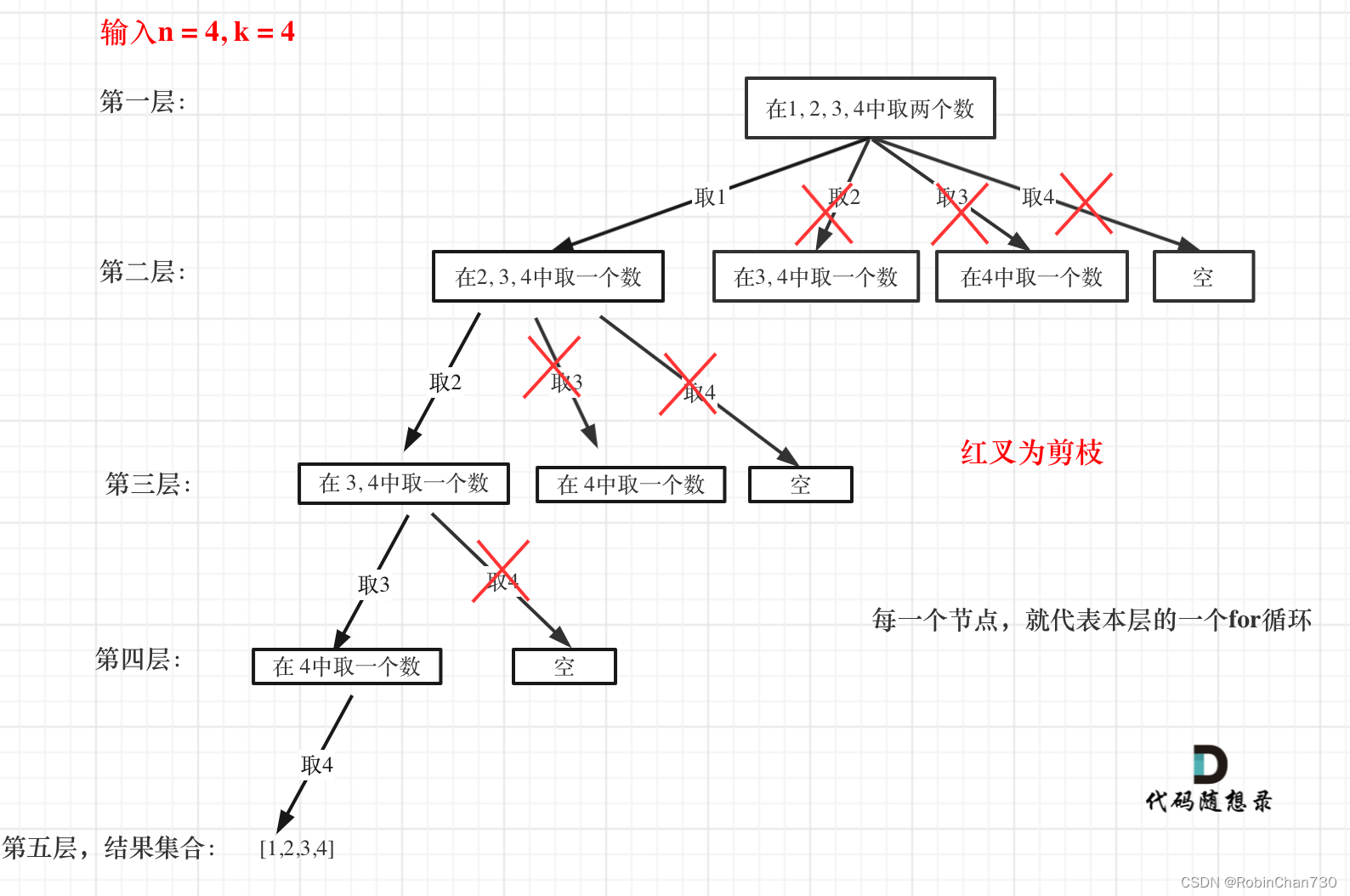
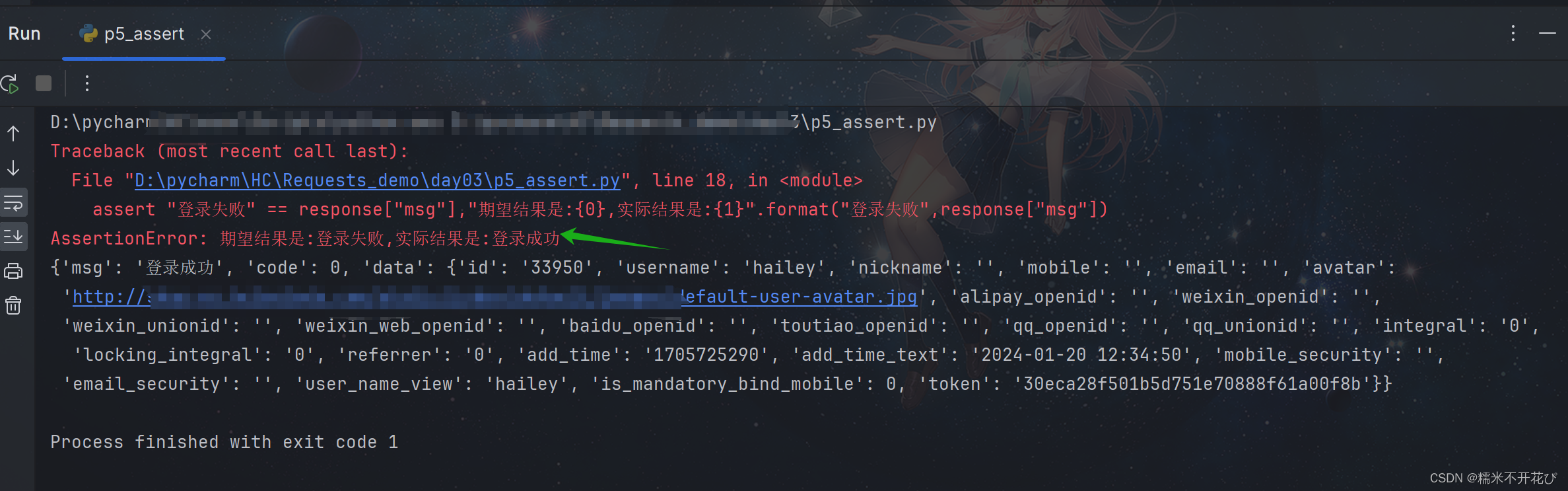
- 对于原来的不剪枝的情况，会在遍历到叶子节点（即for循环遍历完后）结束当前层递归，但由于未达到组合长度，所以在递归中不会添加到结果集。