1.问题描述

给你一棵二叉树的根节点，返回该树的直径 。

二叉树的 直径 是指树中任意两个节点之间最长路径的长度 。这条路径可能经过也可能不经过根节点 root 。

两节点之间路径的长度由它们之间边数表示。

示例 1：

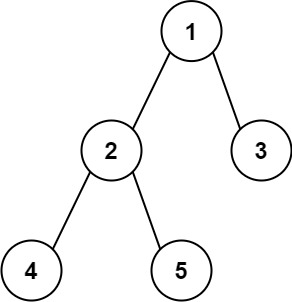
输入：root = [1,2,3,4,5]
输出：3
解释：3 ，取路径 [4,2,1,3] 或 [5,2,1,3] 的长度。

示例 2：

输入：root = [1,2]
输出：1

2.难度等级

Easy。

3.热门指数

★★★★☆

4.解题思路

可以深度优先搜索最长路径。

遍历每个结点作为根结点的最长路径上的结点数，其最长路径结点数等于其左子树与右子树高度和加 1。

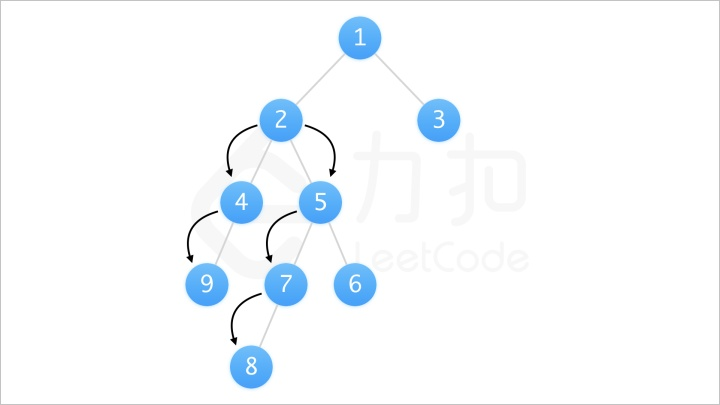
如图我们可以知道路径 [9, 4, 2, 5, 7, 8] 可以被看作以 2 为根，从其左子树向下遍历的路径 [2, 4, 9] 和从其右子树向下遍历的路径 [2, 5, 7, 8] 拼接得到。

所以解决该题需要先知道如何求解二叉树的高度。

如果我们知道了左子树和右子树的最大深度 l 和 r，那么该二叉树的最大深度即为：max(l,r)+1。

而左子树和右子树的最大深度又可以以同样的方式进行计算。因此我们可以用「深度优先搜索」的方法来计算二叉树的最大深度。具体而言，在计算当前二叉树的最大深度时，可以先递归计算出其左子树和右子树的最大深度，然后在 O(1) 时间内计算出当前二叉树的最大深度。递归在访问到空节点时退出。

知道了如何求解二叉树的高度之后，那么在递归搜索过程中记录当前结点作为根结点的最长路径。该最长路径就是整个二叉树的最长路径。

注意，题目要求的是最长路径上的边数，而不是结点数，所以最后返回时要减一。

时间复杂度： O(n)，其中 n 为二叉树的结点数，即遍历一棵二叉树的时间复杂度，每个结点只被访问一次。

空间复杂度： 递归函数分配栈空间为 O(logn)，即二叉树的高度。

下面以 Golang 为例给出实现。

var path int

func height(node *TreeNode) int {
	if node == nil {
		return 0
	}
	lh := height(node.Left)
	rh := height(node.Right)

	if lh+rh+1 > path {
		path = lh + rh + 1
	}
	if lh > rh {
		return lh + 1
	}
	return rh + 1
}

func diameterOfBinaryTree(root *TreeNode) int {
	path = 0
	height(root)
	return path - 1
}

---

参考文献

543. 二叉树的直径- LeetCode