题目描述

669.修剪二叉搜索树

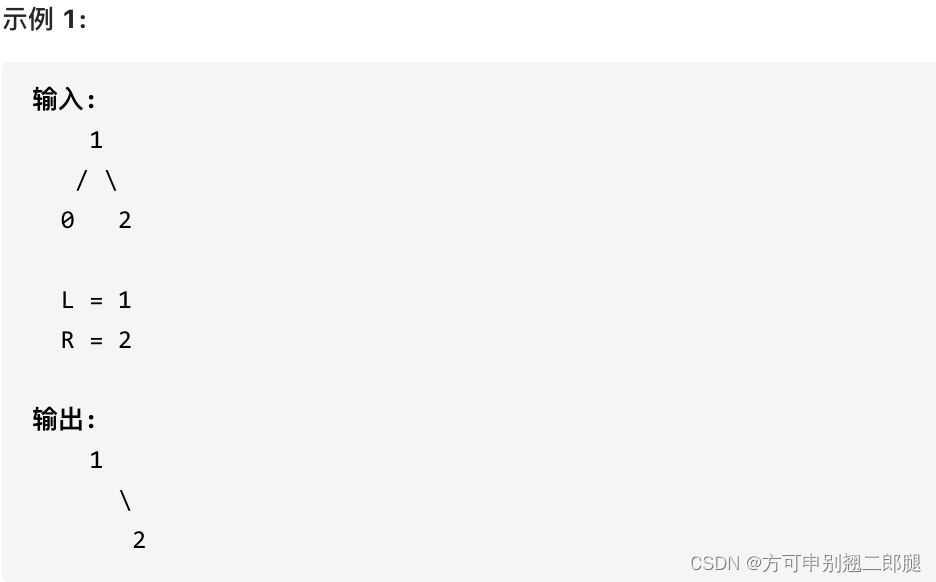
给定一个二叉搜索树，同时给定最小边界 L 和最大边界 R。通过修剪二叉搜索树，使得所有节点的值在[L, R]中 (R>=L) 。你可能需要改变树的根节点，所以结果应当返回修剪好的二叉搜索树的新的根节点。

解题思路

递归法，当遇到root->val < low || root->val > high 的时候直接return NULL，但是[1, 3]区间在二叉搜索树的中可不是单纯的节点3和左孩子节点0就决定的，还要考虑节点0的右子树。

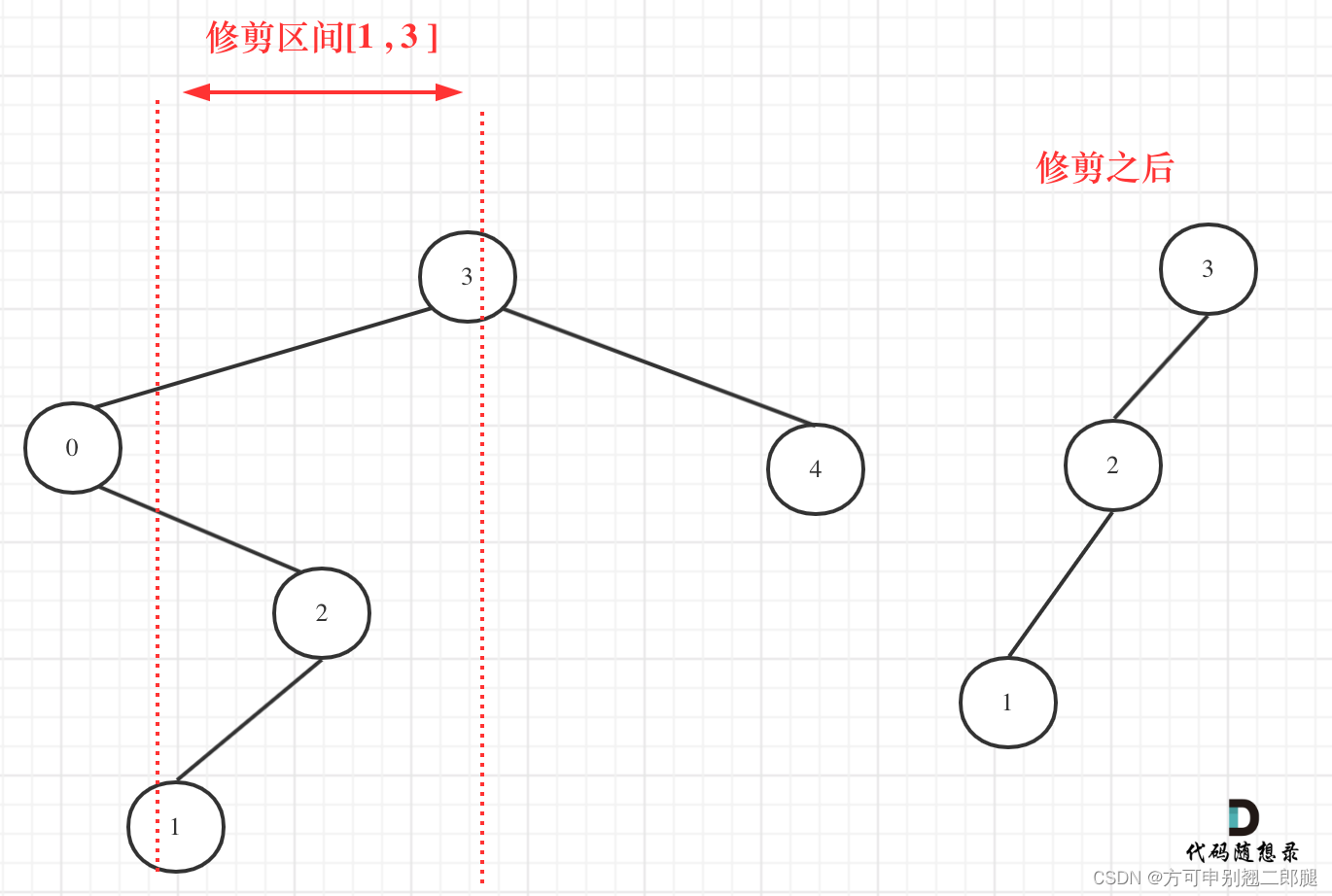
在上图中我们发现节点0并不符合区间要求，那么将节点0的右孩子 节点2 直接赋给 节点3的左孩子就可以了（就是把节点0从二叉树中移除），如图：

递归三部曲

1. 确定递归函数的参数和返回值
   参数：根节点。以及两个值low、high
   返回值：利用返回值来移除节点，TreeNode*

   TreeNode* trimBST(TreeNode* root, int low, int high)
   

2. 确定递归函数的终止条件
   遇到空节点返回。

   if(root == nullptr) return nullptr;
   

3. 确定单层递归的逻辑
   如果root（当前节点）的元素小于low的数值，那么应该递归右子树，并返回右子树符合条件的头节点：

   if (root->val < low) {
   	TreeNode* right = trimBST(root->right, low, high);// 寻找符合区间[low, high]的节点
   	return right;
   }
   

   如果root（当前节点）的元素大于high的，那么应该递归左子树，并返回左子树符合条件的头节点：

   if (root->val > high) [
   	TreeNode* left = rimBST(root->left, low, high); // 寻找符合区间[low, high]的节点
   	return left;
   }
   

   接下来要将下一层处理完左子树的结果赋给root->left，处理完右子树的结果赋给root->right。

   最后返回root节点，代码如下：

   root->left = trimBST(root->left, low, high); // root->left接入符合条件的左孩子
   root->right = trimBST(roo->right, low ,high); // rot->right接入符合条件的右孩子
   return root;
   

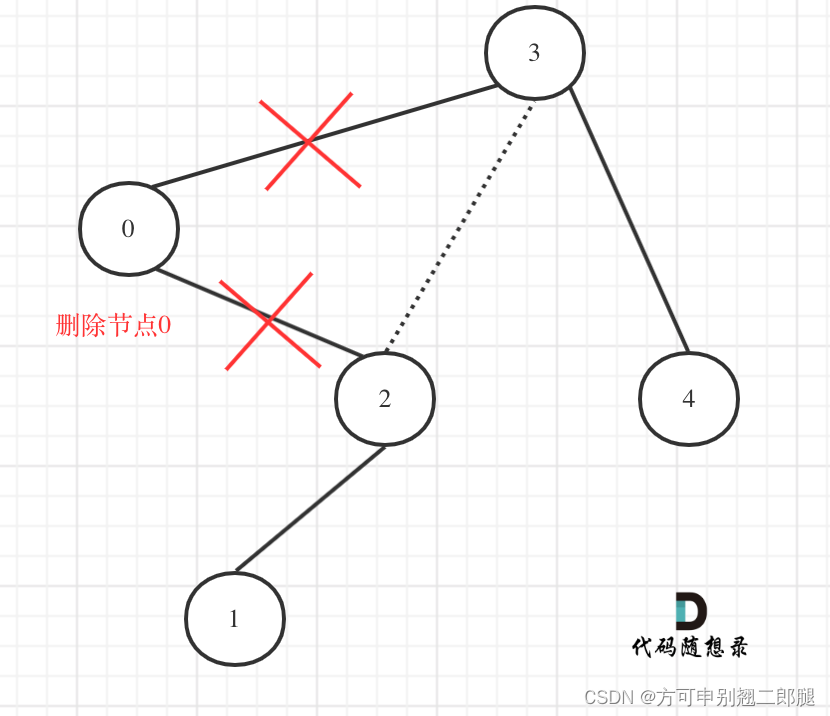
针对下图的情况，移除多余节点的逻辑如下：

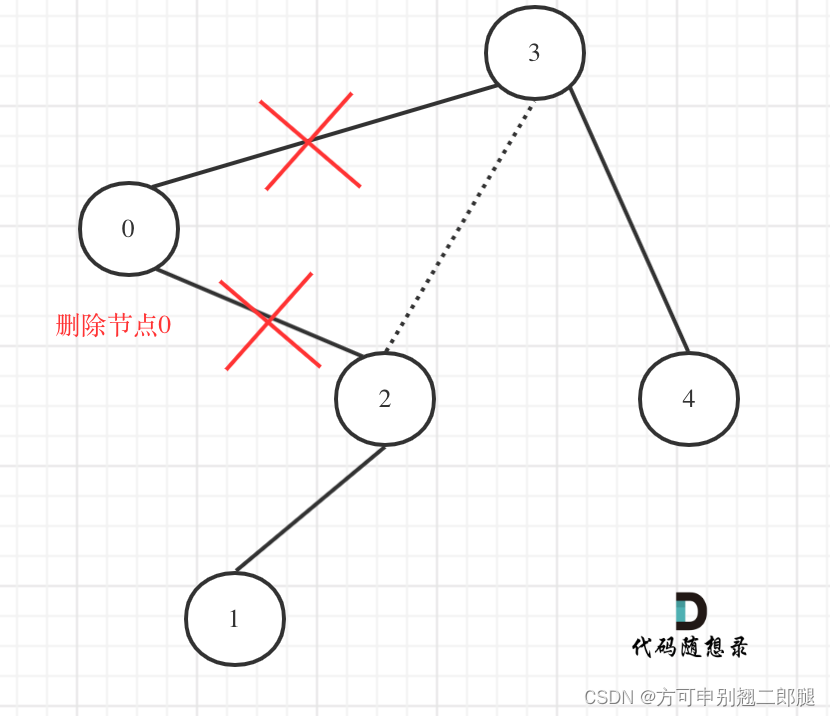
这一步相当于将要移除的节点（节点0）的右孩子（节点2）返回给上一层

	if (root->val < low) {
		TreeNode* right = trimBST(root->right, low, high);  // 寻找符合区间[low, high]的节点
		return right;
	}

如下代码相当于节点3的左孩子把下一层返回的节点0的右孩子（节点2）接住。

root->left = trimBST(root->left, low, high);

此时节点3的左孩子就变成了节点2，将节点0从二叉树中移除了。

代码实现

class Solution {
public:
	TreeNode* trimBST(TreeNode* root, int low, int high) {
		if (root == nullptr) return nullptr;
		
		if (root->val < low) {
			TreeNode* right = trimBST(root->right, low, high);
			return right;
		}
		
		if (root->val > high) {
			TreeNode* left = trimBST(root-<left, low, high);
			return left;
		}
		
		root->left = trimBST(root->left, low, high);
		root->right = trimBST(root->right, low, high);
		return root;
	}
};