二叉树(Binary Tree)的基础

1、树的概念

1、树的概念

树是一种非线性的数据结构，是由n（n>=0）个有限结点组成一个具有层次关系的集合，将它称为树，是因为在形状上像一颗倒着的树，如下图所示就是一颗二叉树。

可以发现，对于树中的根节点，没有前驱节点，有多个后驱节点；对于其他节点，有一个前驱节点，有或没有后驱节点。这就是它属于非线性结构的原因，节点的对应关系是一对多并且子树之间不相交，可以用此特点来判断树与非树。

2、树元素的基本概念

结点的度：一个结点含有子树的个数称为该结点的度
树的度：一棵树中，所有结点度的最大值称为树的度
叶子结点或终端结点：度为0的结点称为叶结点
双亲结点或父结点：若一个结点含有子结点，则这个结点称为其子结点的父结点；
孩子结点或子结点：一个结点含有的子树的根结点称为该结点的子结点
根结点：一棵树中，没有双亲结点的结点
树的高度或深度：树中结点的最大层次

3、树的表示形式

我们可以发现，如果要构建出这个结点，必须要有三部分：结点的值、结点的左孩子引用、结点的右孩子引用。我们可以借助类来实现结点的实例化。

class TreeNode {
	public int val;//结点的值
	public TreeNode left;//结点的左孩子引用
	public TreeNode right;//结点的右孩子引用
}

2、二叉树

1、二叉树的概念

一棵二叉树是结点的一个有限集合，该集合：

1. 或者为空
2. 或者是由一个根节点加上两棵别称为左子树和右子树的二叉树组成
   

从二叉树的概念中我们可以发现：

1. 二叉树不存在度大于2的结点
2. 二叉树的子树有左右之分，次序不能颠倒，因此二叉树是有序树

2、特殊的二叉树

1、满二叉树：每层的结点数都达到最大值的二叉树，结点总数为2^k-1
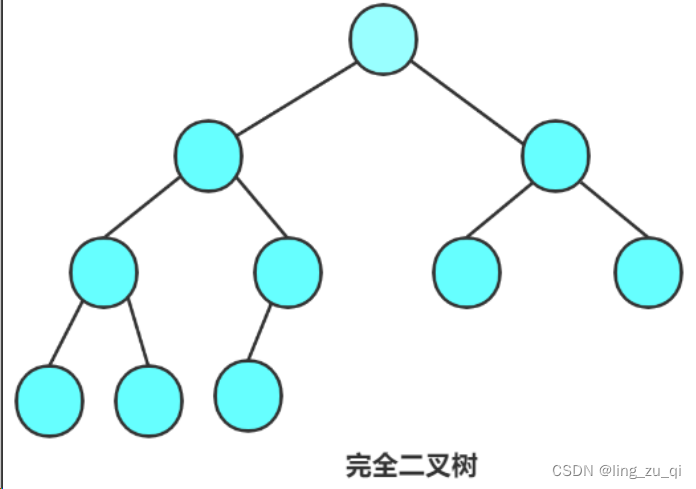
2. 完全二叉树:从左到右，从上到下给二叉树的结点编号遍历，如果二叉树在遇到空结点之后的结点都为空，就是完全二叉树。满二叉树是完全二叉树的一种特例。

3、二叉树的性质

1. 若规定根结点的层数为1，则一棵非空二叉树的第i层上最多有 (i>0)个结点
2. 若规定只有根结点的二叉树的深度为1，则深度为K的二叉树的最大结点数是 (k>=0)
3. 对任何一棵二叉树, 如果其叶结点个数为 n0, 度为2的非叶结点个数为 n2,则有n0＝n2＋1
4. 具有n个结点的完全二叉树的深度k为 log2（n+1）上取整
5. 对于具有n个结点的完全二叉树，如果按照从上至下从左至右的顺序对所有节点从0开始编号，则对于序号为i的结点有：
   若i>0，双亲序号：(i-1)/2；i=0，i为根结点编号，无双亲结点
   若2i+1<n，左孩子序号：2i+1，否则无左孩子
   若2i+2<n，右孩子序号：2i+2，否则无右孩子

4、二叉树的遍历

二叉树的遍历常常采用递归解决，原因是每一个结点的结构相同，处理每一个结点的方式相同，因此可以使用递归来解决重复的子问题。

1、前序遍历

前序遍历的顺序为根节点-左孩子结点-右孩子结点。其中对于左孩子结点也使用相同的遍历顺序，直到遇见空结点为止。利用下图进行举例。
#表示空结点
A-B-D-#，遇到空结点，递进过程结束，回归开始。回到D向右树继续递进，D-#，遇到空结点，递进过程结束，回归开始。回到B向右树继续递进，B-#，遇到空结点，递进过程结束，回归开始。回到A向右树继续递进…
所以前序遍历的结果为：ABDCE

2、中序遍历

中序遍历的顺序为左孩子结点-根节点-右孩子结点。
对于A，先遍历B,对于B先遍历D，D-B-A；对于C，先遍历E，A-E-C
所以中序遍历的结果为：DBAEC

3、后序遍历

后序遍历的顺序为左孩子结点-右孩子结点-根节点。

对于A，先遍历B，对于B，先遍历D，D-B；再遍历C，对于C，先遍历E，E-C
所以后序遍历的结果为：DBECA

三种遍历代码实现（递归）

//前序遍历
public void preOrder(TreeNode root) {
	if(root==null) {
		return;
	}
	System.out.print(root.val+" ");
	preOrder(root.left);
	preOrder(root.right);
}

//中序遍历
public void inOrder(TreeNode root) {
	if(root==null) {
		return;
	}
	inOrder(root.left);
	System.out.print(root.val+" ");
	inOrder(root.right);
}

//后序遍历
public void postOrder(TreeNode root) {
	if(root==null) {
		return;
	}
	postOrder(root.left);
	postOrder(root.right);
	System.out.print(root.val+" ");
}

三种递归方式实质上都是利用了子问题的思想，将左右孩子拆出来作为新的树，利用同样的方式处理，十分容易理解。